数据结构与算法

第一部分 算法简单概念

　　算法概念

　　复习：递归

　　时间复杂度

　　空间复杂度

什么是算法？

　　算法（Algrithm）:一个计算过程，解决问题的方法

 

 复习：递归

递归的两个特点：

　　　　（1）、调用自身

　　　　　(2)、结束条件

简单的几个函数：

def func1(x):
    print(x)
    func1(x-1)

def func2(x):
    if x>0:
        print(x)
        print(x+1)

def func3(x):
    if x>0:
        print(x)
        func3(x-1)

def func4(x):
       if x>0:
            func4(x-1)
            print(x)

 

时间复杂度

　　如下代码：判断其时间复杂度

print("hello World")


for i in range(n):
    print("hello world")

for i in range(n):
    for j in range(n):
        print("hello world")

for i in range(n):
    for j in rnage(n):
        for k in range(n):
            print("Hello World")

 

以上四组代码，那组运行时间最短？

用什么方式来体现代码（算法）运行的快慢？

时间复杂度：用来评估算法运行效率的一个介质。

上述的时间复杂度分别如下：一般肉眼观察，循环了几次，print了几次。

 

再看以下代码例子：

 

 

 类比生活中的一些时间例子，估计时间：不是一个确切的数而是个约数

 

继续推算时间复杂度的其他表示方法？

 综上，总结一下时间复杂度

"""

时间复杂度是用来估计算法运行时间的一个式子（单位）。
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度（按效率排序）
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
不常见的时间复杂度（看看就好）
O(n!) O(2n) O(nn) …
如何一眼判断时间复杂度？
循环减半的过程O(logn)
几次循环就是n的几次方的复杂度

"""

补充：为什么python中的b+树，二叉树查询速度灰快些？

　　从时间复杂度的角度理解，因为它的时间复杂度仅次于O(1)

数据库添加B-树索引，查询就快。那么为啥添加索引就快？

B-树索引的内部结构如下：

理解下图就明白了

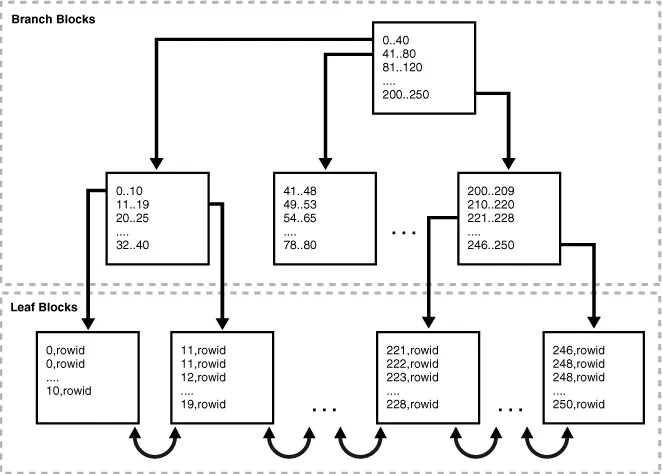
B-树索引有两种类型的块： 用于查找的分支块（Branch Blocks）和用于存储值的叶块（Leaf Blocks）。
B-树索引的上层分支块包含指向下层索引块的索引数据。从结构上来说就像树一样，分支块就是树干树枝，而叶子就是叶块。
但是和树有区别的是B-树索引是平衡的，所有叶块都自动处于相同的深度。
因此，在索引中从任意位置检索任意记录需要的时间基本上是相同的。可以理解为，如果走索引从中查询一条数据，那么我查找1W条数据和查询100w条数据的速度是一样的。
最底层的叶块包含每个被索引的数据值，和一个相应的用来定位实际行的rowid。根据分支块，找到被索引的数据值，再找到对应的rowid，再从rowid取出对应的数据，就起到了快速查找数据的目的。

空间复杂度　

空间复杂度：用来评估算法内存占用大小的一个式子。
“空间换时间”，更多的是涉及硬件性能有关，如内存，硬盘，cpu等。

常见的算法

　　排序算法是《数据结构与算法》中最基本的算法之一。

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

# 1.0 十大经典排序算法
# 1.1 冒泡排序
# 1.2 选择排序
# 1.3 插入排序
# 1.4 希尔排序
# 1.5 归并排序
# 1.6 快速排序
# 1.7 堆排序
# 1.8 计数排序
# 1.9 桶排序
# 1.10 基数排序

 

 

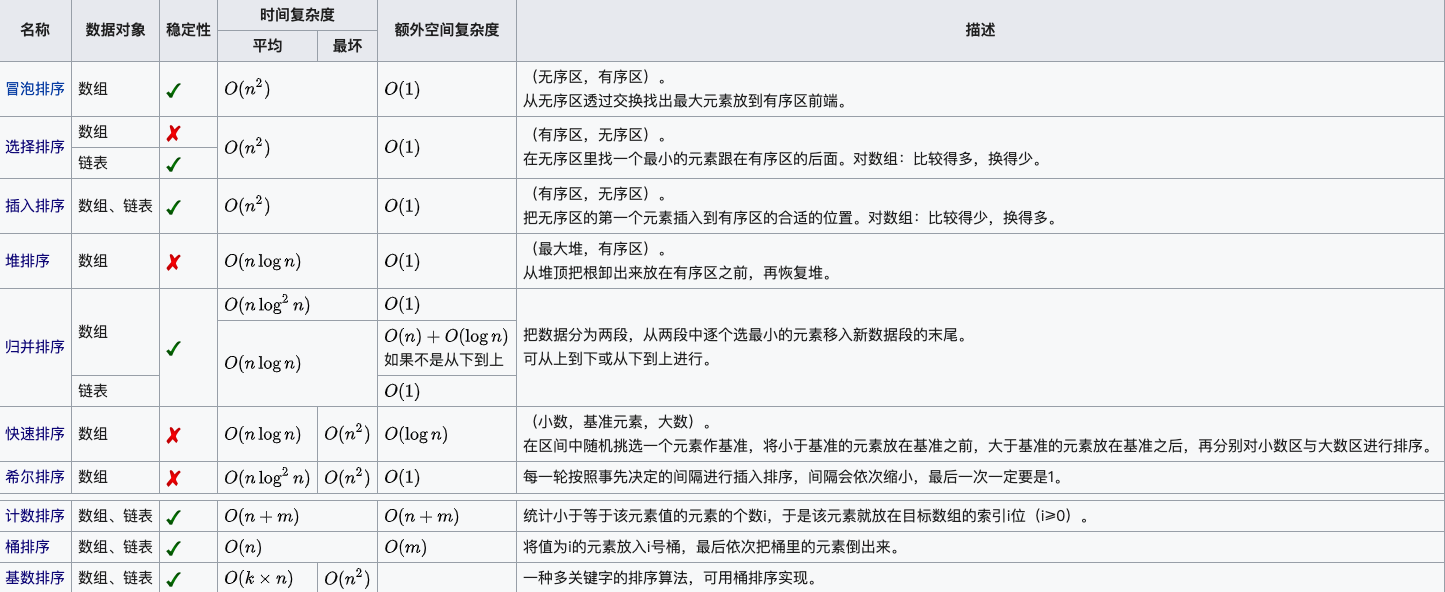
关于时间复杂度

　平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

n：数据规模
k："桶"的个数
In-place：占用常数内存，不占用额外内存
Out-place：占用额外内存
稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

 

1、列表查找

列表查找：从列表中查找指定元素
输入：列表、待查找元素
输出：元素下标或未查找到元素

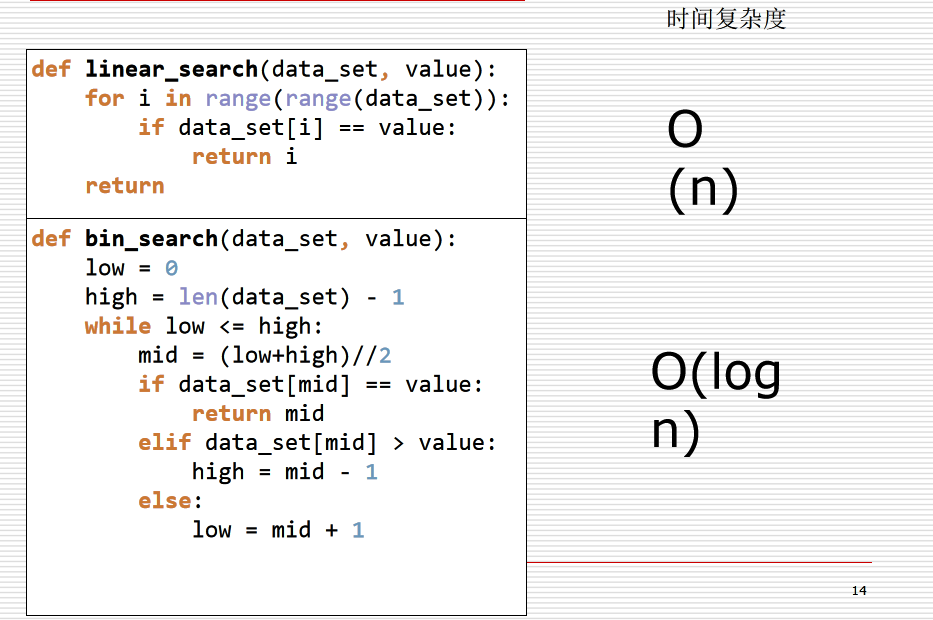
顺序查找
从列表第一个元素开始，顺序进行搜索，直到找到为止。
二分查找
从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

 

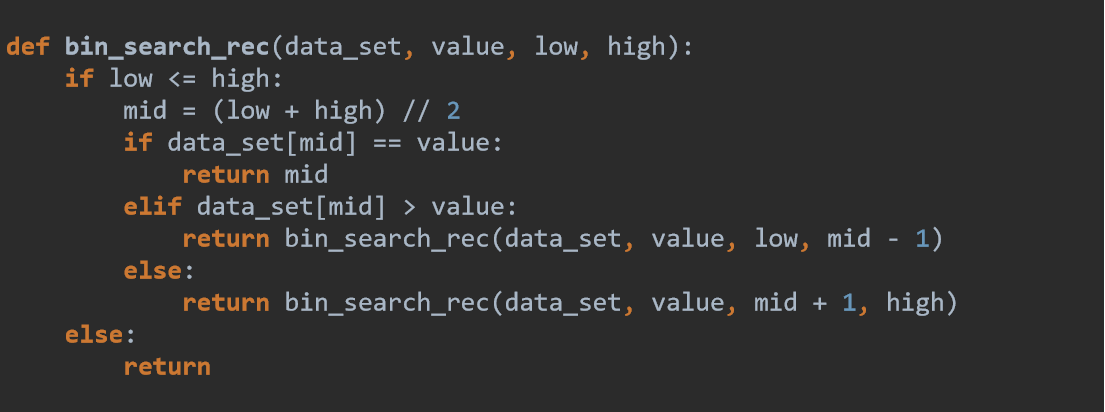
列表查找

 

 递归版的二分法查找

 

 

 2、冒泡排序思路

　　首先，列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数……
会发生什么？

1. 算法步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

2. 动图演示

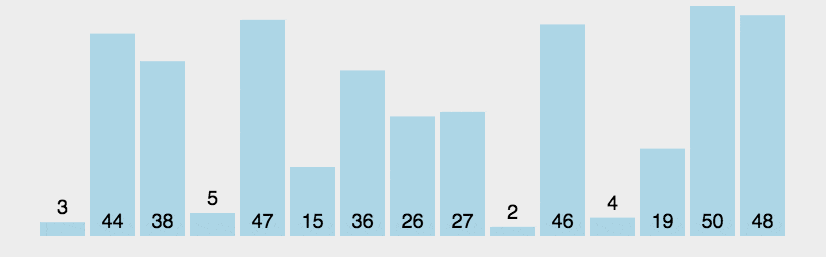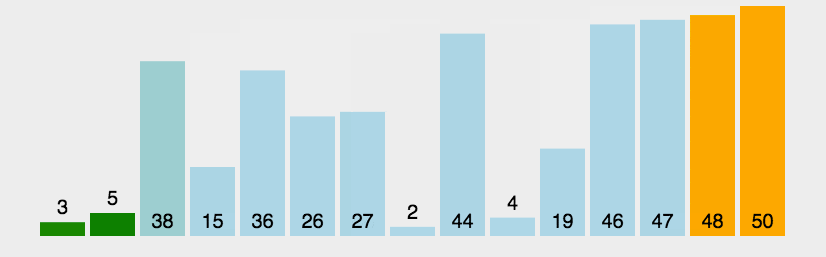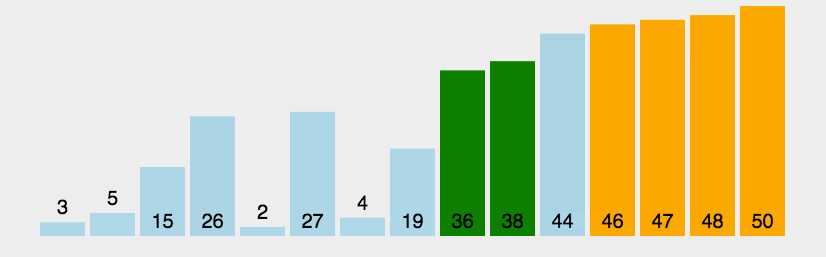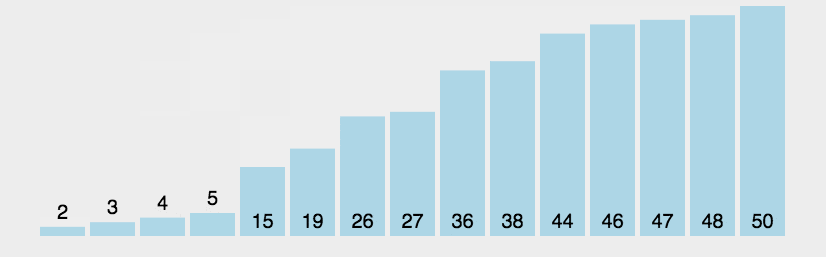
python代码实现

#### 冒泡排序  (************************)
### 时间复杂度：O(n^2)
def Bubble_sort(li):
    for i in range(len(li)-1): # 第一趟是循环遍历
        for j in range(len(li)-1-i): # 内层循环是两两之间进行比较，取出较大的数
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
li=[1,2,3,5,8,4,9,10,12]
Bubble_sort(li)
print(li)

 

3、选择排序思路　

一趟遍历记录最小的数，放到第一个位置；
再一趟遍历记录剩余列表中最小的数，继续放置；
……


问题是：怎么选出最小的数？


代码关键点：
无序区
最小数的位置

 

　　选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。

唯一的好处可能就是不占用额外的内存空间了吧。

1. 算法步骤

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。

再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

重复第二步，直到所有元素均排序完毕。

2. 动图演示

代码实现：

#### 选择排序
#### 时间复杂度：O(n^2)
def select_sort(li):
    for i in range(len(li)):
        minLoc = i ###i = 0
        for j in range(i+1, len(li)):
            if li[j] < li[minLoc]:
                li[j], li[minLoc] = li[minLoc], li[j],10
li=[2,5,4,6,8,9,14,7]
select_sort(li)
print(li)

 

4、插入排序思路

列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。

 

插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。

插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序和冒泡排序一样，也有一种优化算法，叫做拆半插入。

1. 算法步骤

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

2. 动图演示

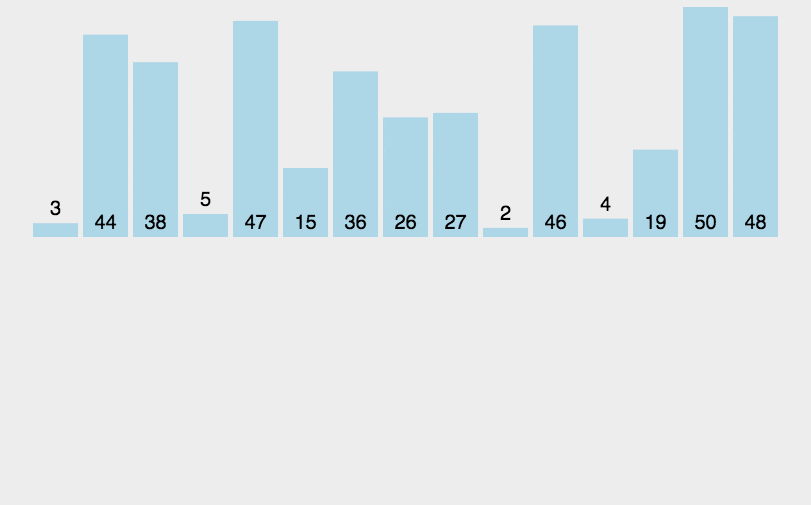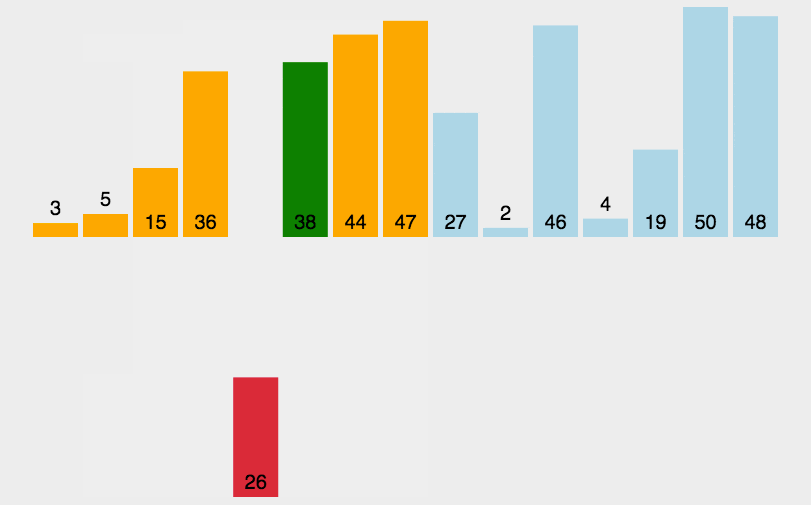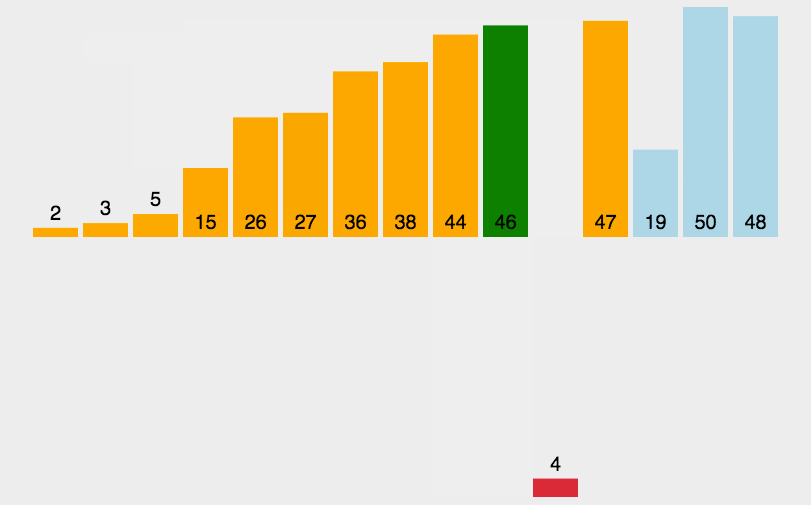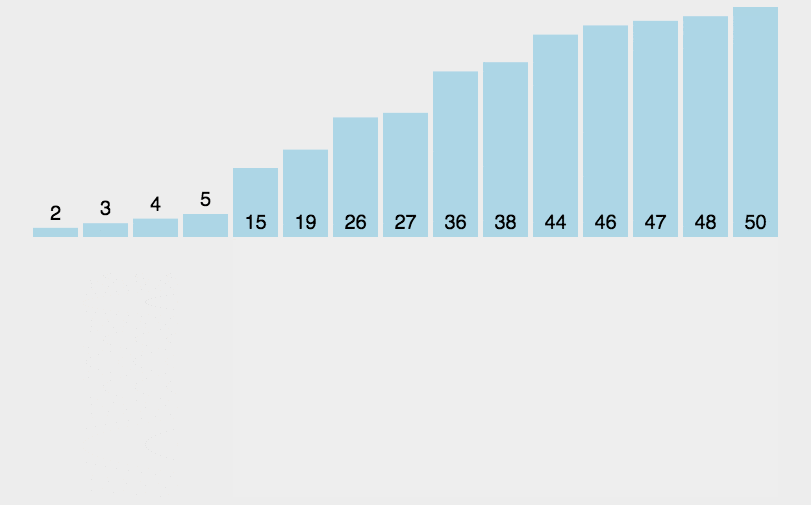
代码实现：

##### 插入排序
#### 时间复杂度： O(n^2)
def insert_sort(li):
    for i in range(1, len(li)):
        tmp = li[i]
        j = i - 1
        while j >=0 and li[j] > tmp:
            li[j+1] = li[j]
            j = j - 1
        li[j+1] = tmp

li = [1,2,5,7,12,23,15,56,21,45]
insert_sort(li)
print(li)

 

 

5、 快速排序思路

快速排序：快
好写的排序算法里最快的
快的排序算法里最好写的

 

1. 算法步骤

1、从数列中挑出一个元素，称为 "基准"（pivot）;

2、重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

3、递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

 2. 动图演示

 代码实现

def partition(li, left, right):
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:
            right = right - 1
        li[left] = li[right]
        while left < right and li[left] <= tmp:
            left = left + 1
        li[right] = li[left]
    li[left] = tmp

    return left

#### 快速排序
#### 时间复杂度：O(nlogn) 
def quick_sort(li, left, right):
    if left < right:
        mid = partition(li, left, right)
        quick_sort(li, left, mid-1)
        quick_sort(li, mid+1, right)

 6、计数排序

 算法的步骤如下：

（1）找出待排序的数组中最大和最小的元素
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

2. 动图演示

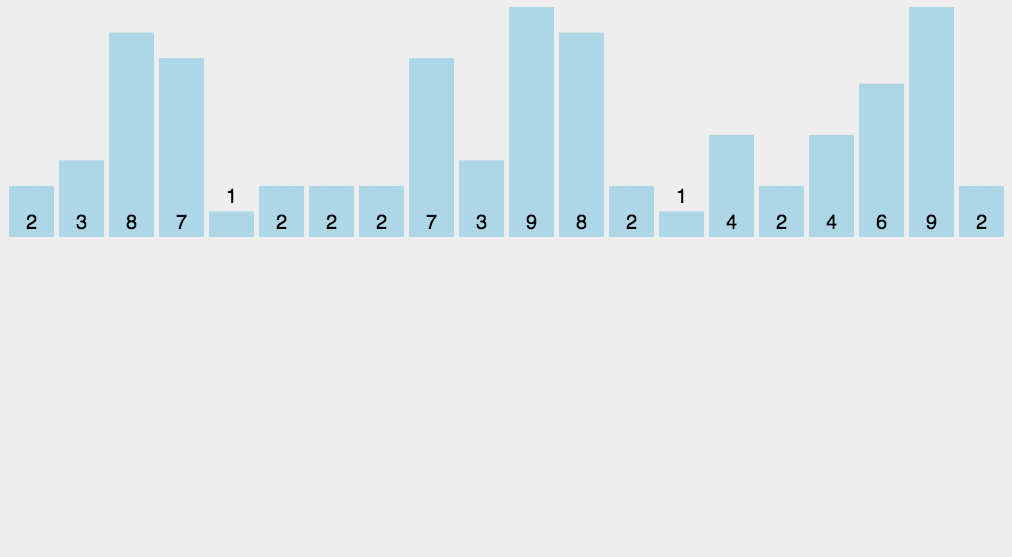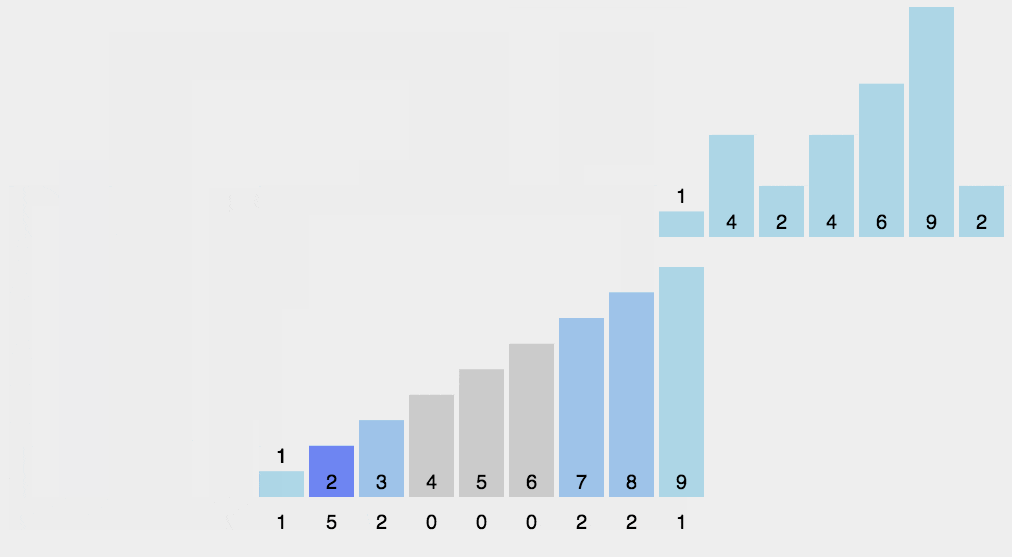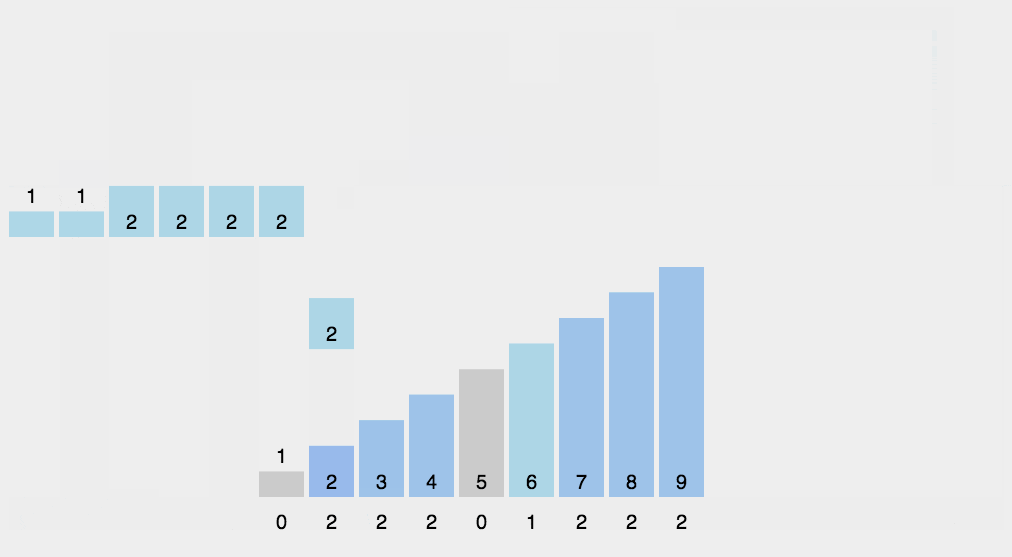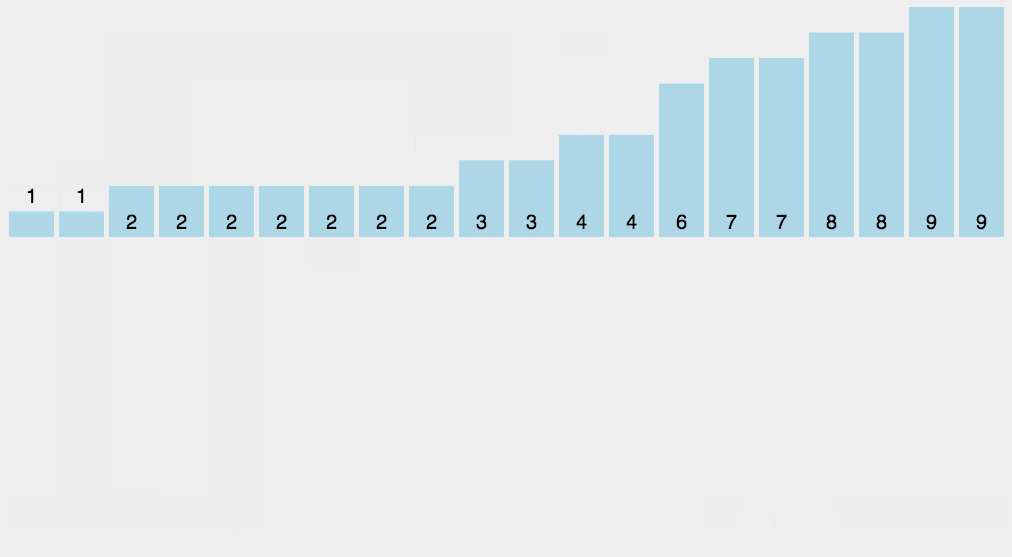
代码的实现：

# 创建一个列表，用来统计每个数出现的次数

#现在有一个列表，列表中的数范围都在0到100之间，
# 列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。

def count_sort(li,max_num):
    count = [0 for i in range(max_num+1)]
    for num in li:
        count[num] += 1
    i = 0
    for num,m in enumerate(count):
        for j in range(m):
            li[i] = num
            i += 1
li = [1,2,5,2,0,1,11,54,212,154,1,24,12,5,6,5,2,8,9,20,12,23,45,16]
count_sort(li,1000)
print(li)

 线性结构

　　把所有的节点用一根线串起来

数组和链表的区别

　　数组需要一块连续的内存空间来存储，对内存的要求比较高。如果我们申请一个 100MB 大小的数组，当内存中没有连续的、足够大的存储空间时，即便内存的剩余总可用空间大于 100MB，仍然会申请失败。 而链表恰恰相反，它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用，所以如果我们申请的是 100MB 大小的链表，根本不会有问题。

 

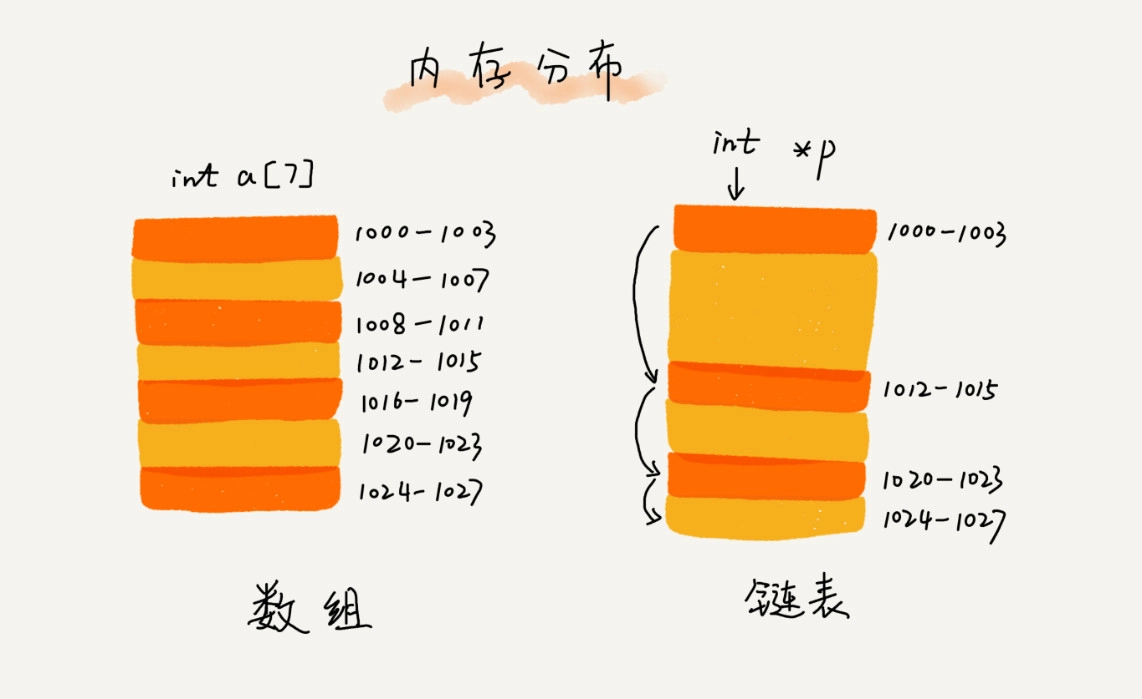
离散存储（链表）

 

 

推荐的学习书籍