简述差分隐私
差分隐私基础知识，不涉及深层理论。
引言：
差分隐私（就个人理解）是为了对抗差分攻击而引入的一种隐私保护的方案。试想一下，一个简易的相亲系统，数据库中存储了单身4人，已婚12人（别问我已婚为啥还要注册相亲系统，你没钱还喜欢逛淘宝呢），张三新注册了一个账号之后，单身变成了5人，已婚还是12人。明眼人一看就知道，张三是单身。这种造成的信息泄露就称为差分攻击。（还可以看一下数据重构攻击，这也是差分隐私为了克服攻击的一种）
主要参考以下视频，有兴趣可自行查看
差分隐私：原理、应用与展望 https://www.bilibili.com/video/BV1Tk4y117uA
差分隐私（一） Differential Privacy 简介 https://zhuanlan.zhihu.com/p/139114240
定义：
为保护数据集不会被某一个体的变化产生巨大的变化（或造成数据的泄露)，引入一种隐私保护方案：差分隐私保护。其定义如下：差分隐私（英语：differential privacy）是密码学中的一种手段，旨在提供一种当从统计数据库查询时，最大化数据查询的准确性，同时最大限度减少识别其记录的机会。（来自：Baidu）
而一切机器学习也好，隐私保护也罢，都离不开数学公式的支持，而差分隐私的数学公式为：
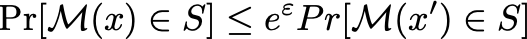
该函数来自于
The Algorithmic Foundations of Differential Privacy https://www.cis.upenn.edu/~aaroth/Papers/privacybook.pdf
倘若不好理解，可以把式子具体化，例如在一个数据集D中，查询一个信息，其结果可能返回0或其他值。D'表示，原D数据集中的某一个元素发生改变。例如，原相亲系统为D，在相亲系统中删除张三数据，数据集变成了D'，下式中的A表示一个算法（即采用何种差分隐私的算法）。
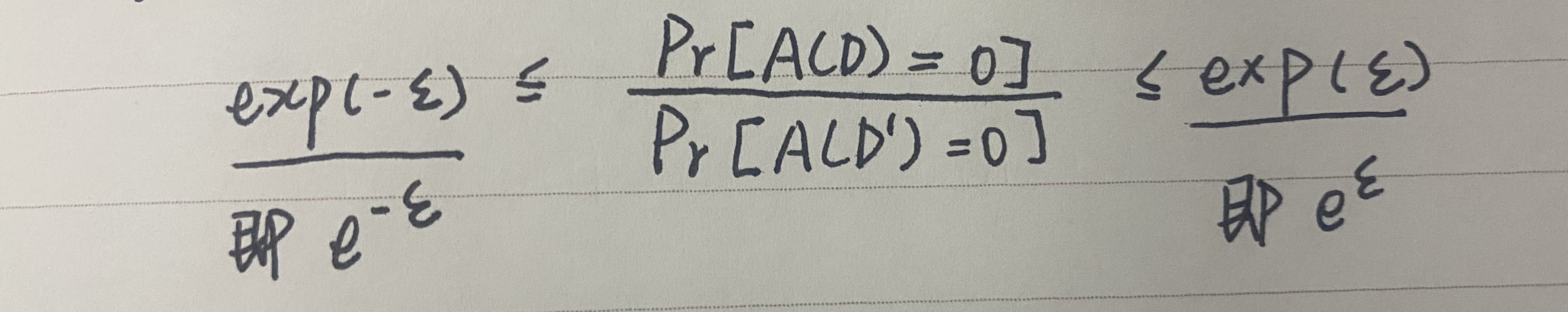
公式可以解释为：修改前数据库输出为0的概率和修改后数据库输出为0的概率，其值应该不小于exp（-ε），且不大于exp（ε）。而满足这个式子，我们称该A算法满足了ε-差分隐私。
不难得知，ε越小，对用户的数据保护要求越高。
几个指标
全局敏感度：其度量了在修改一个元组时（即某一条数据）查询结果的最大变化，可以用如下的公式进行表示：
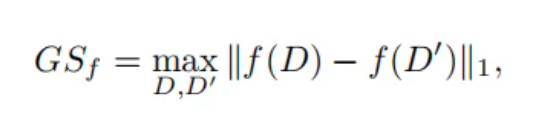
式中的||f(D)-f(D')||1,表示曼哈顿距离，可以理解为，将线段投影到坐标轴，可能获得两个线段或者一个线段一个点，将其值加起来就是曼哈顿距离(也成为出租车距离)。
可参考：https://baike.baidu.com/item/曼哈顿距离/743092
值得注意的是它独立于数据集，只和查询函数有关。譬如：在计数函数中，全局敏感度为1。而对于其他的函数，例如中值函数中，其全局敏感度可能是较大的一个值，举一个直观的例子，在下面的直方图表示中，其值最大为1
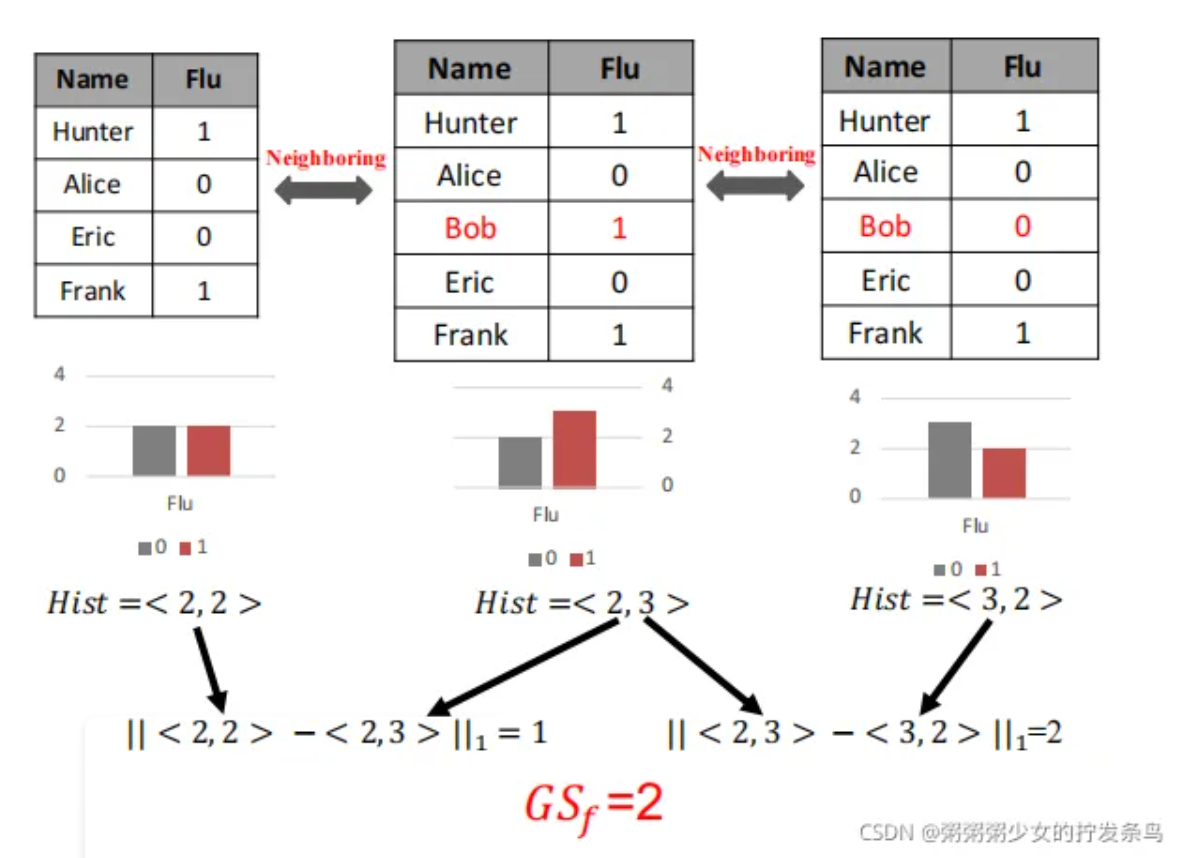
局部敏感度：当全局灵敏度较大时，必须向输出中添加大量的噪声，以实现差分隐私，这可能会严重损害数据效用。故我们引入局部敏感度来改善这个问题。
局部敏感度是在给定的数据集D和任意的临近数据集，故：局部敏感度由函数F及给定数据集D中获得具体数据共同决定，且局部敏感通常要比全局敏感度小的多。
这里自己也不是很懂，等懂了之后再补充上
有用的性质（随时补充）：
顺序合成：当有一些算法序列同时作用在一个数据集上是，最终的差分隐私预算（即ε）等于算法序列中虽有算法的预算和。即满足叠加原理。
平行合成：将一个数据集分成不用的集合，对不同的集合采取不同的算法进行保护，那么数据集最后的隐私代价为，各算法中ε最大的值。
经典算法：
1、拉普拉斯机制：
对我们的查询结果加入一个拉普拉斯噪声，即可有效的降低差分隐私攻击，加入的噪声可以用数学公式表示为：
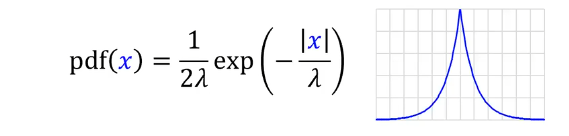
特别的，当λ设置为1/ε时，即可满足我们的ε-差分隐私的要求。
2、随机化回答：
系统收到的数据集并不一定都是真实的。试想一个这样的场景，对一个十分隐私的问题（eg：你是不是处？），用户不一定想给真实的答案，那么我们就可以引入随机化回答。其可以用下图来理解：
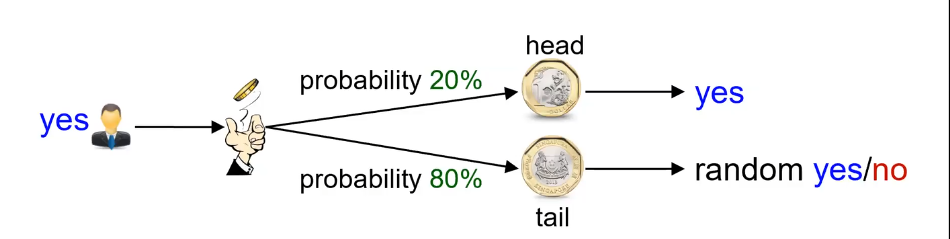
即用户诚实的回答yes，但是并不一定给出这个诚实的答案，他会投一个硬币，如果是正面（假设可能性是20%，当然这是不和常理的，但这并不影响我们分析问题），那么用户给出诚实的答案。但如果是反面（概率为80%）用户可能随机的给出yes/no（通常来说是一半的概率）。这样数据库中的信息无法推断出某一特定用户的信息，可能有人有疑问，那这些数据有什么用呢？其实，通过统计学的知识不难知道，我们倘若有8000人给出了yes，2000给出了no，那么一共有10000人，其中有80%的人给出的是随机答案，排除这些人，给出yes和no的人数分别为：1600和400，给出的是诚实的答案。
这样保护了用户的隐私，还得到了我们想要的统计结果。（偏差是不可避免的）
未完结，不定时更新
