记忆化搜索状态重叠

在做 LeetCode 309. 最佳买卖股票时机含冷冻期 时，写完递归超时后，企图用记忆化搜索优化，但是发现原本正确的结果变成错的了

Debug过程：

对于 [2,1,4] 这个用例，列出所有情况后发现最后一步的 not sell 和 buy 两个状态重叠了，导致记忆化错误

 

 

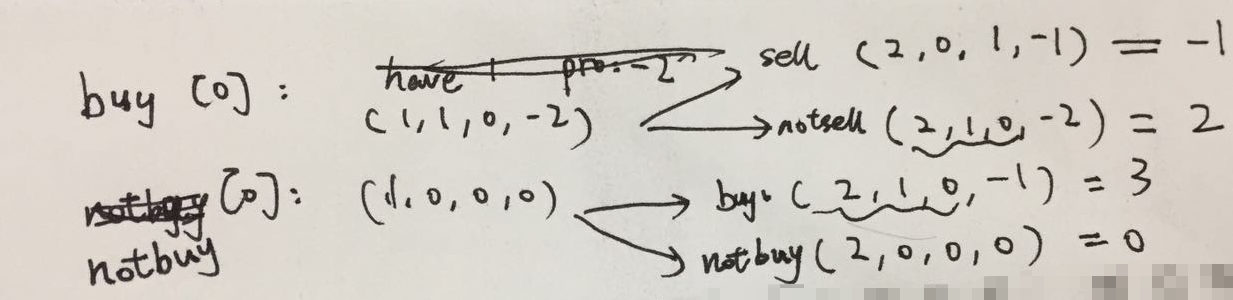
随后改为自顶向下的dp通过

 

查阅资料发现：https://www.cnblogs.com/zcy0917/p/9316487.html

---

 

记忆化搜索的适用范围

    根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关”的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。

也就是说，他的问题表达，不是单纯生成一个走步方案，而是生成一个走步方案的代价等，而且每走一步，在搜索树/图中生成一个新状态，都可以精确计算出到此为止的费用，也就是，可以分步计算，这样才可以套用已经得到的答案.

 

使用条件

• 对于一定状态有唯一相同的解，不应对于一个状态有多个解（解不相同）；
• 到达底层时可立即返回解，不应得出路径后才能计算解；
• 状态数量和规模应能够在有限数据结构中存储。

TIP

• 遵循无后效性原则；//某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响。
• 局限性：可十分简洁的优化为递归，即动态规划。
• 往往对于dfs才会使用记忆化，因为bfs并不会重复搜索到某一个状态，而一旦搜索到结果就是最优解，此时立即退出；

---

 

 

递归：

class Solution {
    int[] prices;

    public int iter(int idx, boolean have, boolean frozen, int profit){
        if (idx == prices.length - 1){
            if (have){
                profit += prices[prices.length - 1];
            }
            return profit;
        }

        if (frozen){

            return iter(idx + 1, have, false, profit);
        }

        if (have){
            int sell = iter(idx+1, false, true, profit + prices[idx]);
            int notsell = iter(idx+1, true, false, profit);
            return Math.max(sell, notsell);
        }else {
            int buy = iter(idx+1, true, false, profit - prices[idx]);
            int notbuy = iter(idx+1, false, false, profit);
            return Math.max(buy, notbuy);
        }
    }

    public int maxProfit(int[] prices){
        if (prices == null || prices.length <=0){
            return 0;
        }
        this.prices = prices;
        return iter(0, false, false, 0);
    }
}

 

记忆化搜索：

public class Solution {
    int[] prices;
    Integer[][][] dp;
    int len;

    public int iter(int idx, int have, int frozen, int profit){
        if (dp[idx][have][frozen] != null){
            return dp[idx][have][frozen];
        }

        if (idx == prices.length - 1){
            if (have == 1){
                profit += prices[prices.length - 1];
            }

            dp[idx][have][frozen] = profit;
            return profit;
        }


        int res;
        if (frozen == 1){
            res = iter(idx + 1, 0, 0, profit);
            dp[idx][have][frozen] = res;
            return res;
        }

        if (have == 1){
            int sell = iter(idx+1, 0, 1, profit + prices[idx]);
            int notsell = iter(idx+1, 1, 0, profit);
            res = Math.max(sell, notsell);
            
        }else {
            int buy = iter(idx+1, 1, 0, profit - prices[idx]);
            int notbuy = iter(idx+1, 0, 0, profit);
            res = Math.max(buy, notbuy);
        }
        dp[idx][have][frozen] = res;
        return res;
    }

    public int maxProfit(int[] prices){
        if (prices == null || prices.length <=0){
            return 0;
        }
        this.prices = prices;
        this.len = prices.length;
        dp = new Integer[len][2][2];
        return iter(0, 0, 0, 0);
    }
}

 

dp：

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length <=0){
            return 0;
        }
        int len = prices.length;
        // 这天开始的时候 idx, 有无股票， 是否在冷冻期
        Integer[][][] dp = new Integer[len][2][2];

        dp[len-1][0][0] = 0;
        dp[len-1][1][0] = prices[len-1];
        dp[len-1][0][1] = 0;

        // 不可能出现dp[i][1][1]

        for (int i = len - 2; i >= 0; --i) {
            for (int j = 0; j < 2; j++) {
                for (int k = 0; k < 2; k++) {
                    if (k == 1){
                        if (j != 1){
                            // i 0 1
                            dp[i][j][k] = dp[i+1][0][0];
                        }
                    }
                    else {
                        if (j == 1){
                            // sell / not sell
                            dp[i][j][k] = Math.max(dp[i+1][0][1] + prices[i], dp[i+1][1][0]);
                        }else {
                            // buy / not buy
                            dp[i][j][k] = Math.max(dp[i+1][1][0] - prices[i], dp[i+1][0][0]);
                        }
                    }
                }
            }
        }

        return dp[0][0][0];
    }
}