动态规划dp学习笔记

一、动态规划原理

转自

https://blog.csdn.net/ggdhs/article/details/90641251

https://blog.csdn.net/qq_20011607/article/details/82929611

1. 基本概念

动态规划通过拆分问题，将问题拆分成许多的子问题，定义问题状态和状态之间的关系（即状态转移方程或递推公式），使得问题能够以递推（或者说分治）的方式去解决。按顺序求解子问题，前一子问题的解，为后一子问题的求解提供了有用的信息，在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。 [2] 。

重点在于如何将问题拆分成子问题

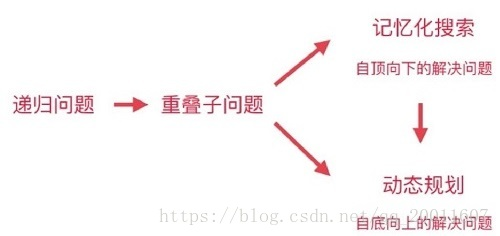
1.1 动态规划和递归之间的关系

动态规划本质上就是递归（+记忆化搜索），动态规划通过将问题划分为若干个子问题，通过递推关系，一步一步求得最终问题的关系。但是子问题之间可能会有重复，因此如果单纯的使用递归方法来实现动态规划问题时间复杂度会比较高。但是，一般能用递归解决的问题都可以转化为用动态规划解决。

2. 动态规划适用情况

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。最优子结构应可以理解为大问题可以不断的分解为小问题，通过每个小问题的最优解可以得到相应大问题的最优解。
（2）无后效性：即某阶段状态（最优解）一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。就比如前面的裴波那契数列的递归算法，进行一次递归f（1）就被计算一次，因此裴波那契数列可以利用动态规划的方法进行求解。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势，在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。）

二、动态规划的经典模型

转自

http://cppblog.com/menjitianya/archive/2015/10/23/212084.html

1、线性模型

线性模型的是动态规划中最常用的模型，上文讲到的最长单调子序列就是经典的线性模型，这里的线性指的是状态的排布是呈线性的。【例题6】是一个经典的面试题，我们将它作为线性模型的敲门砖。

【例题6】在一个夜黑风高的晚上，有n（n <= 50）个小朋友在桥的这边，现在他们需要过桥，但是由于桥很窄，每次只允许不大于两人通过，他们只有一个手电筒，所以每次过桥的两个人需要把手电筒带回来，i号小朋友过桥的时间为T[i]，两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

转自 https://www.cnblogs.com/itlqs/p/5018080.html

首先，下面几句话是显然的：

1.每个人都需要过桥；

2.最慢的两个人过桥后永远不会回来；（因为不会有人需要他们帮着过桥，也不会需要他们送手电筒，当然默认N>=4以保证最慢和最快不重合）

3.最慢的两个人不能在对面没有人而这边还有人的情况下两个人一起过桥；（否则就违反了第二条，必须有一个人回来送手电筒）

好，有了上面三句话，我们很容易得到两个推论。

1.要考虑把N个人送过去的最优时间，只需要先考虑怎么把最慢的两个人先送过去的最优时间。（类似于动态规划中的无后效性）；

2.既然最慢的两个人不能独自过桥，那必须需要别人的帮助。那么需要谁的帮助呢？显然是最快的人的帮助。最快的几个人呢？讨论呗。（但是可以证明最多不超过两个人，因为假设有第三个人，任何一步他的帮助都没有什么作用）

这样，我们就已经知道为什么要选出这四个人了。现在来分析最优方案。

假设，t[1]~t[N] 是从小到大排好序的。设 A=t[1],B=t[2],C=t[N-1],D=t[N].

现在开始讨论：

1.如果C,D需要一个人的帮助过桥。那么最好的方案肯定是A把C送过去，A回来，A把D送过去，A回来。（A必须要回来，因为这边至少还有个B吧~）

T1=C+A+D+A

2.如果C,D需要两个人的帮助过桥。那么最好的方案肯定是A把B送过去，A回来，C和D过去，B回来。（B必须要回来，因为这边至少还有个A吧~）

T2=B+A+D+B

所以，只需要比较T1和T2的大小就可以确定选择哪一个方案。由公式，显然只需要比较A+C和2*B的大小。

而且，这两个方案的初始状态和终止状态都是一样的，而且选择之后的效果都是，左边的人少了两个。

那么问题就自然的转化为了N-2个人的过桥问题。就是递归的思想。

下面分析一下边界。

如果有三个人A,B,C（由小到大）。显然是用A送C，A回来，A送B。时间T=A+B+C。

如果有两个人。时间就是最大的时间。

一个人。时间就是这个人的时间。

2、区间模型

区间模型的状态表示一般为d[i][j]，表示区间[i, j]上的最优解，然后通过状态转移计算出[i+1, j]或者[i, j+1]上的最优解，逐步扩大区间的范围，最终求得[1, len]的最优解。

【例题7】给定一个长度为n（n <= 1000）的字符串A，求插入最少多少个字符使得它变成一个回文串。

典型的区间模型，回文串拥有很明显的子结构特征，即当字符串X是一个回文串时，在X两边各添加一个字符'a'后，aXa仍然是一个回文串，我们用d[i][j]来表示A[i...j]这个子串变成回文串所需要添加的最少的字符数，那么对于A[i] == A[j]的情况，很明显有 d[i][j] = d[i+1][j-1] （这里需要明确一点，当i+1 > j-1时也是有意义的，它代表的是空串，空串也是一个回文串，所以这种情况下d[i+1][j-1] = 0）；当A[i] != A[j]时，我们将它变成更小的子问题求解，我们有两种决策：

1、在A[j]后面添加一个字符A[i]；

2、在A[i]前面添加一个字符A[j]；

根据两种决策列出状态转移方程为：

d[i][j] = min{ d[i+1][j], d[i][j-1] } + 1; (每次状态转移，区间长度增加1)

空间复杂度O(n^2)，时间复杂度O(n^2)，下文会提到将空间复杂度降为O(n)的优化算法。

3、背包模型

背包问题是动态规划中一个最典型的问题之一。由于网上有非常详尽的背包讲解，这里只将常用部分抽出来，具体推导过程详见《背包九讲》。

a.0/1背包

有N种物品（每种物品1件）和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。

决策为第i个物品在前i-1个物品放置完毕后，是选择放还是不放，状态转移方程为：

f[i][v] = max{ f[i-1][v], f[i-1][v - Ci] +Wi }

时间复杂度O(VN)，空间复杂度O(VN) （空间复杂度可利用滚动数组进行优化达到O(V)，下文会介绍滚动数组优化）。

b.完全背包

有N种物品（每种物品无限件）和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

https://www.cnblogs.com/mfrank/p/10803417.html

c.多重背包

https://www.cnblogs.com/mfrank/p/10816837.html

【例题8】一群强盗想要抢劫银行，总共N(N <= 100)个银行，第i个银行的资金为Bi亿，抢劫该银行被抓概率Pi，问在被抓概率小于p的情况下能够抢劫的最大资金是多少？

p表示的是强盗在抢银行时至少有一次被抓概率的上限，那么选择一些银行，并且计算抢劫这些银行都不被抓的的概率pc，则需要满足1 - pc < p。这里的pc是所有选出来的银行的抢劫时不被抓概率（即1 - Pi）的乘积，于是我们用资金作为背包物品的容量，概率作为背包物品的价值，求01背包。状态转移方程为：