【bzoj3774】最优选择 网络流最小割

题目描述 

小N手上有一个N*M的方格图，控制某一个点要付出Aij的代价，然后某个点如果被控制了，或者他周围的所有点(上下左右)都被控制了，那么他就算是被选择了的。一个点如果被选择了，那么可以得到Bij的回报，现在请你帮小N选一个最优的方案，使得回报-代价尽可能大。

输入

第一行两个正整数N,M表示方格图的长与宽。

接下来N行每行M个整数Aij表示控制的代价。

接下来N行每行M个整数Bij表示选择的回报。

输出

一个整数，表示最大的回报-代价(如果一个都不控制那么就是0)。

样例输入

3 3
1 100 100
100 1 100
1 100 100
2 0 0
5 2 0
2 0 0

样例输出

8

---

题解

网络流最小割

先求出所有价值的总和，然后对于每个点：要么付出选择代价，要么放弃价值，要么相邻点付出选择代价。

考虑构建a-b-inf-a'的结构。

每个点拆成两个（以下称1和2），中间连容量为b的边，表示价值。将原图黑白染色，对于黑点：S向1连边，容量为a；对于白点：2向T连边，容量为a，表示付出选择代价。

对于黑点：该点的2向相邻点（显然是白点）的2连边，容量为inf，这样就有了a-b-inf-a'的结构；对于白点：相邻点的1向该点的1连边，容量为inf，这样就有了a'-inf-b-a的结构。

建出来的图大概长这样（B为黑点，W为白点）：

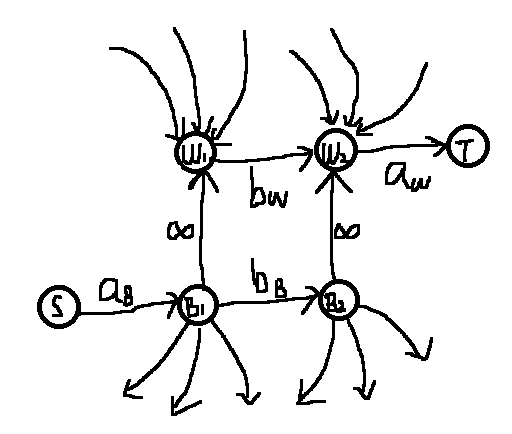
总收益减去最小割即为答案。

#include <queue>
#include <cstdio>
#include <cstring>
#define N 5010
#define M 100010
#define inf 1 << 30
#define pos(h , i , j) ((h - 1) * n * m + (i - 1) * m + j)
using namespace std;
queue<int> q;
int head[N] , to[M] , val[M] , next[M] , cnt = 1 , s , t , dis[N];
inline void add(int x , int y , int z)
{
	to[++cnt] = y , val[cnt] = z , next[cnt] = head[x] , head[x] = cnt;
	to[++cnt] = x , val[cnt] = 0 , next[cnt] = head[y] , head[y] = cnt;
}
bool bfs()
{
	int x , i;
	memset(dis , 0 , sizeof(dis));
	while(!q.empty()) q.pop();
	dis[s] = 1 , q.push(s);
	while(!q.empty())
	{
		x = q.front() , q.pop();
		for(i = head[x] ; i ; i = next[i])
		{
			if(val[i] && !dis[to[i]])
			{
				dis[to[i]] = dis[x] + 1;
				if(to[i] == t) return 1;
				q.push(to[i]);
			}
		}
	}
	return 0;
}
int dinic(int x , int low)
{
	if(x == t) return low;
	int temp = low , i , k;
	for(i = head[x] ; i ; i = next[i])
	{
		if(val[i] && dis[to[i]] == dis[x] + 1)
		{
			k = dinic(to[i] , min(temp , val[i]));
			if(!k) dis[to[i]] = 0;
			val[i] -= k , val[i ^ 1] += k;
			if(!(temp -= k)) break;
		}
	}
	return low - temp;
}
int main()
{
	int n , m , i , j , x , ans = 0;
	scanf("%d%d" , &n , &m) , s = 0 , t = 2 * n * m + 1;
	for(i = 1 ; i <= n ; i ++ )
	{
		for(j = 1 ; j <= m ; j ++ )
		{
			scanf("%d" , &x);
			if((i ^ j) & 1)
			{
				add(s , pos(1 , i , j) , x);
				if(i > 1) add(pos(1 , i , j) , pos(1 , i - 1 , j) , inf) , add(pos(2 , i , j) , pos(2 , i - 1 , j) , inf);
				if(i < n) add(pos(1 , i , j) , pos(1 , i + 1 , j) , inf) , add(pos(2 , i , j) , pos(2 , i + 1 , j) , inf);
				if(j > 1) add(pos(1 , i , j) , pos(1 , i , j - 1) , inf) , add(pos(2 , i , j) , pos(2 , i , j - 1) , inf);
				if(j < m) add(pos(1 , i , j) , pos(1 , i , j + 1) , inf) , add(pos(2 , i , j) , pos(2 , i , j + 1) , inf);
			}
			else add(pos(2 , i , j) , t , x);
		}
	}
	for(i = 1 ; i <= n ; i ++ )
		for(j = 1 ; j <= m ; j ++ )
			scanf("%d" , &x) , add(pos(1 , i , j) , pos(2 , i , j) , x) , ans += x;
	while(bfs()) ans -= dinic(s , inf);
	printf("%d\n" , ans);
	return 0;
}