【bzoj2438】[中山市选2011]杀人游戏 Tarjan
题目描述
一位冷血的杀手潜入 Na-wiat,并假装成平民。警察希望能在 N 个人里面,查出谁是杀手。警察能够对每一个人进行查证,假如查证的对象是平民,他会告诉警察,他认识的人, 谁是杀手, 谁是平民。 假如查证的对象是杀手, 杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手,可看作他们是杀手的概率是相同的。问:根据最优的情况,保证警察自身安全并知道谁是杀手的概率最大是多少?
输入
第一行有两个整数 N,M。
接下来有 M 行,每行两个整数 x,y,表示 x 认识 y(y 不一定认识 x) 。
输出
仅包含一行一个实数,保留小数点后面 6 位,表示最大概率。
样例输入
5 4
1 2
1 3
1 4
1 5
样例输出
0.800000
题解
Tarjan
显然只需要查证所有 缩点后入度为0的强连通分量中的任意一个点 即可,即必须查证的人的个数等于入度为0的强连通分量个数。
但是这并不一定是最优解。考虑一种情况:
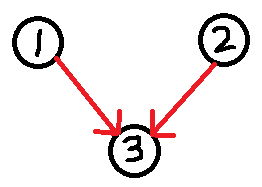
这时只需要查证2(或者查证1)即可,可以不查证1(或2)。
具体原因是:一个入度为0的强连通分量大小为1,如果它指向的所有点都不仅由它到达(即减去它到其的边数后入度不为0),那么可以先查证其它点,直到最后仅剩下这个点,即可不查证该点。
于是需要再统计一下是否有这种情况。具体方法:枚举每个点,判断它所有能够到达的点是否仅由它到达即可。注意这样的点只能保留1个(多了无法排除),因此需要及时终止循环。
最后 (n-必须查证的人)/n 即为存活概率。
时间复杂度$O(n+m)$
#include <cstdio>
#include <algorithm>
#define N 100010
#define M 300010
using namespace std;
int head[N] , to[M] , next[M] , cnt , deep[N] , low[N] , tot , vis[N] , ins[N] , sta[N] , top , bl[N] , si[N] , num , ind[N];
inline void add(int x , int y)
{
to[++cnt] = y , next[cnt] = head[x] , head[x] = cnt;
}
void tarjan(int x)
{
int i;
deep[x] = low[x] = ++tot , vis[x] = ins[x] = 1 , sta[++top] = x;
for(i = head[x] ; i ; i = next[i])
{
if(!vis[to[i]]) tarjan(to[i]) , low[x] = min(low[x] , low[to[i]]);
else if(ins[to[i]]) low[x] = min(low[x] , deep[to[i]]);
}
if(deep[x] == low[x])
{
int t;
num ++ ;
do
{
t = sta[top -- ] , si[num] ++ ;
ins[t] = 0 , bl[t] = num;
}while(t != x);
}
}
bool judge(int x)
{
int i;
bool flag = 1;
for(i = head[x] ; i ; i = next[i]) ind[bl[to[i]]] -- ;
for(i = head[x] ; i ; i = next[i])
if(!ind[bl[to[i]]])
flag = 0;
for(i = head[x] ; i ; i = next[i]) ind[bl[to[i]]] ++ ;
return flag;
}
int main()
{
int n , m , i , x , y , ans = 0;
scanf("%d%d" , &n , &m);
for(i = 1 ; i <= m ; i ++ ) scanf("%d%d" , &x , &y) , add(x , y);
for(i = 1 ; i <= n ; i ++ )
if(!vis[i])
tarjan(i);
for(x = 1 ; x <= n ; x ++ )
for(i = head[x] ; i ; i = next[i])
if(bl[x] != bl[to[i]])
ind[bl[to[i]]] ++ ;
for(i = 1 ; i <= num ; i ++ )
if(!ind[i])
ans ++ ;
for(i = 1 ; i <= n ; i ++ )
if(si[bl[i]] == 1 && !ind[bl[i]] && judge(i))
break;
if(i <= n) ans -- ;
printf("%.6lf\n" , (double)(n - ans) / n);
return 0;
}
