【bzoj1002】[FJOI2007]轮状病毒 矩阵树定理+高精度
题目描述
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的,2个原子之间的边表示这2个原子之间的信息通道。如下图所示
.png)
N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不同的3轮状病毒,如下图所示
.png)
现给定n(N<=100),编程计算有多少个不同的n轮状病毒
输入
第一行有1个正整数n
输出
计算出的不同的n轮状病毒数输出
样例输入
3
样例输出
16
题解
矩阵树定理+高精度
求无向图生成树个数,显然使用矩阵树定理。
然后得到的行列式如下:
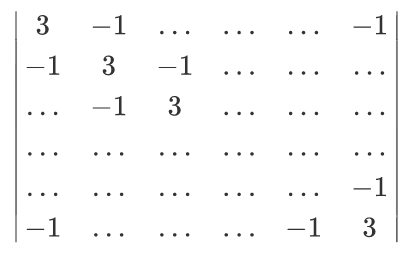
(-1和3处是相同的结构,其余位置为0)
然后可以使用高精度小数进行高斯消元,不过这样显然不够优雅。
手推一下这个行列式的性质,可以发现:$F(n)=3*F(n-1)-F(n-2)+2$。
这样就可以直接递推了。
高精度什么的使用Python就好啦。
n = int(input()) f = [0] * 105 f[1] = 1 for i in range(2 , n + 1): f[i] = 3 * f[i - 1] - f[i - 2] + 2 print(f[n])

