hashc长度拓展攻击
一、hash长度攻击的简要介绍
1、首先什么是hash长度拓展攻击?
简单来说,由于hash的生成机制原因,使得我们可以认为的在原先明文数据的基础上添加新的拓展字符,使得原本的加密链变长,进而控制加密链的最后一节,使得我们得以控制最终结果。
也就是说当我们知道hash(secret+data)的值以及secret的长度的情况下,我们就可以推算出hash(secret+data||padding||a)在这里padding是secret后面的填充内容,包含整个消息的长度,a可以是任何数据,我们需要知道secret的长度,这样才能够计算出padding。
2、什么是hash算法?
哈希算法(Hash算法)是一种将任意长度的消息压缩到固定长度的消息摘要的数学函数。哈希算法将输入消息(也称为明文)作为输入,并生成唯一的固定长度的输出,该输出称为哈希值,摘要或指纹。哈希值通常用于数字签名,数据完整性校验,数据索引和加密等安全应用中。常见的hash算法包括md5,sha-1,sha-256等。
二、MD5算法的加密流程
想要搞清楚hash长度拓展攻击的逻辑,就要先理清楚hash算法的加密流程。
这里以md5加密为例进行分析。
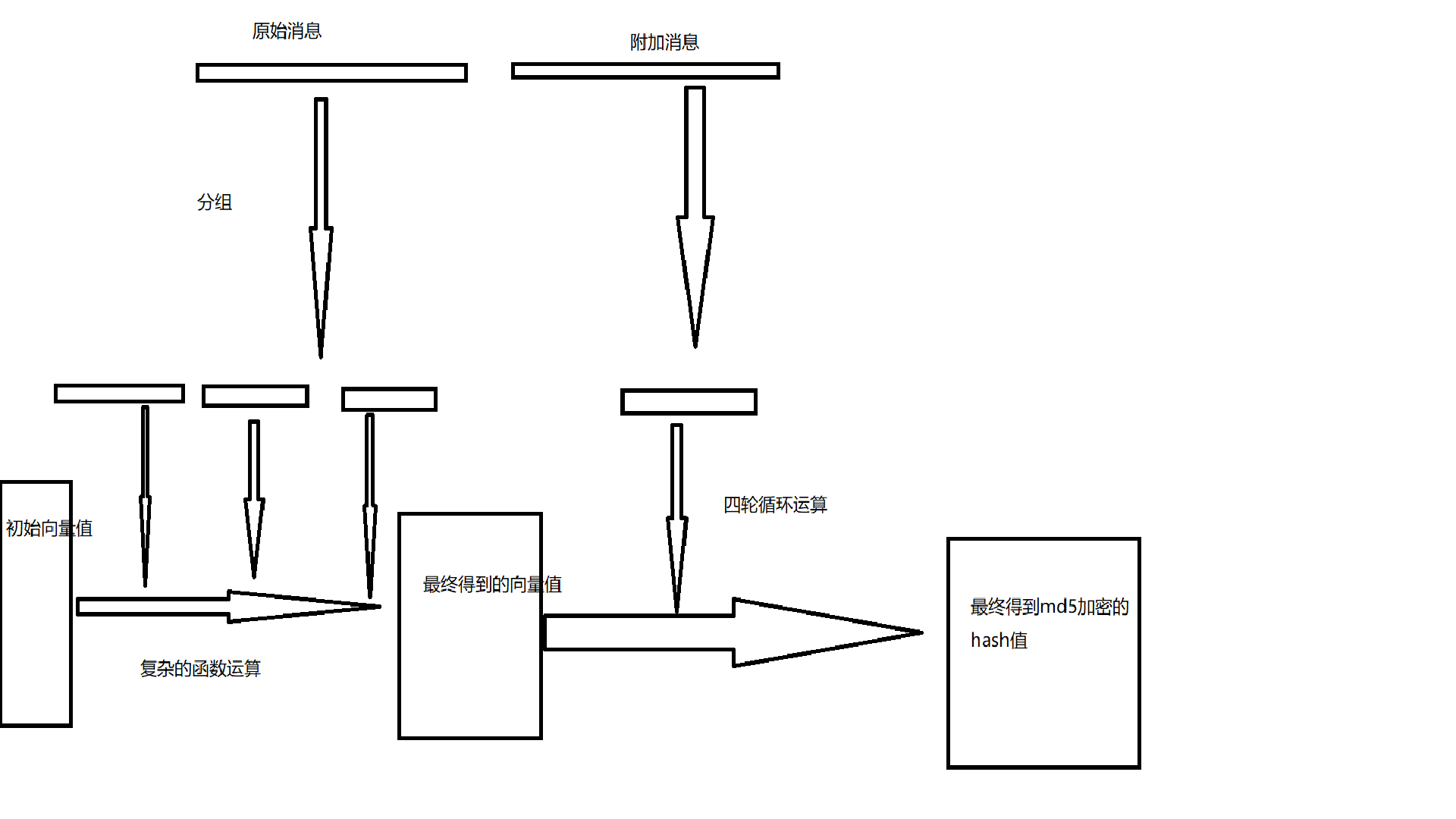
md5的加密流程,大概分为以下几部分:
1、填充消息
2、添加长度信息
3、初始化状态
4、分组处理进行复杂函数处理
5、输出结果
下面我们大概分析一下每个步骤的过程:
1、填充消息
将原始消息(字节序列)填充到长度为448 mod 512的位置,使得填充后的消息长度为512的整数倍。填充方式为在原始消息末尾添加一个1,后面再补0直到长度满足要求。
也就是说当消息长度小于56个字节时要讲其填充到56个字节,大于等于56字节的要填充到对64取余的余数为8个字节.
如下图所示:
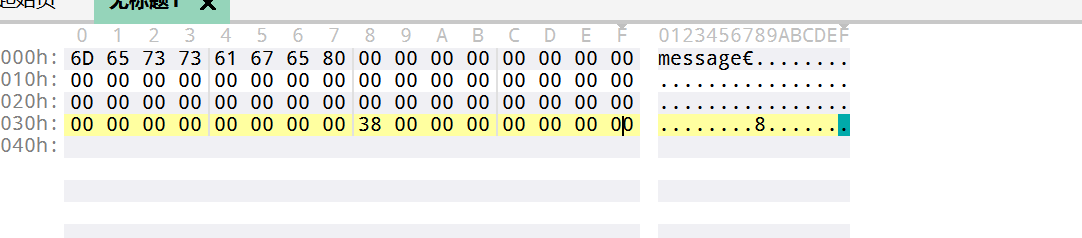
加入我们对,message进行填充:

这里的80是16进制,其代表的是二进制下面的10000000,那么这里就是补一个1和若干0,把消息补位到56个字节,也就是448bit.
2、存储长度信息
上面补位后,上面消息长度以及达到了56字节,从第57字节开始存储补位之前消息的长度
长度是小端存储。也就是高字节存放在高地址
我们还以上面的例为例:
字符串message的长度为7个字母,也就是56byte 换算成16进制是0x38
即:
3、初始化状态
md5使用四个32为寄存器(A,B,C,D)保存中间运算结果,初始值为常量,具体来说,A,B,C,D的初始值如下:
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476
4、分组处理进行复杂函数处理
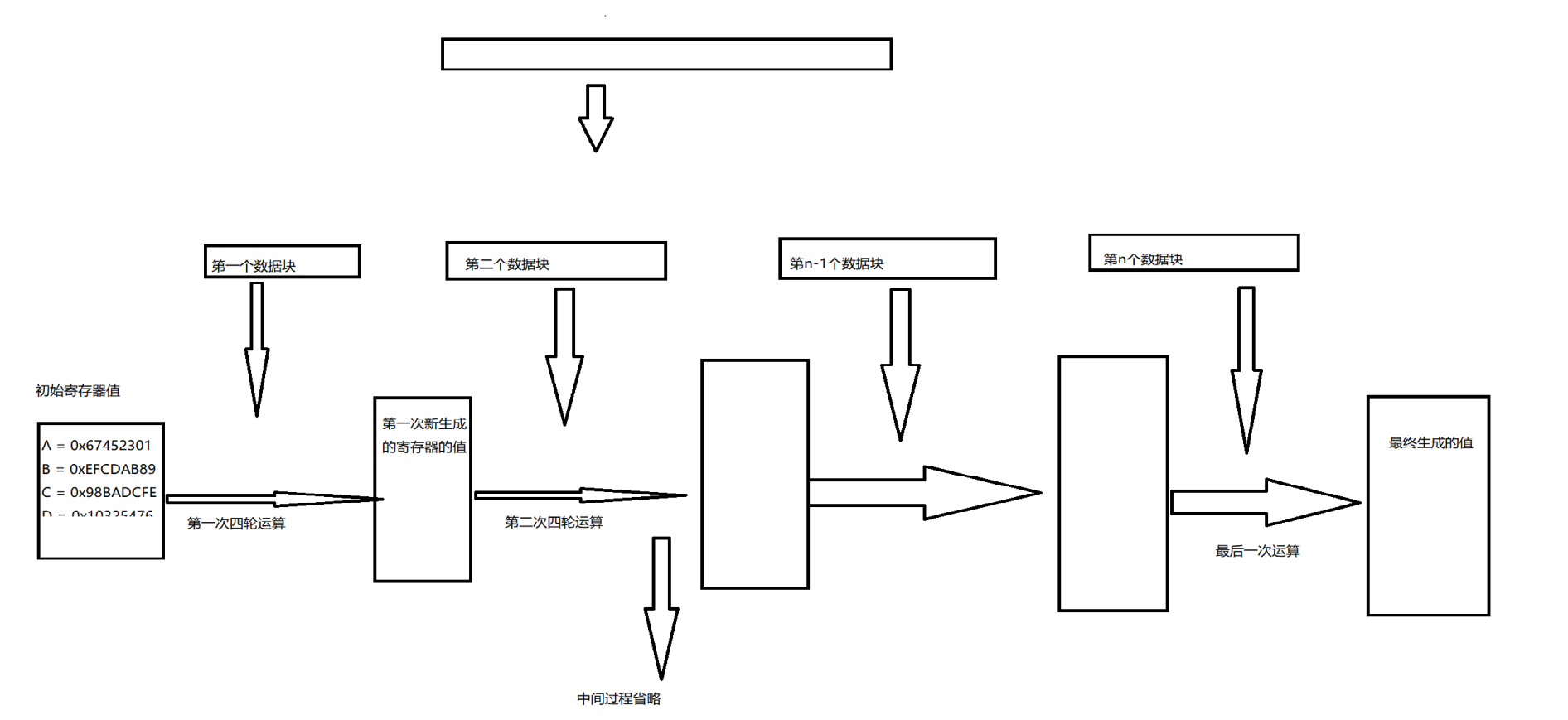
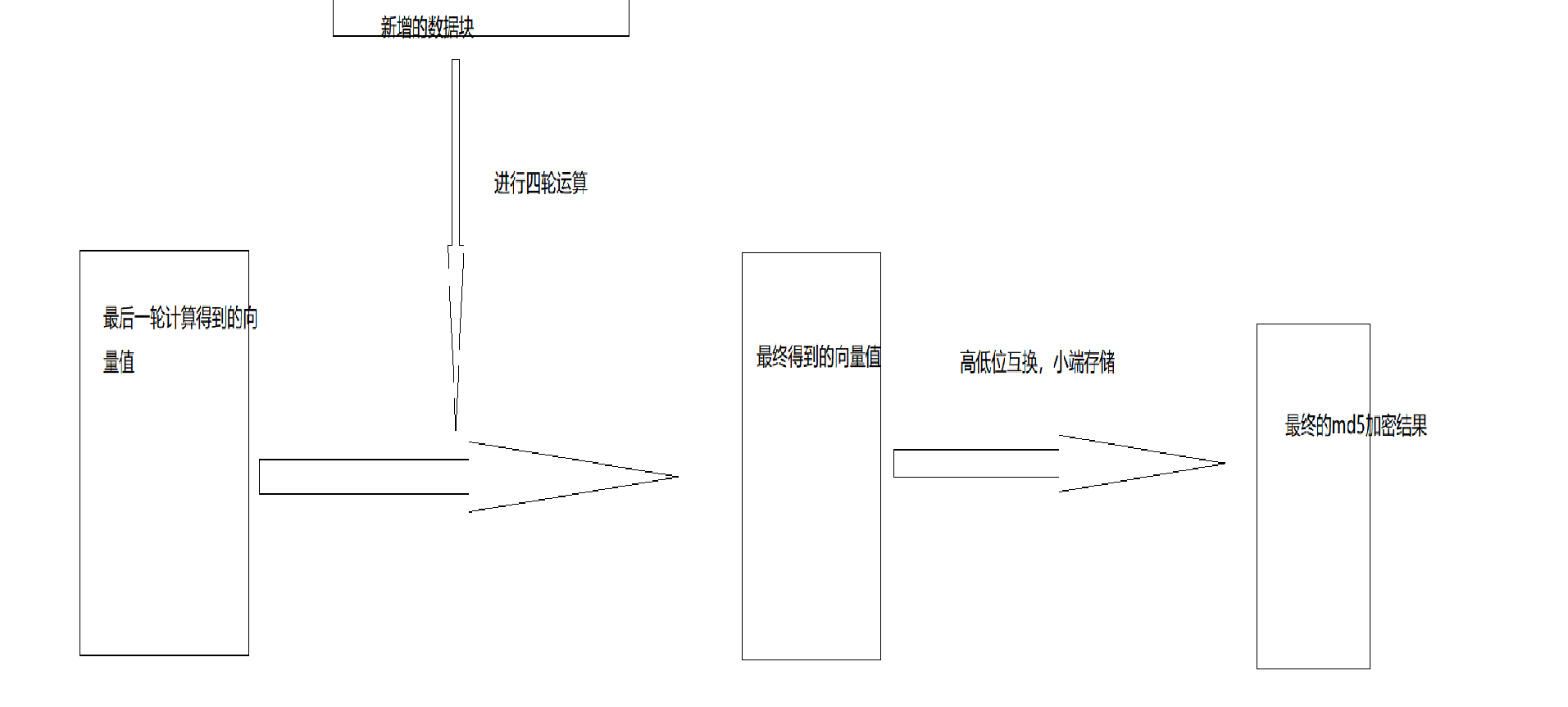
将填充后的消息分为若干个512位的消息块。对于每个消息块,MD5算法执行四轮循环,每轮循环包含16次操作,共计64次操作。每次操作都使用一个消息块中的32位字作为输入,对寄存器A、B、C、D进行修改,最终输出新的A、B、C、D的值。
也就是说第一个数据块与初始向量进行四轮循环,生成第一个新的字符串,保存在寄存器A,B,C,D中,寄存器继续与第二个数据块进行运算,直到最后一个数据块。
其过程可以理解为:
5、结果的输出
假设最终生成的寄存器的值是:
A=0xab45bc01
B=0x6a64bb53
C=0x23ba8afe
D=0x46847a62
先两两一组进行组合,得到下面的数据
ab 45 bc 01
6a 64 bb 53
23 ba 8a fe
46 84 7a 62
在进行高低位互换:
01 bc 45 ab
53 bb 64 6a
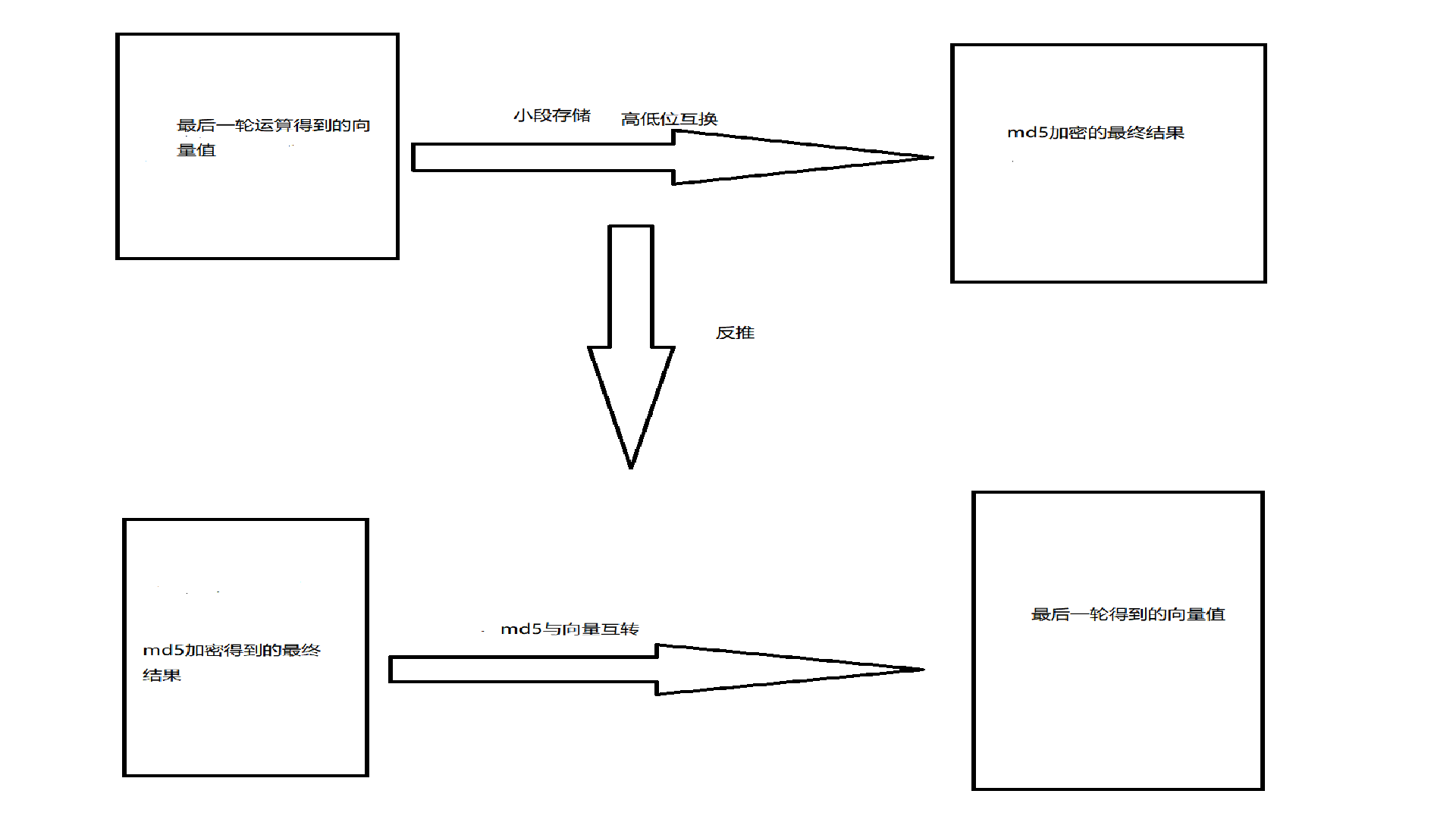
最终拼接在一起就能够得到md5的值
这就是md5加密的大概过程
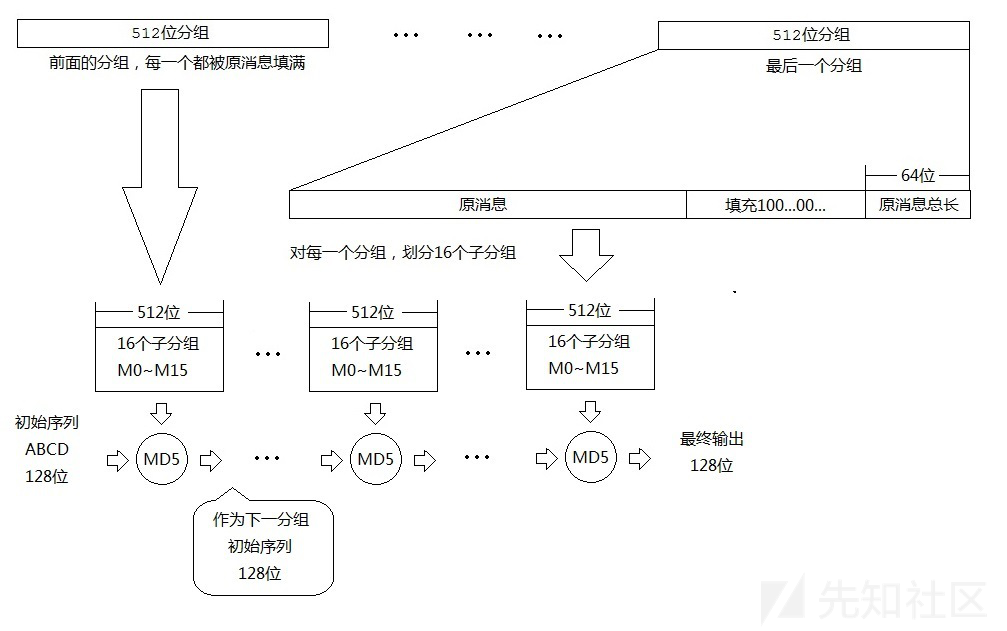
下面这是网上找来的流程图:
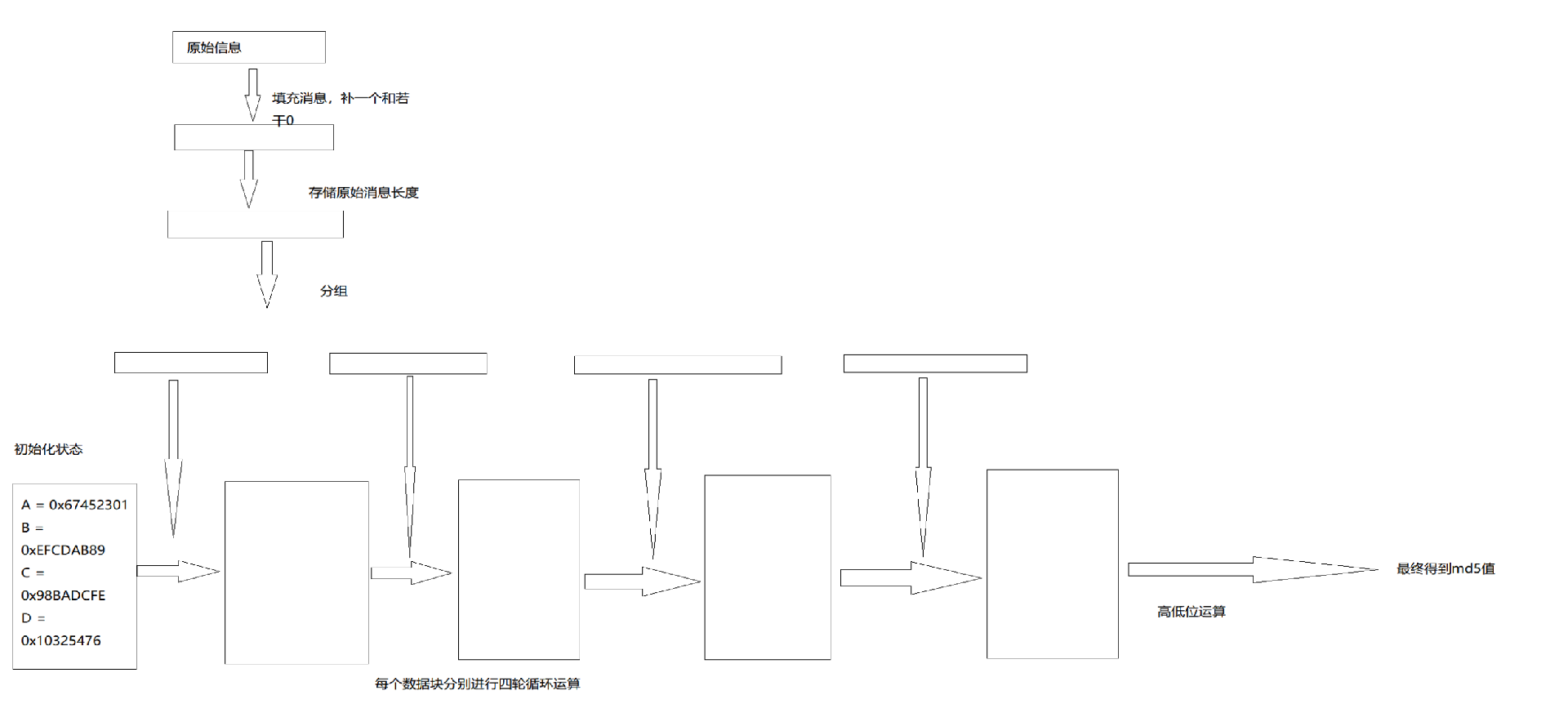
下面是我按自己的理解搞得一个流程图:
三、hash长度拓展攻击逻辑分析
上面我们对md5的加密流程进行了大概的分析
下面我们通过md5的加密流程对hash长度拓展攻击逻辑进行分析
我们这里通过一道题目进行分析:
这是22年12月举办的铁三信息安全比赛的一道原题:
代码:
<?php
error_reporting(0);
include "flag.php";
$user = $_POST['user'];
function encrypt($text)
{
global $key;
return md5($key . $text);
}
if (encrypt($user) === $_COOKIE['verify']) {
if (is_numeric(strpos($user, 'root'))) {
die($flag);
} else {
die('not root!!!');
}
} else {
setcookie("verify", encrypt("guest"), time() + 60 * 60 * 24);
setcookie("len", strlen($key), time() + 60 * 60 * 24);
}
highlight_file(__FILE__);
?>
这里可以看到
获得flag的条件:
if (encrypt($user) === $_COOKIE['verify']) {
if (is_numeric(strpos($user, 'root'))) {
我们输入的user经过md5加密后要与cookie里面的vefify相等,并且在输入的user里面要有root
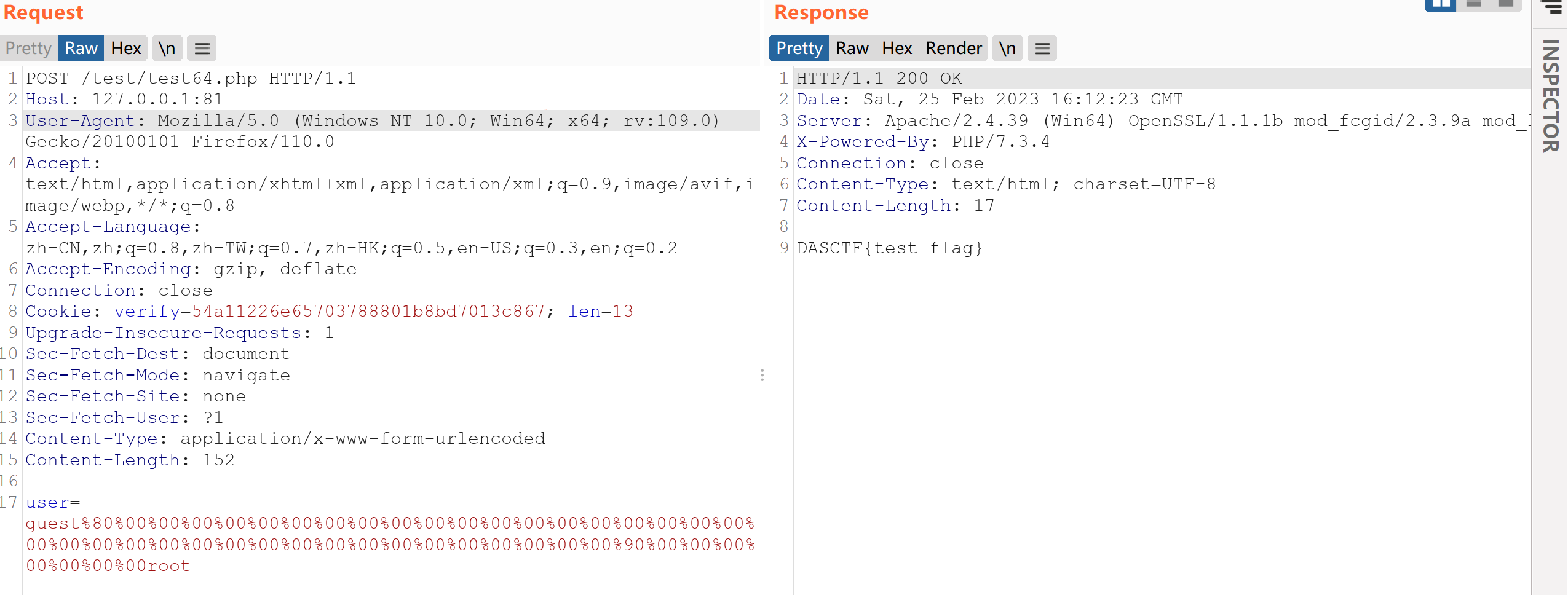
看一下响应包:
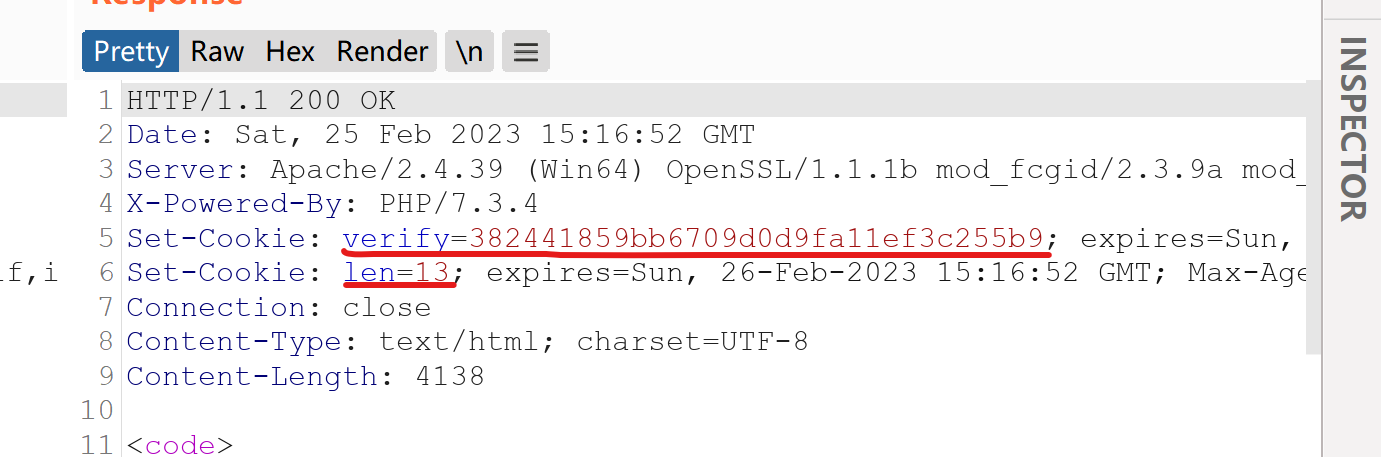
可以得到hash(secert+guest)的值为382441859bb6709d0d9fa11ef3c255b9,secert的长度为13
那我们这里重复一下md5加密的流程:
首先是数据填充:(这里假设secret是13个A)

然后进行原始消息数据填充
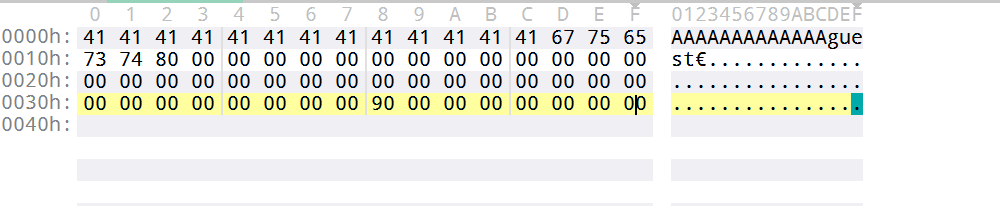
18个字符,144byte 转换为16进制表示为0x90
后面就是将填充后的消息分成若干个512位的位块,然后与初始向量进行四轮循环运算,这里不再详细讲,
直到最后一个数据块与寄存器中的向量值进行四轮损害运算,得到最终向量值(A',B',C',D'),在经过高低位运算就可以得到最终的md5加密的hash值。
那么我们回到题目,通过响应包我们可以得到hash(secret+guest)的值382441859bb6709d0d9fa11ef3c255b9
那我们可以推出最后得到向量值为:
A'=0x85412438
B'=0x9d70b69b
C'=0x1ea19f0d
D'=0xb955c2f3
题目要求要匹配到root,但是我们并不知道secret,所以这里可以使用hash长度拓展攻击
首先我们把要添加的数据添加上去
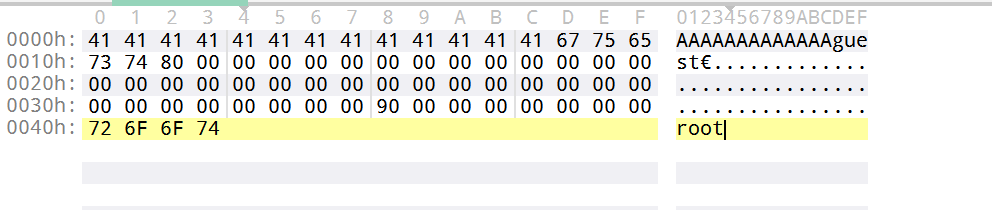
根据md5填充规则进行填充:
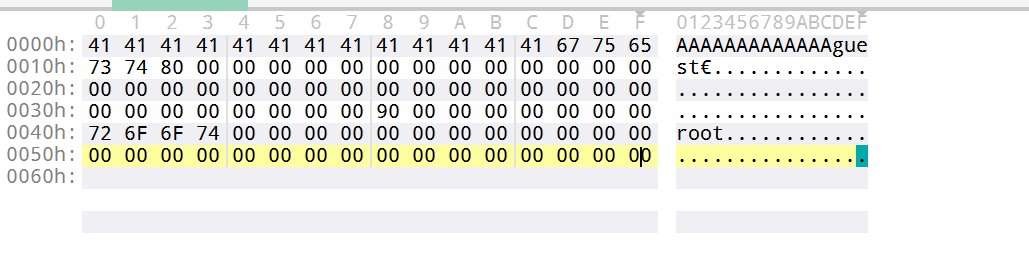
去掉前面的我们假设的secret给去除掉,可以得到
guest\0x80\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00\0x00....\0x00\0x00\0x00\0x00\0x00\0x00\0x90\0x00\0x00\0x00\0x00\0x00\0x00\0x00root
进行url编码:
guest%00x80%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00..x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x00%00x90%00x00%00x00%00x00%00x00%00x00%00x00%00x00root
这里我们虽然通过添加的方法使得字符串中有了root,但是由于我们并不知道secret,导致我们并没有办法计算出md5加密后hash值。但是由于我们实在hash(secret+guest)的hash值,但是我们这里填加了数据,所以导致还要再进行一轮运算,那么我们就可以再不知道secret的情况下计算出正确的md5加密的hash值。
这里我们上面计算出了最后一轮加密的向量值为:
A'=0x85412438
B'=0x9d70b69b
C'=0x1ea19f0d
D'=0xb955c2f3
由于我们添加了新的字符串,导致分组时分的数据块会增加,那么hash(secret+guest)的值并不是我们最终要得到的md5值,而是做完向量串继续与后面新增加的数据块进行运算,那么这样的话我们就可以再不知道secret的情况下获得md5加密的hash值。
但是这个计算式非常复杂的,我们这里使用找到的脚本进行计算:
my_md5.py:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author:DshtAnger
# theory reference:
# blog:
# http://blog.csdn.net/adidala/article/details/28677393
# http://blog.csdn.net/forgotaboutgirl/article/details/7258109
# http://blog.sina.com.cn/s/blog_6fe0eb1901014cpl.html
# RFC1321:
# https://www.rfc-editor.org/rfc/pdfrfc/rfc1321.txt.pdf
##############################################################################
import sys
def genMsgLengthDescriptor(msg_bitsLenth):
'''
---args:
msg_bitsLenth : the bits length of raw message
--return:
16 hex-encoded string , i.e.64bits,8bytes which used to describe the bits length of raw message added after padding
'''
return __import__("struct").pack(">Q",msg_bitsLenth).encode("hex")
def reverse_hex_8bytes(hex_str):
'''
--args:
hex_str: a hex-encoded string with length 16 , i.e.8bytes
--return:
transform raw message descriptor to little-endian
'''
hex_str = "%016x"%int(hex_str,16)
assert len(hex_str)==16
return __import__("struct").pack("<Q",int(hex_str,16)).encode("hex")
def reverse_hex_4bytes(hex_str):
'''
--args:
hex_str: a hex-encoded string with length 8 , i.e.4bytes
--return:
transform 4 bytes message block to little-endian
'''
hex_str = "%08x"%int(hex_str,16)
assert len(hex_str)==8
return __import__("struct").pack("<L",int(hex_str,16)).encode("hex")
def deal_rawInputMsg(input_msg):
'''
--args:
input_msg : inputed a ascii-encoded string
--return:
a hex-encoded string which can be inputed to mathematical transformation function.
'''
ascii_list = [x.encode("hex") for x in input_msg]
length_msg_bytes = len(ascii_list)
length_msg_bits = len(ascii_list)*8
#padding
ascii_list.append('80')
while (len(ascii_list)*8+64)%512 != 0:
ascii_list.append('00')
#add Descriptor
ascii_list.append(reverse_hex_8bytes(genMsgLengthDescriptor(length_msg_bits)))
return "".join(ascii_list)
def getM16(hex_str,operatingBlockNum):
'''
--args:
hex_str : a hex-encoded string with length in integral multiple of 512bits
operatingBlockNum : message block number which is being operated , greater than 1
--return:
M : result of splited 64bytes into 4*16 message blocks with little-endian
'''
M = [int(reverse_hex_4bytes(hex_str[i:(i+8)]),16) for i in xrange(128*(operatingBlockNum-1),128*operatingBlockNum,8)]
return M
#定义函数,用来产生常数T[i],常数有可能超过32位,同样需要&0xffffffff操作。注意返回的是十进制的数
def T(i):
result = (int(4294967296*abs(__import__("math").sin(i))))&0xffffffff
return result
#定义每轮中用到的函数
#RL为循环左移,注意左移之后可能会超过32位,所以要和0xffffffff做与运算,确保结果为32位
F = lambda x,y,z:((x&y)|((~x)&z))
G = lambda x,y,z:((x&z)|(y&(~z)))
H = lambda x,y,z:(x^y^z)
I = lambda x,y,z:(y^(x|(~z)))
RL = L = lambda x,n:(((x<<n)|(x>>(32-n)))&(0xffffffff))
def FF(a, b, c, d, x, s, ac):
a = (a+F ((b), (c), (d)) + (x) + (ac)&0xffffffff)&0xffffffff;
a = RL ((a), (s))&0xffffffff;
a = (a+b)&0xffffffff
return a
def GG(a, b, c, d, x, s, ac):
a = (a+G ((b), (c), (d)) + (x) + (ac)&0xffffffff)&0xffffffff;
a = RL ((a), (s))&0xffffffff;
a = (a+b)&0xffffffff
return a
def HH(a, b, c, d, x, s, ac):
a = (a+H ((b), (c), (d)) + (x) + (ac)&0xffffffff)&0xffffffff;
a = RL ((a), (s))&0xffffffff;
a = (a+b)&0xffffffff
return a
def II(a, b, c, d, x, s, ac):
a = (a+I ((b), (c), (d)) + (x) + (ac)&0xffffffff)&0xffffffff;
a = RL ((a), (s))&0xffffffff;
a = (a+b)&0xffffffff
return a
def show_md5(A,B,C,D):
return "".join( [ "".join(__import__("re").findall(r"..","%08x"%i)[::-1]) for i in (A,B,C,D) ] )
def run_md5(A=0x67452301,B=0xefcdab89,C=0x98badcfe,D=0x10325476,readyMsg=""):
a = A
b = B
c = C
d = D
for i in xrange(0,len(readyMsg)/128):
M = getM16(readyMsg,i+1)
for i in xrange(16):
exec "M"+str(i)+"=M["+str(i)+"]"
#First round
a=FF(a,b,c,d,M0,7,0xd76aa478L)
d=FF(d,a,b,c,M1,12,0xe8c7b756L)
c=FF(c,d,a,b,M2,17,0x242070dbL)
b=FF(b,c,d,a,M3,22,0xc1bdceeeL)
a=FF(a,b,c,d,M4,7,0xf57c0fafL)
d=FF(d,a,b,c,M5,12,0x4787c62aL)
c=FF(c,d,a,b,M6,17,0xa8304613L)
b=FF(b,c,d,a,M7,22,0xfd469501L)
a=FF(a,b,c,d,M8,7,0x698098d8L)
d=FF(d,a,b,c,M9,12,0x8b44f7afL)
c=FF(c,d,a,b,M10,17,0xffff5bb1L)
b=FF(b,c,d,a,M11,22,0x895cd7beL)
a=FF(a,b,c,d,M12,7,0x6b901122L)
d=FF(d,a,b,c,M13,12,0xfd987193L)
c=FF(c,d,a,b,M14,17,0xa679438eL)
b=FF(b,c,d,a,M15,22,0x49b40821L)
#Second round
a=GG(a,b,c,d,M1,5,0xf61e2562L)
d=GG(d,a,b,c,M6,9,0xc040b340L)
c=GG(c,d,a,b,M11,14,0x265e5a51L)
b=GG(b,c,d,a,M0,20,0xe9b6c7aaL)
a=GG(a,b,c,d,M5,5,0xd62f105dL)
d=GG(d,a,b,c,M10,9,0x02441453L)
c=GG(c,d,a,b,M15,14,0xd8a1e681L)
b=GG(b,c,d,a,M4,20,0xe7d3fbc8L)
a=GG(a,b,c,d,M9,5,0x21e1cde6L)
d=GG(d,a,b,c,M14,9,0xc33707d6L)
c=GG(c,d,a,b,M3,14,0xf4d50d87L)
b=GG(b,c,d,a,M8,20,0x455a14edL)
a=GG(a,b,c,d,M13,5,0xa9e3e905L)
d=GG(d,a,b,c,M2,9,0xfcefa3f8L)
c=GG(c,d,a,b,M7,14,0x676f02d9L)
b=GG(b,c,d,a,M12,20,0x8d2a4c8aL)
#Third round
a=HH(a,b,c,d,M5,4,0xfffa3942L)
d=HH(d,a,b,c,M8,11,0x8771f681L)
c=HH(c,d,a,b,M11,16,0x6d9d6122L)
b=HH(b,c,d,a,M14,23,0xfde5380c)
a=HH(a,b,c,d,M1,4,0xa4beea44L)
d=HH(d,a,b,c,M4,11,0x4bdecfa9L)
c=HH(c,d,a,b,M7,16,0xf6bb4b60L)
b=HH(b,c,d,a,M10,23,0xbebfbc70L)
a=HH(a,b,c,d,M13,4,0x289b7ec6L)
d=HH(d,a,b,c,M0,11,0xeaa127faL)
c=HH(c,d,a,b,M3,16,0xd4ef3085L)
b=HH(b,c,d,a,M6,23,0x04881d05L)
a=HH(a,b,c,d,M9,4,0xd9d4d039L)
d=HH(d,a,b,c,M12,11,0xe6db99e5L)
c=HH(c,d,a,b,M15,16,0x1fa27cf8L)
b=HH(b,c,d,a,M2,23,0xc4ac5665L)
#Fourth round
a=II(a,b,c,d,M0,6,0xf4292244L)
d=II(d,a,b,c,M7,10,0x432aff97L)
c=II(c,d,a,b,M14,15,0xab9423a7L)
b=II(b,c,d,a,M5,21,0xfc93a039L)
a=II(a,b,c,d,M12,6,0x655b59c3L)
d=II(d,a,b,c,M3,10,0x8f0ccc92L)
c=II(c,d,a,b,M10,15,0xffeff47dL)
b=II(b,c,d,a,M1,21,0x85845dd1L)
a=II(a,b,c,d,M8,6,0x6fa87e4fL)
d=II(d,a,b,c,M15,10,0xfe2ce6e0L)
c=II(c,d,a,b,M6,15,0xa3014314L)
b=II(b,c,d,a,M13,21,0x4e0811a1L)
a=II(a,b,c,d,M4,6,0xf7537e82L)
d=II(d,a,b,c,M11,10,0xbd3af235L)
c=II(c,d,a,b,M2,15,0x2ad7d2bbL)
b=II(b,c,d,a,M9,21,0xeb86d391L)
A += a
B += b
C += c
D += d
A = A&0xffffffff
B = B&0xffffffff
C = C&0xffffffff
D = D&0xffffffff
a = A
b = B
c = C
d = D
return show_md5(a,b,c,d)
exp.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import my_md5
samplehash="382441859bb6709d0d9fa11ef3c255b9"
#将哈希值分为四段,并反转该四字节为小端序,作为64第二次循环的输入幻书
s1=0x85412438
s2=0x9d70b69b
s3=0x1ea19f0d
s4=0xb955c2f3
#exp
secret = "A"*13
secret_admin = secret + 'guest{padding}'
padding = '\x80{zero}\xc8\x00\x00\x00\x00\x00\x00\x00'.format(zero="\x00"*(64-15-10-1-8))
secret_admin = secret_admin.format(padding=padding) + 'root'
r = my_md5.deal_rawInputMsg(secret_admin)
inp = r[len(r)/2:] #我们需要截断的地方,也是我们需要控制的地方
print "getmein:"+my_md5.run_md5(s1,s2,s3,s4,inp)
这里使用脚本没有计算出来,可能是自己哪里的配置有错误,但是脚本不知道怎么改,就只能使用其他师傅写好的工具去运算。
流程图:
四、hashpump工具的安装与使用
git clone https://github.com/bwall/HashPump
apt-get install g++ libssl-dev
cd HashPump
make
make install
使用方法:

那么我们回到题目进行验证:
进行url编码:
guest%80%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%00%90%00%00%00%00%00%00%00root
可以看到以及攻击成功了。
五、防御方法
以下是一些防御哈希长度拓展攻击的方法:
1、使用加盐(Salting)技术
加盐技术是将一个随机字符串添加到原始数据之后,再进行哈希计算。由于加盐字符串是随机的,攻击者无法通过已知的哈希值推算出加盐字符串的内容,从而无法利用哈希长度拓展攻击。加盐技术是防御哈希长度拓展攻击的常见方法。
2、使用不可逆加密算法
不可逆加密算法将原始数据转换为不可逆的密文,防止攻击者通过逆向计算推算出原始数据。相比哈希算法,不可逆加密算法的计算复杂度更高,从而更加安全。
3、使用HMAC技术
HMAC是一种基于哈希算法的消息认证码技术,它将密钥与消息进行混合计算,生成一个认证码,以此保证消息的完整性和真实性。HMAC技术可以在保证消息认证的同时,防止哈希长度拓展攻击。
4、使用较长的哈希值
较长的哈希值可以增加哈希长度拓展攻击的难度,因为攻击者需要计算更多的哈希值才能找到一个合法的哈希值。SHA-512和SHA-3等哈希算法提供了较长的哈希值选项。
5、使用加密哈希算法
加密哈希算法是一种特殊的哈希算法,它在计算哈希值的同时,还将密钥混合到哈希值中,从而保证了哈希值的安全性和不可逆性。常见的加密哈希算法包括HMAC-SHA256和bcrypt等。




