C128【?XXXX级】0311 ?组测试
欢迎到学校的OJ去切题QWQ
A - 修理牛棚 Barn Repair
这个题就非常的简单啊。首先，我们需要对牛棚里面的牛排个序。
然后，再计算出他们里面有的空隙（这样我们就可以让最长的木板长度短下来）。
最后，再从总的长度减去没有牛的地方就可以得到答案啦。
P.S. 这个题的标题是DP专题，折让机房某位神犇只得到了40分（不知道某人在标记题目的时候是怎么想的。反正我们都行习惯他的骚操作了）
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 210;
int m, s, c, tot;
int cow[N], no_use[N];
bool cmp(int a, int b)
{
return a > b;
}
int main()
{
freopen("barn1.in", "r", stdin);
freopen("barn1.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> m >> s >> c;
for(int i = 0; i < c; i++)
cin >> cow[i];
sort(cow, cow + c);
tot = cow[c - 1] - cow[0] + 1;
for(int i = 1; i < c; ++i)
no_use[i] = max(0, cow[i] - cow[i - 1] - 1);
sort(no_use + 1, no_use + c, cmp);
for (int i = 1; i <= m - 1 && i < c; ++i)
tot -= no_use[i];
cout << tot << endl;
return 0;
}
B - SR无敌1
显然答案不会超过3，因为只要前面翻转一下，后面翻转一下，再整体翻转一下就好了。答案是0和1很好判断，而当k=1，n-1,2,n-2时答案可能是2。直接手动构造一下即可。
我在这个地方是因为OJ可以看到部分题目数据看到自己缺了几种情况就给它加上了。
非常的不简单（没有人在考场上做对……）
#include <bits/stdc++.h>
using namespace std;
const int N = 100 + 10;
int a[N];
int n, k, cnt;
int main()
{
freopen("SR1.in", "r", stdin);
freopen("SR1.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> k;
if (k == 0)
{
cout << 0 << endl;
return 0;
}
else if (n == k)
{
cout << 1 << endl;
cout << 1 << " " << n << endl;
return 0;
}
else if (k == 1)
{
cout << 2 << endl;
cout << 1 << " " << n - k << endl;
cout << 1 << " " << n << endl;
return 0;
}
else if (n - k == 1.0 * n / 2)
{
cout << 3 << endl;
cout << 1 << " " << n / 2 << endl;
cout << n / 2 + 1 << " " << n << endl;
cout << 1 << " " << n << endl;
return 0;
}
else if (n - k > 1.0 * n / 2)
{
if (k == 2)
{
cout << 2 << endl;
cout << 1 << " " << 5 << endl;
cout << 2 << " " << n << endl;
}
else
{
cout << 3 << endl;
cout << n - k + 1 << " " << n << endl;
cout << 1 << " " << n - k << endl;
cout << 1 << " " << n << endl;
}
return 0;
}
else if (n - k < 1.0 * n / 2)
{
// cout << 2 << endl;
if (n - k == 1)
{
cout << 2 << endl;
cout << 2 << " " << n << endl;
cout << 1 << " " << n << endl;
}
else if (n - k == 2)
{
cout << 2 << endl;
cout << 2 << " " << n << endl;
cout << 1 << " " << n - 1 << endl;
}
else if (k >= 1.0 * n / 2)
{
cout << 3 << endl;
cout << 1 << " " << n - k << endl;
cout << n - k + 1 << " " << n << endl;
cout << 1 << " " << n << endl;
}
else
{
cout << 2 <<endl;
cout << 2 << " " << n << endl;
cout << 1 << " " << n - 1 << endl;
}
return 0;
}
return 0;
}
D - SR无敌2
不知道为什么老师会直接把某OI的题直接搬过来然后极草的改个名字就弄出来……
我是傻逼，贪心对了，模拟挂了。还在改中。
D - SR无敌3
像我这种蒟蒻就不配做这种题。题解没代码也看不懂。
我是傻逼。
E - COW Operations
这个题的题解有代码！
这个题有一个精髓：c可以变成ow，o可以变成cw，w可以变成co。
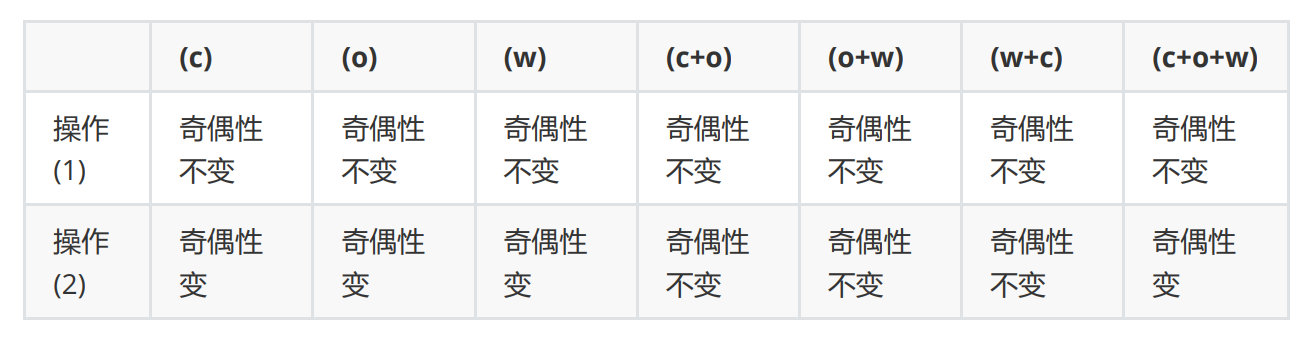
我们可以一起来看一下它的性质：
我们惊奇地发现：(c+o, o+w, w+c) 的奇偶性自始至终都不变！
既然我们需要把字符串变成单个字符 'C'，那么 (c+o) 就 (w+c) 就应该是奇数，(o+w) 就应该是偶数。
那么解法也呼之欲出了。我们使用前缀和维护 'c'，'o'，'w' 出现的次数，对于每一次询问，求出该子串里 (c+o, o+w, w+c) 的值，再判断奇偶性是否符合要求即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int pre[N][3];
int q, l, r, c, o, w, len;
char cow[N];
int main()
{
freopen("cow.in", "r", stdin);
freopen("cow.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> cow + 1;
len = strlen(cow + 1);
for (int i = 1; i <= len; i++)
{
if (i)
pre[i][0] = pre[i - 1][0], pre[i][1] = pre[i - 1][1], pre[i][2] = pre[i - 1][2];
if (cow[i] == 'C')
pre[i][0]++;
else if (cow[i] == 'O')
pre[i][1]++;
else
pre[i][2]++;
}
cin >> q;
while (q--)
{
cin >> l >> r;
if (l)
c = pre[r][0] - pre[l - 1][0], o = pre[r][1] - pre[l - 1][1], w = pre[r][2] - pre[l - 1][2];
else
c = pre[r][0], o = pre[r][1], w = pre[r][2];
if ((c + o & 1) && (c + w & 1) && !(o + w & 1))
cout << "Y";
else
cout << "N";
}
return 0;
}
解释一下，判断他们个数奇偶的地方的代码在干什么：判断区间[l, r]中是否存在COW子序列。具体来说，如果区间内C、O、W的个数都为奇数，且O和W的个数之和为偶数，则说明区间内一定存在COW子序列，输出'Y'；否则，说明区间内不存在COW子序列，输出'N'。其中，&表示按位与运算符，可以用来判断奇偶性。
