关于Tarjan

之前学Tarjan的时候一直理解不是很到位，温故而知新，查缺补漏一下。

Tarjan算法是用于求解有向图强连通分量的算法，它能做到线性时间的复杂度。

定义：

　　1.如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。

　　2.如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

 

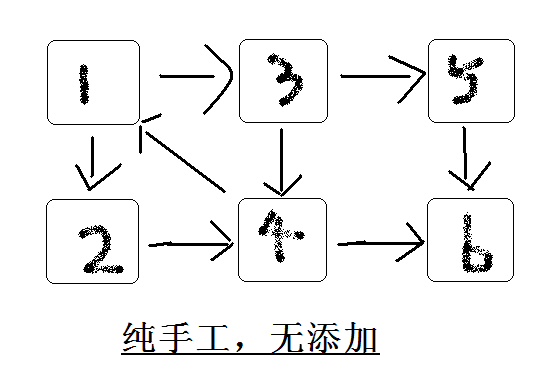
例如：在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

关于代码实现中的数组：

dfn[ i ] : 在DFS中该节点被搜索的次序(时间戳)

low[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当dfn[ i ]==low[ i ]时，为i或i的子树可以构成一个强连通分量。

模拟算法的实现：

以1为起始点：

 

 

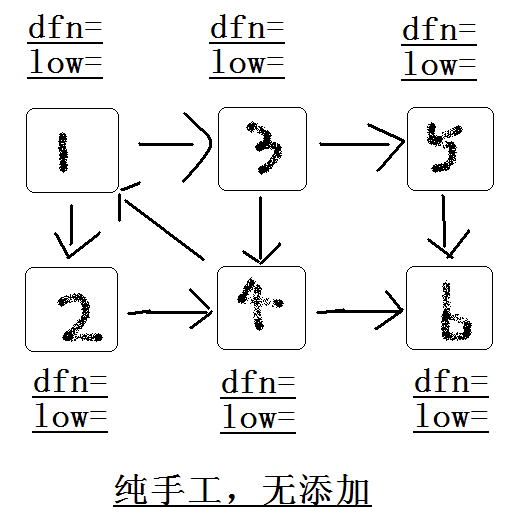
顺次DFS搜到节点6

 

 

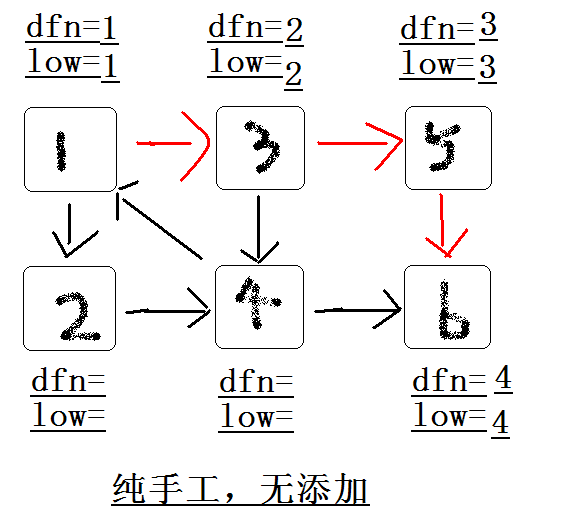
 回溯时发现low[ 5 ]==dfn[ 5 ] ,  low[ 6 ]==dfn[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

 

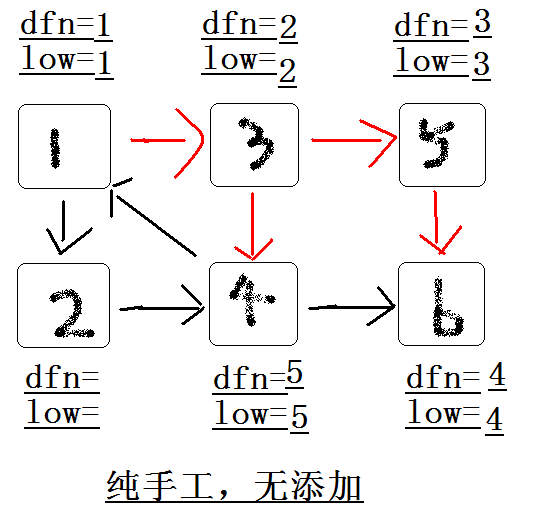
拓展节点1 ， 发现1再栈中更新low[ 4 ]，low[ 3 ] 的值为1

 

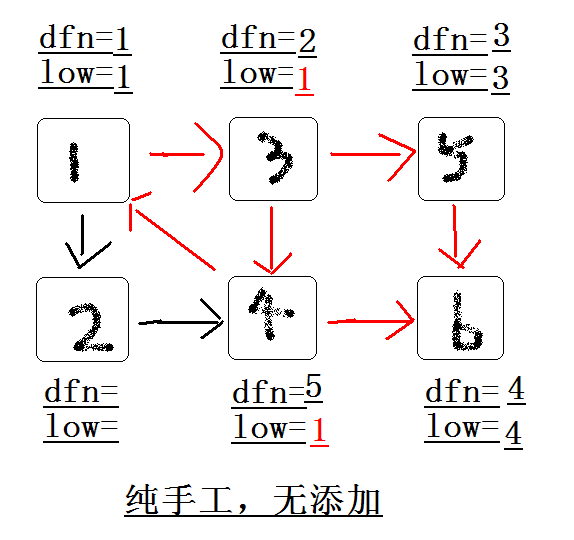
 回溯节点1，拓展节点2

 

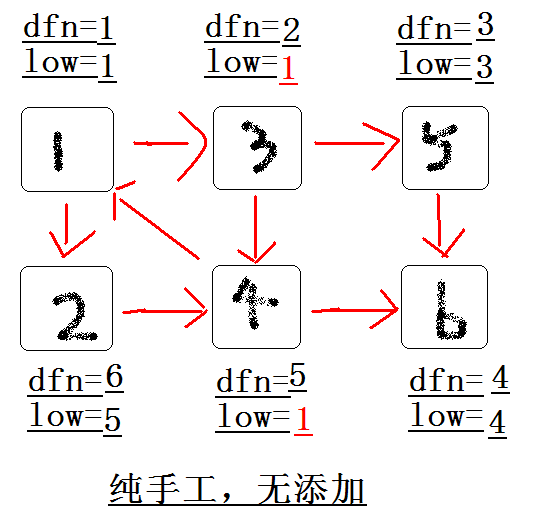
结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

 

时间复杂度为O(E+V)。

代码：

#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
struct node {
    int v,next;
} edge[1001];
int DFN[1001],LOW[1001];
int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y) {
    edge[++cnt].next=heads[x];
    edge[cnt].v = y;
    heads[x]=cnt;
    return ;
}
void tarjan(int x) { //代表第几个点在处理。递归的是点。
    DFN[x]=LOW[x]=++tot;// 新进点的初始化。
    stack[++index]=x;//进站
    visit[x]=1;//表示在栈里
    for(int i=heads[x]; i!=-1; i=edge[i].next) {
        if(!DFN[edge[i].v]) {//如果没访问过
            tarjan(edge[i].v);//往下进行延伸，开始递归
            LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
        } else if(visit[edge[i].v ]) { //如果访问过，并且还在栈里。
            LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
        }
    }
    if(LOW[x]==DFN[x]) { //发现是整个强连通分量子树里的最小根。
        do {
            printf("%d ",stack[index]);
            visit[stack[index]]=0;
            index--;
        } while(x!=stack[index+1]);//出栈，并且输出。
        printf("\n");
    }
    return ;
}
int main() {
    memset(heads,-1,sizeof(heads));
    int n,m;
    scanf("%d%d",&n,&m);
    int x,y;
    for(int i=1; i<=m; i++) {
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(int i=1; i<=n; i++)
        if(!DFN[i])  tarjan(i);//当这个点没有访问过，就从此点开始。防止图没走完
    return 0;
}

苦尽甘来。