关于树状数组

线段树和树状数组在noip中本人觉得挺重要的，而且比较难写。

我们先来看树状数组。

 

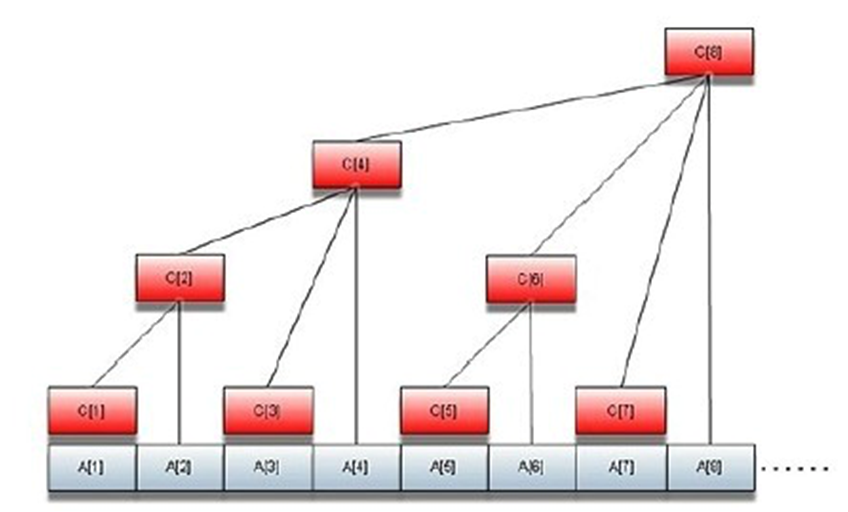
look at 这个图

 

那么我们会发现一个有趣的性质。

设节点编号为n，那么这个节点管辖的区间为2^k（其中k为n二进制末尾0的个数）个元素。

这个区间最后一个元素必然为An。

所以：Cn=A（n-2^k+1）+...An

神奇吧。

通常，我们管2^k叫做lowbit(n)，哇这个名字真好听。

计算方法呢就是n&（-n） 

原理呢就是计算机中的补码存储方式。->挺好的

关于查询：

这个时候我们要用到前缀和，通过查询前缀和来实现查询区间和。

那么我们如何实现呢，前缀和相减即可。

关于修改：

代码：（add与query）

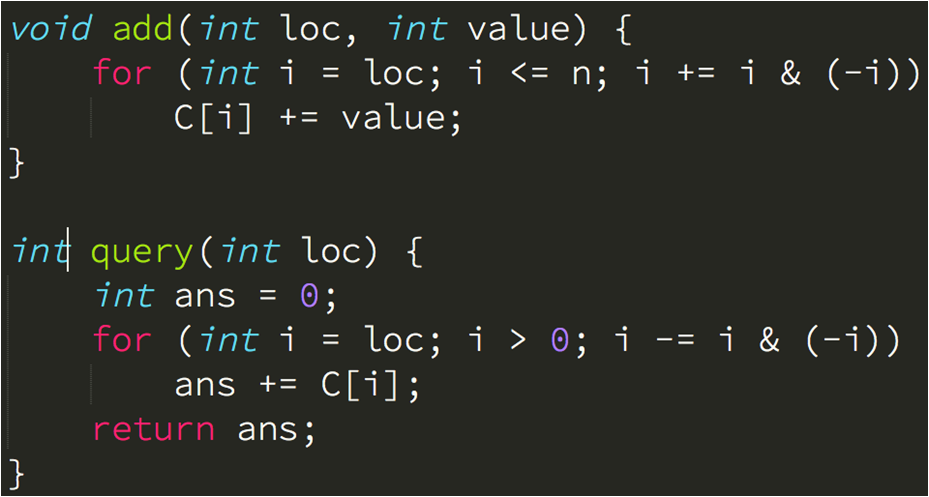
众所周知（在我看来），树状数组不论是空间还是时间，都是完胜线段树的，那么我们就来分析一下它的复杂度：

1.查询的时候，因为每次都会让二进制表示中的最后一个1变为0，所以是O（log₂n）。

2.修改的时候，同样也是每次让二进制表示中的最后一个1变为0，所以是O(log₂n)。

相比于其他大型数据结构如线段树啊，splay啊，他在常数上非常有优势。

不过缺点是，他的应用面比较窄，基本是只能维护数字之后这一种信息。你可以在各大网站的模板题中看出来。

代码实现：

洛谷 模板1

#include<cstdio>
#include<iostream>
int n,m,a[500010];
void add(int l,int r) {
    while(l<=n) a[l]+=r,l+=l&(-l);
}
int sum(int x) {
    int num=0;
    while(x) num+=a[x],x-=x&(-x);
    return num;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int x,i=1;i<=n;i++) 
        scanf("%d",&x),add(i,x);
    for(int i=1,a,b,c;i<=m;i++){
        scanf("%d%d%d", &a, &b, &c);
        if(a==1) add(b,c);
        else printf("%d\n",sum(c)-sum(b-1));
    }
    return 0;
}

洛谷 模板2

#include <iostream>
#include <cstdio>
#define lowbit(x) x & -x
using namespace std;
long long tree[500005];
int n, m;
void add(int x, long long num) {
    while (x <= n) {
        tree[x] += num;
        x += lowbit(x);
    }
}
long long query(int x) {
    long long ans = 0;
    while (x) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
int main() {
    freopen("in.txt", "r", stdin);
    scanf("%d%d", &n, &m);
    long long last = 0, now;
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &now);
        add(i, now - last);
        last = now;
    }
    int flg;
    while (m--) {
        scanf("%d", &flg);
        if (flg == 1) {
            int x, y;
            long long k;
            scanf("%d%d%lld", &x, &y, &k);
            add(x, k);
            add(y + 1, -k);
        } else if (flg == 2) {
            int x;
            scanf("%d", &x);
            printf("%lld\n", query(x));
        }
    }
    return 0;
}

 

上面我们讨论了一维的，下面我们来讨论一下二维的。

 

其实很简单，就是树状数组套树状数组。

 

代码：

 

 

具体实现：

 

Mobile phones

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 1100
int n,c[N][N];
inline int lowbit(int x){
    return x&-x;
}
void updata(int x,int y,int v){
    for(int i=x;i<=n;i+=lowbit(i)){
        for(int j=y;j<=n;j+=lowbit(j)){
            c[i][j]+=v;
        }
    }
}
int sum(int x,int y){
    int res=0;
    for(int i=x;i;i-=lowbit(i)){
        for(int j=y;j;j-=lowbit(j)){
            res+=c[i][j];
        }
    }
    return res;
}
int getsum(int x1,int y1,int x2,int y2){
     return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1);
}
int main(){
    int opt,l,r,x,y,a,b,t;
    while(scanf("%d",&opt)!=EOF){
        if(opt==0){
            scanf("%d",&n);
            memset(c,0,sizeof(c));
        }
        else if(opt==1){
            scanf("%d%d%d",&x,&y,&a);
            updata(x+1,y+1,a);
        }
        else if(opt==2){
            scanf("%d%d%d%d",&l,&b,&r,&t);
            printf("%d\n",getsum(l+1,b+1,r+1,t+1));
        }
    }
    return 0;
}

总结：树状数组作为一种方便、高效的数据结构，通常和其它的一些算法一起使用，而将树状数组作为主算法的题目反而较少。熟练掌握树状数组，是每个选手想要成功应该做到的。

下一篇我们要讲树状数组的升级版，线段树，拥有比树状数组更强大的功能，而且比较好理解，只不过更繁琐一些，在复杂度方面不如树状数组。

 

一世安宁