关于主席树
按老师说的,他第一次见到可持久化数据结构的时候,觉得它很神奇(其实只是没见过世面而已)。
主席树,这个名字是怎么来的呢?
原因,学长是这样说的:因为发明这种数据结构的大佬名字缩写和hjt主席一样,于是,便叫主席树。
下面进入正文:
主席树,又称函数式线段树、可持久化线段树。
传说是一位大神没学会划分树,于是发明了这个数据结构,作为替代品。
想要学会主席树,首先你要会线段树,前缀和思想。
既然你点开了这篇博客,那你肯定是会线段树的,不会我也没办法,下次写,至于为什么先写主席树再写线段树,,嗯,,一时兴起。
前缀和思想,这比较基础了吧,如果你不会,那你白学到这里了。
首先我们看一道题目:
给出100000个数,向你提5000问,L到R间的第K大数是多少?
我们首先想到的那肯定是暴力啊!
最为一个暴力选手这个时候就不得不说一句了,我最爱暴力了。
但是一看数据范围,肯定不行啊。
线段树?
k值是不变的,你怎么写??
滑动窗口+单调队列?
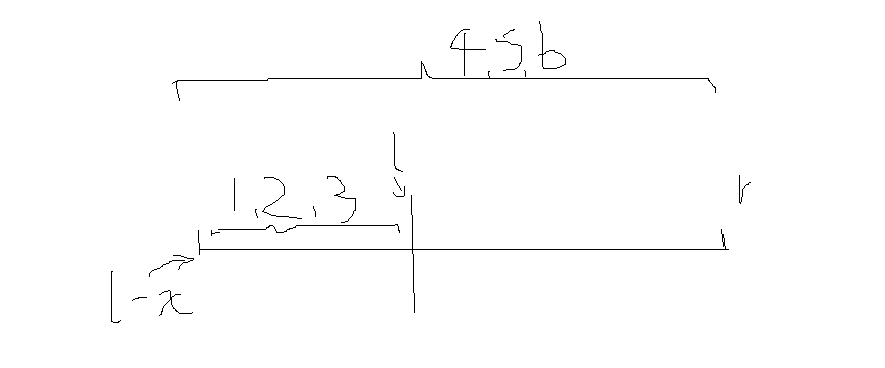
画画这种东西,不能强求对吧,画的丑我也不愿意。
如果是上面一种情况,l-x到l最大的三个值是1.2.3,l-x到r最大的三个值是4.5.6我们可以清晰地知道l到r之间最大的三个值是4.5.6.
单如果把4改成3呢?
你还能确定3是l到r里的?
那么接下来,我们需要我们亲爱的主席树了。
要知道第k大的值就要维护k个值,然后用前缀和的思想。
but刚刚就说了要线段树,我们先看线段树。
建立n+1棵线段树,统计每个数到sz[i]时的出现次数。那么线段树R比线段树L-1多出来的数中的第K大就是答案。
那么问题来了: 数字如果太大,线段树是装不下的(因为求和啊)
解决的方法: 把所有的数排序、去重,线段树中存储的不是数本身而是数字的排序。
就是给他们一些编号,而且还快呢。
然后,空间,n+1棵线段树。一棵线段树需要开到n*4,那这不是要开到(n+1)n*4????
这显然是不客观的。
那么!我们主席树的神奇之处就体现出来了!
我们可以用公用节点。
建立的过程:
1、数组排序、去重
sz: 2 4 6 8 8 6 4 2
hash:2 4 6 8
用hash的值对sz内的值进行更改变为
sz: 1 2 3 4 4 3 2 1
代码:
for(int i=1; i<=n; ++i) { readint(sz[i]); hash[i]=sz[i]; } sort(hash+1,hash+n+1); int siz=unique(hash+1,hash+n+1)-hash-1; for(int i=1; i<=n; ++i) sz[i]=lower_bound(hash+1,hash+siz+1,sz[i])-hash;
2、建立root[0]
依照排序去重后的点数建立线段树
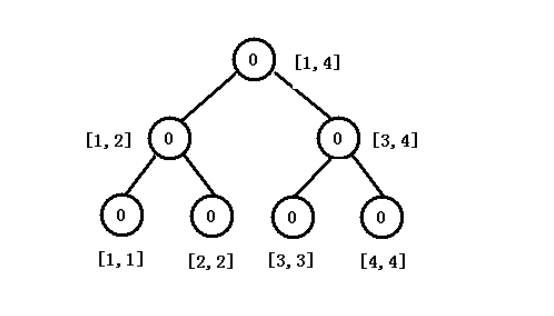
[x,y]表示x到y的区间。
代码:
build(root[0],1,siz); void build(node * &cur,int l,int r) { cur=(node *)malloc(sizeof(node)); cur->cnt=0; cur->ch[0]=cur->ch[1]=NULL; cur->l=l; cur->r=r; if(l!=r) { int mid=(l+r)/2; build(cur->ch[0],l,mid); build(cur->ch[1],mid+1,r); } }
3、建立root[1]~root[n](依照数列的大小建立)
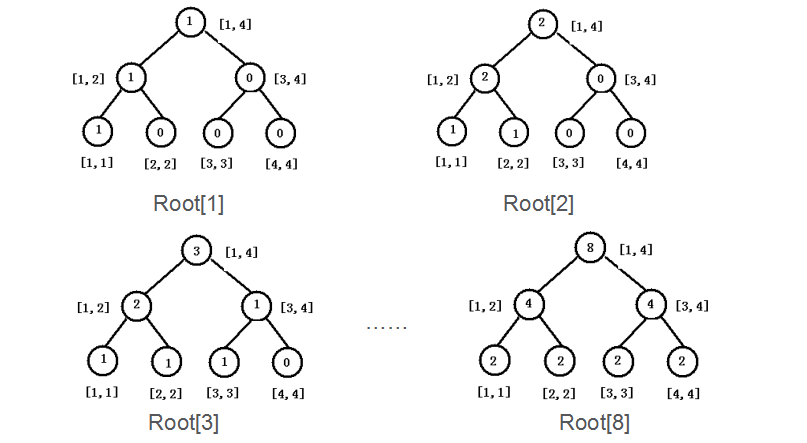
代码:
void update(node * pre,int ps,node * &cur,int l,int r) { cur=(node *)malloc(sizeof(node)); cur->cnt=pre->cnt+1; cur->l=pre->l; cur->r=pre->r; cur->ch[0]=pre->ch[0]; cur->ch[1]=pre->ch[1]; if(l==r)return ; int mid=(l+r)/2; if(ps<=mid)update(pre->ch[0],ps,cur->ch[0],l,mid); else update(pre->ch[1],ps,cur->ch[1],mid+1,r); } for(int i=1; i<=n; ++i) update(root[i-1],sz[i],root[i],1,siz);
4、查询
以l,r,k分别为3、8、3为例
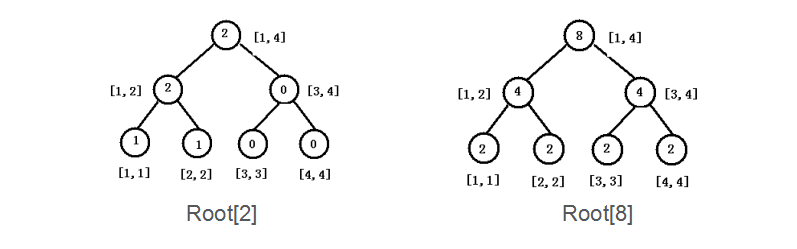
root[8]的左孩子-root[2]左孩子为2,说明第3大在右孩子中,查询右孩子的k-2=1;
root[8]的右孩子的左孩子比root[2]的右孩子的左孩子大2,所以在root的右孩子的左孩子中,而此时已经到叶子,返回当前叶子的序号3。
所以3到8的第3大孩子为hash[3]=6。
代码:
int query(node * lt,node *rt,int l,int r,int k) { if(l==r)return l; int mid=(l+r)/2,cha=rt->ch[0]->cnt - lt->ch[0]->cnt; if(k<=cha)return query(lt->ch[0],rt->ch[0],l,mid,k); else return query(lt->ch[1],rt->ch[1],mid+1,r,k-cha); }
5、节省空间的实际建图
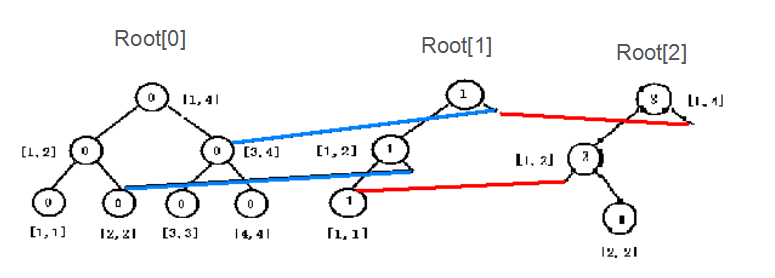
提醒一下:
空间为n*4+n*logn 不过要用数组模拟指针,不然你一遍遍用指针开空间,会MLE。
以下为数组模拟代码:
嘻嘻可甜可盐
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define MAXN 100001 using namespace std; int n,m,root[MAXN],cut,a[MAXN],s[MAXN],t,x,y,z; struct data { int lc,rc,ans; } tree[MAXN*20]; void add(int &now,int last,int l,int r,int x) { now=++cut; tree[now].ans=tree[last].ans+1; tree[now].lc=tree[last].lc,tree[now].rc=tree[last].rc; if(l==r) return ; int mid=(l+r)>>1; if(x<=mid) add(tree[now].lc,tree[last].lc,l,mid,x); else add(tree[now].rc,tree[last].rc,mid+1,r,x); return ; } int query(int L,int R,int l,int r,int x) { if(l==r) return l; int p=tree[tree[R].lc].ans-tree[tree[L].lc].ans; int mid=(l+r)>>1; if(p>=x) return query(tree[L].lc,tree[R].lc,l,mid,x); else return query(tree[L].rc,tree[R].rc,mid+1,r,x-p); } int main() { while(scanf("%d%d",&n,&m)!=EOF) { cin>>n>>m; cut=0; memset(root,0,sizeof root); for(int i=1; i<=n; i++) cin>>s[i]>>s[i]; sort(s+1,s+n+1); for(int i=1; i<=n; i++) { int p=lower_bound(s+1,s+n+1,a[i])-s; add(root[i],root[i-1],1,n,p); } while(m--) { cin>>x>>y>>z; int p=query(root[x-1],root[y],1,n,z); printf("%d\n",s[p]); } } return 0; }
一世安宁


 浙公网安备 33010602011771号
浙公网安备 33010602011771号