洛谷 P1350 车的放置
洛谷 P1350 车的放置
题目描述
有下面这样的一个网格棋盘，a，b，c，d表示了对应边长度，也就是对应格子数。
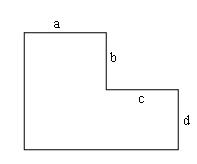
当a=b=c=d=2时，对应下面这样一个棋盘
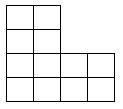
要在这个棋盘上放K个相互不攻击的车，也就是这K个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。同样只需要输出答案mod 100003后的结果。
输入输出格式
输入格式：
输入文件place.in的第1行为有5个非负整数a, b, c, d和k。
输出格式：
输出文件place.out包括1个正整数，为答案mod 100003后的结果。
输入输出样例
说明
【数据规模与约定】
对于部分数据，有b = 0；
对于部分数据，有a，b，c，d≤4。
对于100%的数据，a，b，c，d，k≤1000，且保证了至少有一种可行方案。
题解：
f[j][i]=(f[j-1][i]+f[j-1][i-1]*(v[j]-i+1))%MOD;
因为题目里提到最终数据要模去100003
所以定义MOD为100003了。
以下代码
1 #include<cstdio> 2 const int N=1005; 3 const int MOD=100003; 4 int f[N][N],v[N]; 5 int x,y,z,k,m,ans; 6 inline int read() { 7 char c=getchar(); 8 int f=1,x=0; 9 while(c<'0'||c>'9') { 10 if(c=='-') f=-1; 11 c=getchar(); 12 } 13 while(c>='0'&&c<='9') 14 x=x*10+c-48,c=getchar(); 15 return x*f; 16 } 17 void print (int x) { 18 if(x<0) { 19 putchar('-'); 20 x=-x; 21 } 22 if(x>9) { 23 print(x/10); 24 } 25 putchar(x%10+'0'); 26 } 27 int main() { 28 // x=y=z=k=m=read(); 29 scanf("%d%d%d%d%d",&x,&y,&z,&k,&m); 30 for(int i=1; i<=z; i++) v[i]=k,f[i][0]=1; 31 for(int i=1; i<=x; i++) v[z+i]=k+y,f[z+i][0]=1; 32 f[0][0]=1; 33 for(int j=1; j<=x+z; j++) 34 for(int i=1; i<=m; i++) 35 f[j][i]=(f[j-1][i]+f[j-1][i-1]*(v[j]-i+1))%MOD; 36 ans=f[x+z][m]; 37 // print(ans); 38 printf("%d",ans); 39 return 0; 40 }
不知道为什么，加了读入优化和输出优化，虽然过样例是没问题的，但是在提交的时候不是re就是wa。
然后我把读入输出优化去掉，还故意把数组弄小了，都比之前数组开大了得分高!
所以肯定是优化的原因啊！
一世安宁
