关于拓扑排序
拓扑排序
英文名称:Topological-sort
别称:toposort or topsort
以下进入胡扯时间 正题:
排序???
a:我有sort!
b:我还会桶排!
c:我我我!我还会基数排序和计数排序
哇塞!厉害!
但是你会这些东西和我拓扑排序有什么关系
a??b??c???
拓扑排序是干什么的呢
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
以上来自360百科
看明白了吗,反正我是不想看
嗯!这才是正题。
首先,我们由一个小问题引入。
有这么一群人,小红爱着小绿,她得亲眼看着小绿吃完饭她才会安心吃饭,
而这个时候,小黄也爱着小绿,他也要亲眼看着小绿把饭吃完她才会安心。
同时,小蓝爱着小红和小黄,她得亲眼看着小红和小黄吃完饭她才可以吃饭,
而小紫是个基佬,他不爱小红,不爱小黄,不爱小蓝,也不爱小绿,正因为他是基佬所以他对小红小黄毫无威胁性,
于是小紫可以同小绿一起吃饭,当然也不可以不。
那么最终,大家吃饭的顺序是怎样的呢。
形象一点,画个图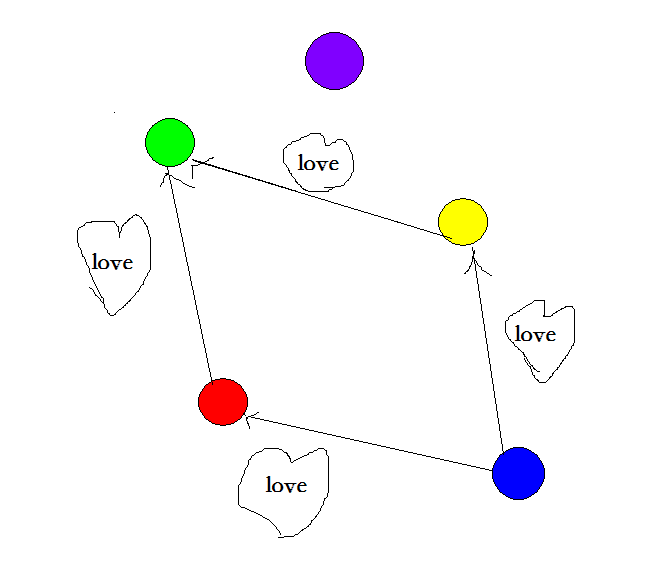
大佬们看到这个小问题:这个sb题!这不是分分钟秒切的事情吗!
像我这种小菜鸡:诶??爆搜吗?
爆搜??什么zz做法。别说,还真有点意思。
不过我们首先讲的,是Kahn算法,一看这个算法就很高级对不对!
对什么对,只是听起来高级而已。
其算法主要流程如下:
1.从图中找到一个入度为零的点,并输出
2.在图中删去和这个点相连的所有边,再重复1的操作
3.一直重复1.2的操作一直到图中不再有入度不为零的点为止。
当然,如果图中有环那是无解的。
那么它的复杂度是多少呢?
你猜你猜你猜
证明:初始化入度为0的集合需要遍历整张图,检查每个节点和每条边,对该集合进行操作,又需要遍历整张图中的,每条边,则复杂度为O(E+V);
代码:
#include<stack> #include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn = 1000 + 10; const int INF = 1e9 + 7; int T, n, m, num[maxn]; vector<int> vis[maxn], v; stack<int> s; void topo() { for(int i = 1; i <= n; i++) if(num[i] == 0) s.push(i); while(!s.empty()) { int now = s.top(); v.push_back(now); s.pop(); for(int j = 0; j < vis[now].size(); j++) if((--num[vis[now][j]]) == 0) s.push(vis[now][j]); } if(v.size() != n) cout << "NO solution" << '\n'; else for(int i = 0; i < v.size(); i++) cout<<v[i]<<" "; } int main() { scanf("%d%d", &n, &m); for(int i = 0; i <= n; i++) vis[i].clear(); memset(num, 0, sizeof(num)); for(int i = 0, u, v; i < m; i++) scanf("%d%d", &u, &v), vis[u].push_back(v), num[v]++; topo(); return 0; }
现在我们再来讲基于DFS的算法
需要注意的是,将顶点添加到结果anst中的时机是在vis方法即将退出之时。
搜索嘛,实践略简单,但是理解上要下点功夫。
其关键在于为什么在vis方法的最后将该顶点添加到一个集合中,就能保证这个集合就是拓扑排序的结果?
因为添加顶点到集合中的时机是在dfs方法即将退出之时,而dfs方法本身是个递归方法,只要当前顶点还存在边指向其它任何顶点,它就会递归调用dfs方法,而不会退出。因此,退出dfs方法,意味着当前顶点没有指向其它顶点的边了,即当前顶点是一条路径上的最后一个顶点。
那么问题来了,这个方法对吗?
你猜你猜你猜
证明:
考虑任意的边,当调用dfs(v)的时候,有三种情况:
- dfs(w)还没有被调用,即所要走的点还未走,此时会调用dfs(w),然后当dfs(w)返回之后,dfs(v)才会返回
- dfs(w)已经被调用并返回了,即w已经被mark
- dfs(w)已经被调用但是在此时调用dfs(v)的时候还未返回
需要注意的是,以上第三种情况在拓扑排序的场景下是不可能发生的,因为如果情况3是合法的话,就表示存在一条由w到v的路径。而现在我们的前提条件是由v到w有一条边,这就导致我们的图中存在环路,从而该图就不是一个有向无环图(DAG),而我们已经知道,非有向无环图是不能被拓扑排序的。
那么考虑前两种情况,无论是情况1还是情况2,w都会先于v被添加到结果列表中。所以边v->w总是由结果集中后出现的顶点指向先出现的顶点。为了让结果更自然一些,可以使用栈来作为存储最终结果的数据结构,从而能够保证边v->w总是由结果集中先出现的顶点指向后出现的顶点。
时间复杂度:
证明:DFS遍历一遍的时间为O(E+V),而记录结果的时间花费为O(1),所以总时间复杂度为O(E+V)
代码:
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 1000 + 10;
const int INF = 1e9 + 7;
int n, m, dis[maxn], ans[maxn], t;
vector<int> vis[maxn];
bool dfs(int u) {
dis[u] = -1;
for(int i = 0; i < vis[u].size(); i++) {
int v = vis[u][i];
if(dis[v] < 0) return false;
else if(!dis[v] && !dfs(v)) return false;
}
dis[u] = 1, ans[--t] = u;
return true;
}
bool toposort() {
t = n;
memset(dis, 0, sizeof(dis));
for(int u = 1; u <= n; u++)
if(!dis[u]) if(!dfs(u)) return false;
return true;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i++) vis[i].clear();
for(int i = 0, u, v; i < m; i++)
scanf("%d%d", &u, &v), vis[u].push_back(v);
if(toposort()) for(int i = 0; i < n; i++) printf("%d ",ans[i]);
else puts("NO solution");
return 0;
}
一世安宁


 浙公网安备 33010602011771号
浙公网安备 33010602011771号