luogu P2762 太空飞行计划问题
好像是最大权闭合图,也就是最大流最小割啦,找出最大流的路径输出,这题如何建模呢,一样的先设源点和汇点,源点向每个计划连capacity为赞助数的边,每个计划连相应装置capacity为无穷的边,每个装置向汇点连capacity为支付费用的边,这样,最大利润就是赞助总数-最大流啦,如何证?看两个例子
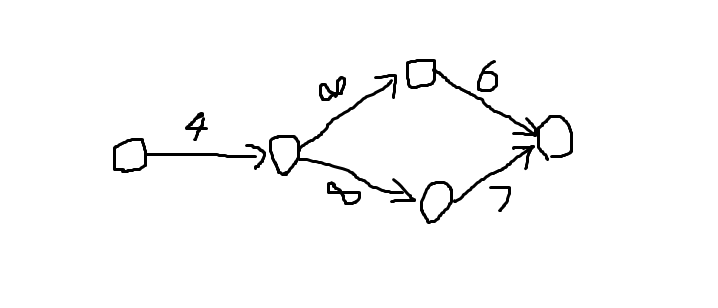
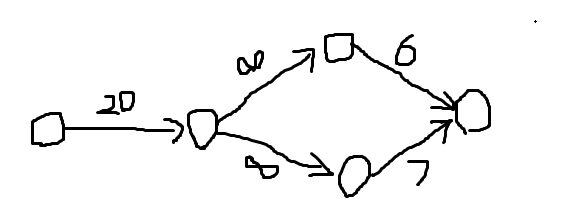
若是可行方案,相减即为利润,若是不可行方案,相减就为0,数学归纳法可推知n个时也对
另一个问题,如何找到最大权闭合图呢,最后一次分层的level数组就可以帮忙了,我们知道退出dinic算法就是无法到达汇点,考虑如何分层,满足两个条件,capacity大于flow且尚未分层,我们知道,对答案有贡献的是到计划的那条边的capacity比其相应的装置的capacity加起来还要大,最后一次分层时,即已经达到最大流,若从源点到某个计划无法分层,说明其capacity<=对应装置的,那就一定不选,能分层的一定是源有余而汇不进,又计划和装置之间的流量是无穷,则一定可以分层,直接考虑最后一层的level数组并输出即可,附上别个大佬的解释(


#include<bits/stdc++.h> using namespace std; #define lowbit(x) ((x)&(-x)) typedef long long LL; const int maxm = 1e4+5; const int INF = 0x3f3f3f3f; struct edge{ int u, v, cap, flow, nex; } edges[maxm]; int head[maxm], cur[maxm<<1], cnt, level[105], give[55], cost[55]; vector<int> req[55]; void init() { memset(head, -1, sizeof(head)); } void add(int u, int v, int cap) { edges[cnt] = edge{u, v, cap, 0, head[u]}; head[u] = cnt++; } void addedge(int u, int v, int cap) { add(u, v, cap), add(v, u, 0); } void bfs(int s) { memset(level, -1, sizeof(level)); queue<int> q; level[s] = 0; q.push(s); while(!q.empty()) { int u = q.front(); q.pop(); for(int i = head[u]; i != -1; i = edges[i].nex) { edge& now = edges[i]; if(now.cap > now.flow && level[now.v] < 0) { level[now.v] = level[u] + 1; q.push(now.v); } } } } int dfs(int u, int t, int f) { if(u == t) return f; for(int& i = cur[u]; i != -1; i = edges[i].nex) { edge& now = edges[i]; if(now.cap > now.flow && level[u] < level[now.v]) { int d = dfs(now.v, t, min(f, now.cap - now.flow)); if(d > 0) { now.flow += d; edges[i^1].flow -= d; return d; } } } return 0; } int dinic(int s, int t) { int maxflow = 0; for(;;) { bfs(s); if(level[t] < 0) break; memcpy(cur, head, sizeof(head)); int f; while((f = dfs(s, t, INF)) > 0) maxflow += f; } return maxflow; } void run_case() { init(); int n, m; scanf("%d%d", &m, &n); char in[10005]; int s = 0, t = m+1+n, sum = 0; for(int i = 1; i <= m; ++i) { scanf("%d", &give[i]); sum += give[i]; memset(in, 0, sizeof(in)); cin.getline(in, 10000); int ulen = 0, num; while(sscanf(in+ulen, "%d", &num) == 1) { req[i].push_back(num); if(num == 0) ulen++; else while(num) { num /= 10; ulen++; } ulen++; } } for(int i = 1; i <= n; ++i) scanf("%d", &cost[i]); for(int i = 1; i <= m; ++i) { addedge(s, i, give[i]); for(int j = 0; j < req[i].size(); ++j) addedge(i, m+req[i][j], INF); } for(int i = 1; i <= n; ++i) addedge(i+m, t, cost[i]); int ans = sum - dinic(s, t); for(int i = 1; i <= m; ++i) { if(level[i] != -1) printf("%d ", i); } printf("\n"); for(int i = 1; i <= n; ++i) if(level[i+m] != -1) printf("%d ", i); printf("\n%d", ans); } int main() { ios::sync_with_stdio(false), cin.tie(0); run_case(); //cout.flush(); return 0; }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号