luogu P4129 [SHOI2006]仙人掌
题目描述
仙人掌图(cactus)是一种无向连通图,它的每条边最多只能出现在一个简单回路(simple cycle)里面。从直观上说,可以把仙人掌图理解为允许存在回路的树。但是仙人掌图和树之间有个本质的不同,仙人掌图可以拥有多个支撑子图(spanning subgraph),而树的支撑子图只有一个(它自身),我们把仙人掌图的支撑子图的数目称为“仙人数”。你的任务就是计算给定图的“仙人数”。
一些关于仙人掌图的举例:
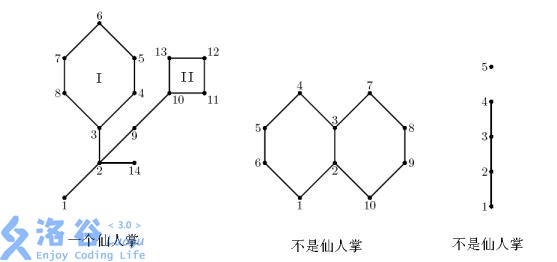
第一张图是一个仙人掌图,第二张图的边(2,3)在两个不同的回路里面,所以不是仙人掌图,第三张图不是一个连通图,所以也不是仙人掌图。
以下是对一些术语的解释:
简单回路(simple cycle):简单回路是原图的一条路径,这条路径的边集构成了回路,回路中顶点只能出现一次。比如对于上例中第二个图来说,它一共有三个简单回路,分别是(4,3,2,1,6,5)、(7,8,9,10,2,3)和(4,3,7,8,9,10,2,1,6,5)
支撑子图(spanning subgraph):支撑子图也是原图的子图,这种子图可以比原来少一些边,但是不能破坏图的连通性,也不能去除原来图上的任何顶点。“支撑”的概念类似于我们熟知的“最小支撑树”,对于上例中的第一张图来说,任意去除回路I中的图或回路II中的一条边都能构成一个支撑子图,所以它的支撑子图一共有6 + 4 + 6 × 4 + 1 = 35种(注意图自身也是自己的一个子图)
输入格式
输入文件的第一行是两个整数n和m(1≤n≤20000, 0≤m≤1000)。n代表图的顶点数,顶点的编号总是从1到n表示的。
接下来一共有m行。每行都代表了图上的一条路径(注意:这里所表示的一条路径可不一定是一条回路)。这些行的格式是首先有一个整数ki(2≤ki≤1000)代表这条路径通过了几个顶点,接下来是ki个在1到n之间的数字,其中每个数字代表了图上的一个顶点,相邻的顶点之间就定义了一条边。一条路径上可能通过一个顶点好几次,比如对于第一个例子,第一条路径从2经过3,又从8返回到了3,但是我们保证所有的边都会出现在某条路径上,而且不会重复出现在两条路径上,或者在一条路径上出现两次。
输出格式
输出这张图的“仙人数”,如果它不是一张仙人掌图,输出0。注意最后的答案可能是一个很大很大的数。
输入输出样例
14 3 9 1 2 3 4 5 6 7 8 3 7 2 9 10 11 12 13 10 2 2 14
35
10 2 7 1 2 3 4 5 6 1 6 3 7 8 9 10 2
0
5 1 4 1 2 3 4
0
思路:注意高精度和与点双不同的是判简单环边数即可

typedef long long LL; typedef pair<LL, LL> PLL; const LL bas = 100000000; struct Big_Number { LL a[1000],len; void init() { len = 1; memset(a, 0, sizeof a); a[0] = 1; } void mul(LL val) { for (int i = 0; i < len; i++) { a[i] = a[i] * val; } for (int i = 0; i < len; i++){ a[i + 1] += a[i] / bas; a[i] %= bas; } while (a[len]) { a[len + 1] = a[len] / bas; a[len] %= bas; len++; } } void print() { printf("%lld", a[len - 1]); for (int i = len - 2; i >= 0; i--) { printf("%.8lld", a[i]); } printf("\n"); } } ans; const int maxm = 2e6+5; const int maxn = 2e5+5; int head[maxm], edgecnt, dfn[maxn], low[maxn], bcc_cnt, bccnum[maxn], dfs_clock, s[maxm], top, vis[maxn], num; LL bcc[maxn]; bool ok = true; struct edge{ int u, v, nex; } edges[maxm]; void addedge(int u, int v) { edges[++edgecnt].u = u; edges[edgecnt].v = v; edges[edgecnt].nex = head[u]; head[u] = edgecnt; } void dfs(int u, int fa) { vis[u] = 1; ++num; for(int i = head[u]; i; i = edges[i].nex) { int v = edges[i].v; if(v == fa) continue; if(!vis[v]) dfs(v, u); } } void tarjan(int u, int fa) { dfn[u] = low[u] = ++dfs_clock; int child = 0, v; for(int i = head[u]; i; i = edges[i].nex) { v = edges[i].v; if(v == fa) continue; if(!dfn[v]) { s[++top] = i; tarjan(v, u); low[u] = min(low[u], low[v]); if(low[v] >= dfn[u]) { ++bcc_cnt; LL vet = 0; while(true) { int num = s[top--]; if(bccnum[edges[num].v] != bcc_cnt) { vet++; bccnum[edges[num].v]=bcc_cnt; } else ok = false; if(edges[num].u == u && edges[num].v == v) break; } if(ok && vet>1) ans.mul(vet+1); } } else if(dfn[v] < dfn[u]){ s[++top] = i; low[u] = min(low[u], dfn[v]); } } } void run_case() { int n, m, u, v, t; ans.init(); cin >> n >> m; for(int i = 1; i <= m; ++i) { cin >> t; t--; cin >> u; while(t--) { cin >> v; addedge(u, v), addedge(v, u); u = v; } } dfs(n, -1); if(n != num) { cout << "0"; return; } tarjan(1, -1); if(!ok) cout << "0"; else ans.print(); } int main() { //ios::sync_with_stdio(false), cin.tie(0); run_case(); return 0; }
(自用板,记录每一个点双和割点





