学习进度

7.1数值微分与数值积分

一、数值微分

1、数值差分与差商：微积分中，任意函数f(x)在x0点的导数是通过极限定义的：

 

 

 

如果去掉极限定义中h趋向于0的极限过程，得到函数在x0点处以h（h>0）为步长的向前差分、向后差分和中心差分公式：

向前差分：

 

 

 

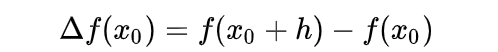
向后差分：

 

 

 

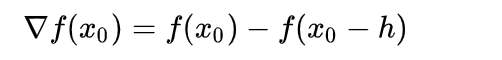
中心差分：

 

 

 

 

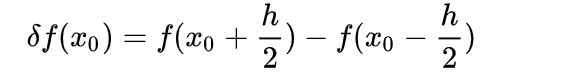
函数f(x)在点x0的微分接近于函数在该点的差分，而f在点x的导数接近于函数在该点的差商。

差商亦可以如下公式求出：

一阶差商：

 

 

 

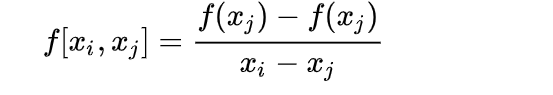
二阶差商：

 

 

 

 

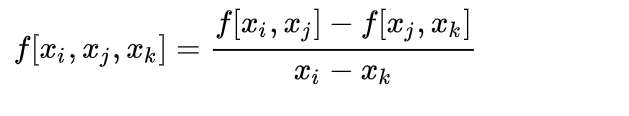
2、数值微分的实现：MATLAB提供了求向前差分的函数diff，其调用格式有三种：

dx=diff(x)：计算向量x的向前差分，dx(i)=x(i+1)-x(i)，i=1，2，…，n-1。

dx=diff(x,n)：计算向量x的n阶向前差分。例如，diff(x,2)=diff(diff(x))。

dx=diff(A,n,dim)：计算矩阵A的n阶差分，dim=1时（默认状态），按列计算差分；dim=2，按行计算差分。

注意：diff函数计算的是向量元素间的差分，故差分向量元素的个数比原向量少了一个。同样，对于矩阵来说，差分后的矩阵比原矩阵少了一行或一列。 另外，计算差分之后，可以用f(x)在某点处的差商作为其导数的近似值。

e.g. 设f(x)=sinx在[0，2π]范围内随机采样，计算f'(x)的近似值，并与理论值f'(x)=cosx进行比较。

代码：>> x=[0,sort(2*pi*rand(1,5000)),2*pi];   //取[0,2π]内随机数，并按从小到大顺序排列

>> y=sin(x);   //做原函数y=sin(x)

>> f1=diff(y)./diff(x);  //求x，y的一阶向前差分，并求出差商向量f1

>> f2=cos(x(1:end-1));   //求差商向量的理论值f2

>> plot(x(1:end-1),f1,x(1:end-1),f2);   //绘制f1、f2的曲线

>> d=norm(f1-f2)  //求出f1与f2之差