无用技巧总结
一、cmd中常用命令总结
这些命令是 cmd 中最常用的命令之一,但未必是全部命令的完整列表。是否可以使用这些命令也可能取决于您所使用的特定操作系统的版本、安全设置等因素。
在Windows操作系统中,copy 是一个命令行实用程序,用于将文件从一个位置复制到另一个位置。
以下是在命令提示符窗口中使用 copy 命令的基本用法:
- 将一个文件从一个位置复制到另一个位置:
copy 源文件 目标文件
例如,将"myfile.txt"文件从"C:\folder1"复制到"C:\folder2",则命令如下:
copy C:\folder1\myfile.txt C:\folder2\myfile.txt
- 将多个文件复制到一个目录:
例如,将"C:\folder1\file1.txt"和"C:\folder1\file2.txt"文件复制到"C:\folder2",则命令如下:
- 复制一个目录及其子目录和文件:
xcopy 源目录 目标目录 /e
例如,将"C:\folder1"目录及其子目录和文件复制到"C:\folder2",则命令如下:
xcopy C:\folder1 C:\folder2 /e
这些是最基本的copy命令用法,可以使用命令行参数来配置更多选项。可以在命令提示符窗口中输入"copy /?"或"xcopy /?",以获取更多帮助信息。
在命令提示符(cmd)窗口中,可以使用以下命令创建一个新文件:
其中,"filename.txt"是你想创建的文件名。这将创建一个空文本文件,并将其命名为指定的名称。如果你想在文件中添加内容,可以使用以下命令:
这将在文件中添加指定的文本。如果文件不存在,则将创建一个新文件。如果文件已经存在,则将覆盖其内容。
二、批量更改后缀名
修改
法①:
您可以使用以下命令将指定目录及其子目录下的所有文件的后缀名都更改为指定的新后缀名:
其中,将 “目录路径” 替换为您需要批量更改后缀名的文件所在的目录的绝对路径,然后将“新后缀名”替换成您想要修改的新后缀名。该命令将修改指定目录及其子目录下所有文件的后缀名为新后缀名。
例如,如果您想将D盘根目录下的所有文件后缀名改为“.txt”,则可以使用以下命令:
当命令执行完毕后,您就可以找到您要批量改名后缀名的所有文件都已经被改名为新后缀名了。
注意:如果您将该命令保存为批处理文件(批处理文件的后缀名通常为.bat),则将“%i”改为“%%i”。
法②:
- 打开记事本,输入以下命令,并保存为“change_ext.bat”文件:
- 双击运行“change_ext.bat”文件,在命令提示符中输入以下命令:
-
上面的命令中,
C:\test是指定目录路径,.txt是需要改变的后缀名,可以根据需要进行修改。 -
如果需要排除
change_ext.bat这个文件,可以将命令修改为:
- 保存文件后,输入上述命令即可在指定目录内批量改变后缀名,且不改变这个
.bat文件。
还原
如果目录下的原始文件后缀名不一样,您可以通过以下命令来批量还原:
将代码复制到记事本中,把 D:\docs 改为您想要操作的目录路径,保存为批处理文件(后缀名为 .bat),然后双击运行即可。
该脚本通过查询目录下的每个文件的完整路径,来针对每个文件进行后缀名替换。这样即使同一个目录下的文件的原始后缀名不一致,也可以正确还原文件的后缀名到原始状态。
但请注意,批处理还原所有文件的后缀名可能会有一定风险,请确保已经备份了重要的文件并仔细检查了新旧文件后缀名的对应,以免数据丢失。
三、VS Code 插件 Markdown All in One
Markdown All in One是一款VS Code插件,可以方便快捷地编写和预览Markdown文件。使用步骤如下:
-
安装插件
在VS Code中按Ctrl+Shift+X或者点击左侧的扩展按钮,搜索“Markdown All in One”,安装插件。 -
编写Markdown文件
在新建文件时选择Markdown格式,然后开始编写Markdown文本。 -
使用快捷键
Markdown All in One提供了丰富的快捷键,如:
Ctrl+B或Cmd+B:插入粗体文本Ctrl+I或Cmd+I:插入斜体文本Ctrl+L或Cmd+L:插入链接Ctrl+Shift+K或Cmd+Shift+K:插入行内代码Ctrl+Shift+V或Cmd+Shift+V:预览文档
- 预览Markdown文件
在编辑Markdown文本时,按下Ctrl+Shift+V或Cmd+Shift+V,即可在预览窗口中查看Markdown的渲染效果。同时,你可以在预览窗口中进行滚动和查找操作,实时查看Markdown文本的排版效果。
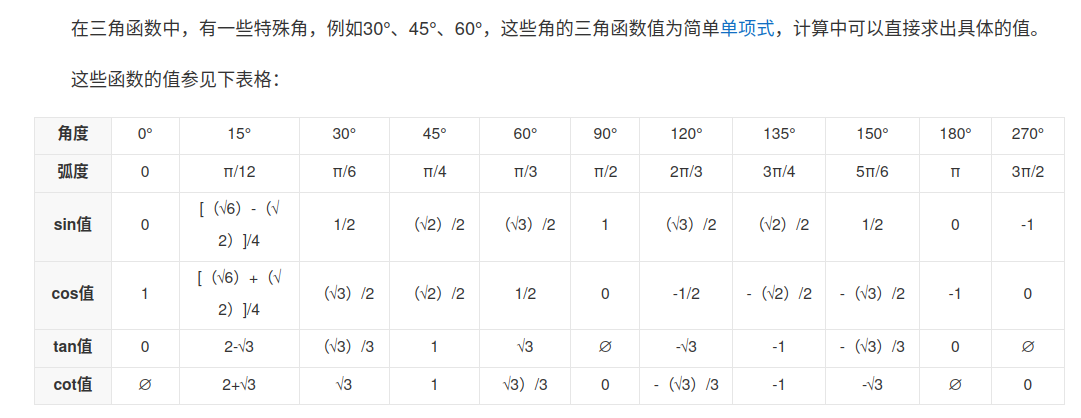
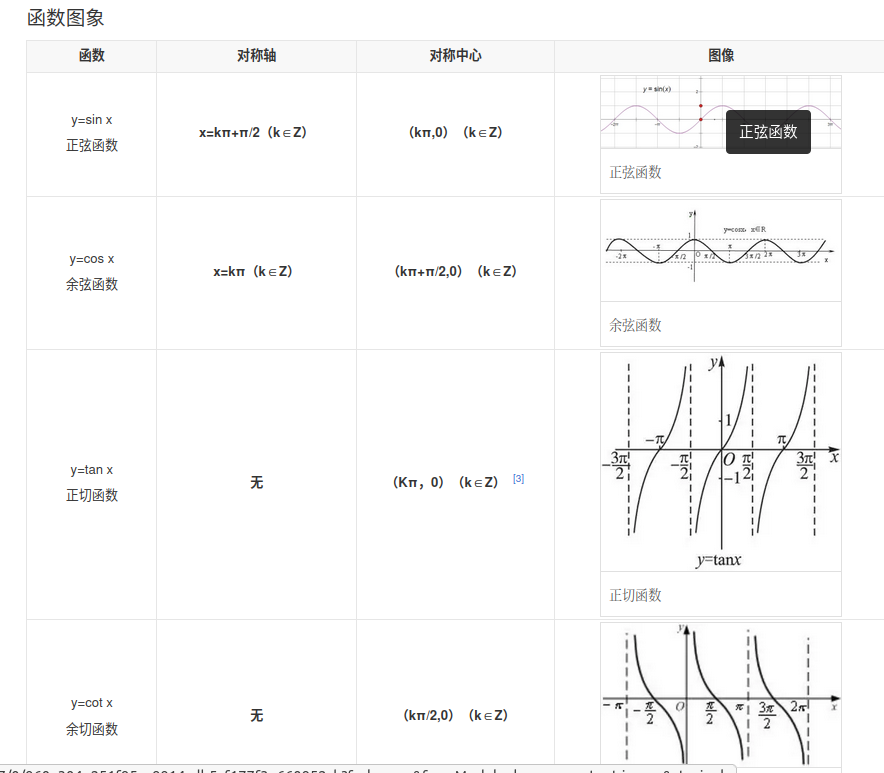
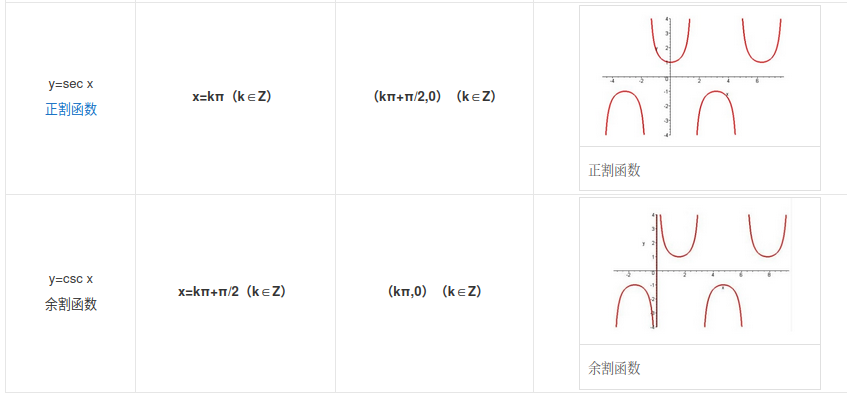
四、数学
三角函数
极限
重要极限
导数
符号定义:
定义:说的简单一点,就相当于运动学中的瞬时速度,即曲线的切线。
导数形式 :对于任意函数
它与
当然也可以写成
常用求导公式
一些求导公式的证明
- (10)
由题且根据定义式可得
即
推到这里,就需要证明:
显然
则设
在设
所以
所以
得
函数求导法则(加减乘除)
反函数求导
复合函数求导
结语
__EOF__
本文链接:https://www.cnblogs.com/GOD-HJ/p/17625492.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!















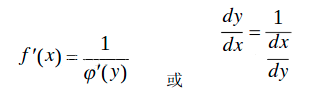
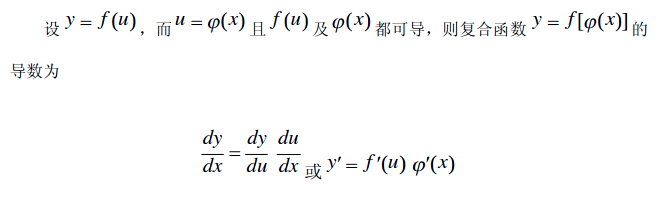


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本