2023年多校联训NOIP层测试1
闲来无事,补个博客。题目全是COCI的原题
T1 打字(\(50pts\))
题目
思路
字符串处理,注意所有情况如: B 是一个名字,B1 不是。
code
#include<bits/stdc++.h>
using namespace std;
int sum,o,m,ans[10010],cnt=1;
char s[10010];
signed main(void){
scanf("%d",&o);
while(scanf("%s",s+1)!=EOF){
//cout<<(s+1)<<endl;
int n=strlen(s+1);
int f=(s[1]>='A'&&s[1]<='Z');
if(f) for(int i=2;i<n;++i) if(!(s[i]>='a'&&s[i]<='z')) f=0;//是否有不是数字的
if((s[n]=='.'||s[n]=='?'||s[n]=='!')){
printf("%d\n",sum+f);
sum=0;
}
else if(f&&((s[n]>='a'&&s[n]<='z')||(n==1))) ++sum;
}
return 0;
}
T2 下棋(\(6pts\))
COCI原题:pohlepko
题目

思路
\(50pts\)
贪心
因为数据规定每个格子右边和下边的两个英文字母不同,依次选择字典序最小的字母即可。
\(70pts\)
搜索
\(100pts\)
枚举
对于每一步,步数相同时,坐标 \((x,y)\),\(x+y\) 的值相同。所以基本思路是:
枚举每一步中的所有字母,同时需要判断上一步是否可到达(才能走到当前位置),选出其中字典序最小的,标记这些位置是可达
的,这些位置可以进行扩展。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e3+10;
int y,n,m;
char a[N][N];
bool vis[N][N];
signed main(void){
scanf("%d%d",&n,&m);
memset(a,'z',sizeof a);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
cin>>a[i][j];
}
}
cout<<a[1][1];
vis[1][1]=1;
for(int i=2;i<=n+m-1;++i){
char o='z';
for(int j=1;j<=n;++j){
y=i-j+1;
if(y>=1&&y<=m){
if(vis[j-1][y]&&a[j][y]<o) o=a[j][y];
if(vis[j][y-1]&&a[j][y]<o) o=a[j][y];
}
}
cout<<o;
for(int j=1;j<=n;++j){
y=i-j+1;
if(y>=1&&y<=m){
if(vis[j-1][y]&&a[j][y]==o) vis[j][y]=1;
if(vis[j][y-1]&&a[j][y]==o) vis[j][y]=1;
}
}
}
return 0;
}
T3 分钱(\(0pts\))
题目

思路

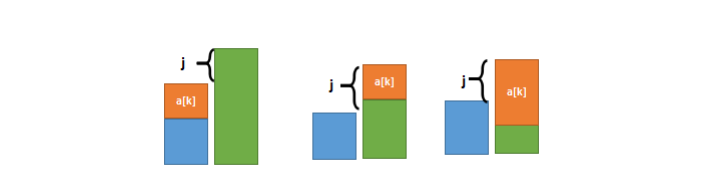
code
#include<bits/stdc++.h>
using namespace std;
int n,a[550],dp[550][100001],sum;
signed main(void){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",a+i);
sum=sum+a[i];
}
memset(dp,-0x3f,sizeof dp);
dp[0][0]=0;
for(int i=1;i<=n;++i){
for(int j=0;j<=sum;++j){
dp[i][j]=dp[i-1][j];
dp[i][j]=max(dp[i][j],dp[i-1][abs(j-a[i])]+a[i]);
dp[i][j]=max(dp[i][j],dp[i-1][j+a[i]]+a[i]);
}
}
printf("%d\n",sum-dp[n][0]/2);
return 0;
}
T4 超级英雄(\(0pts\))
题目

思路
(闲话:因为出题人直接把他原题的英文全部扔进了百度翻译,把 左右相邻或上下相邻,即四连通 翻译成了 并排相邻。让我喜提此题爆 \(0\)。)

在luogu过得在accoders上被卡的代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
const int dx[]={0,1,0,-1};
const int dy[]={1,0,-1,0};
int qqqq,n,m,k;
struct node{int x,y;};
bool vis[41],pd[N][N];
int co[N][N],kkkkk,dis[41][N][N];
vector<node>qq[41];
queue<node>q;
inline void bfs(int o){
memset(vis,0,sizeof vis);
memset(pd,0,sizeof pd);
for(node i:qq[o]){
int x=i.x,y=i.y;
dis[o][x][y]=0;
q.push(i);
pd[x][y]=1;
}
vis[o]=1;
while(!q.empty()){
int x=q.front().x,y=q.front().y,w=co[x][y],u=dis[o][x][y];
q.pop();
if(!vis[w]){
vis[w]=1;
for(node i:qq[w]){
int xx=i.x,yy=i.y;
if(!pd[xx][yy]){
dis[o][xx][yy]=u+1;
q.push(node{xx,yy});
pd[xx][yy]=1;
}
}
}
for(int i=0;i<4;++i){
int xx=x+dx[i],yy=y+dy[i];
if(xx>0&&xx<=n&&yy>0&&yy<=m&&!pd[xx][yy]){
q.push(node{xx,yy});
dis[o][xx][yy]=u+1;
pd[xx][yy]=1;
}
}
}
return ;
}
signed main(void){
//mt19937 rnd(random_device{}());
//memset(dis,-1,sizeof dis);
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf("%d",&co[i][j]);
qq[co[i][j]].push_back((node){i,j});
// if(i==1&&j==1) kkkkk=co[i][j];
// if(kkkkk!=co[i][j]) kkkkk=-1;
}
}
for(int i=1;i<=k;++i){
bfs(i);
}
scanf("%d",&qqqq);
for(int ans,r1,c1,r2,c2,i=1;i<=qqqq;++i){
scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
ans=abs(r1-r2)+abs(c1-c2);
// if(r1==r2&&c1==c2){printf("0\n");continue;}
// else if(kkkkk!=-1){printf("1\n");continue;}
// else if(co[r1][c1]==co[r2][c2]){printf("1\n");continue;}
for(int i=1;i<=k;++i){
ans=min(ans,dis[i][r1][c1]+dis[i][r2][c2]+1);
}
printf("%d\n",ans);
}
return 0;
}
卡常后的代码
点击查看代码
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
using namespace std;
inline int Min(int x,int y){return x<y? x:y;}
inline int Abs(int x){return x<0? -x:x;}
inline int read(){
int x=0;
bool f=true;
char s=getchar();
for(;s<'0'||s>'9';s=getchar()) if(s=='-') f=false;
for(;'0'<=s&&s<='9';s=getchar()) x=(x<<1)+(x<<3)+(s^48);
return f? x:-x;
}
#define read read()
void write(int x){
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+48);
}
int n,m,k,a[1010][1010],color[50];
vector<int> x[50],y[50];
int dist[50][1010][1010],dx[]={-1,0,1,0},dy[]={0,1,0,-1};
struct myqueue{
int q[1000000];
int l=1,r=1;
inline void push(int x){
q[++r]=x;
}
inline int front(){
return q[l+1];
}
inline void pop(){
l++;
}
inline int back(){
return q[r];
}
inline bool empty(){
return r<=l;
}
};
signed main(){
n=read,m=read,k=read;
int i,j,c;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
a[i][j]=read;
++color[a[i][j]];
x[a[i][j]].push_back(i);
y[a[i][j]].push_back(j);
}
}
for(c=1;c<=k;++c){
myqueue qx,qy;
bool vis[41]={false};
vis[c]=true;
for(i=0;i<color[c];++i){
qx.push(x[c][i]);
qy.push(y[c][i]);
dist[c][qx.back()][qy.back()]=1;
}
while(!qx.empty()){
int i=qx.front(),j=qy.front();
qx.pop();qy.pop();
for(register int l=0;l<4;++l){
int nx=i+dx[l],ny=j+dy[l];
if(1>nx||nx>n||1>ny||ny>m) continue;
if(!dist[c][nx][ny]){
qx.push(nx);
qy.push(ny);
dist[c][qx.back()][qy.back()]=dist[c][i][j]+1;
}
}
if(!vis[a[i][j]]){
int colour=a[i][j];
vis[colour]=true;
for(register int l=0;l<color[colour];++l){
if(!dist[c][x[colour][l]][y[colour][l]]){
qx.push(x[colour][l]);
qy.push(y[colour][l]);
dist[c][x[colour][l]][y[colour][l]]=dist[c][i][j]+1;
}
}
}
}
}
int Q=read,ans;
while(Q--){
int x1=read,y1=read,x2=read,y2=read;
ans=Abs(x1-x2)+Abs(y1-y2);
for(register int i=1;i<=k;++i){
ans=Min(ans,dist[i][x1][y1]+dist[i][x2][y2]-1);
}
write(ans);
putchar('\n');
}
}