数据结构 - 从二叉搜索树说到AVL树（一）之二叉搜索树的操作与详解（Java）

　　二叉搜索树（Binary Search Tree），简称BST，顾名思义，一颗可以用于搜索的二叉树。BST在数据结构中占有很重要的地位，一些高级树结构都是其的变种，例如AVL树、红黑树等，因此理解BST对于后续树结构的学习有很好的作用。同时利用BST可以进行排序，称为二叉排序，也是很重要的一种思想。

　　二叉树的性质：任意一个节点的所有左子树元素都比该元素值要小，而所有右子树元素都比该元素值要大。

　　符合该性质的二叉树就是一颗二叉搜索树，当然前提下是树中不允许有重复元素。

　　所有的二叉搜索树的中序遍历序列都是一个顺序序列， 以下的几种都是二叉搜索树

　　

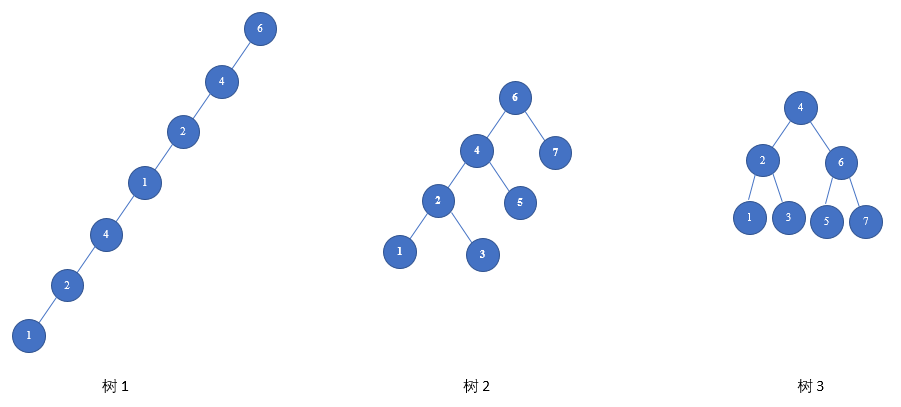
　　接下来讲二叉搜索树的三个主要操作：查找，增加，删除。

　　一、查找

　　　　二叉搜索树本来就是用于查找数据的一种结构，主要步骤是：

　　　　　　① 选择根节点作为当前节点

　　　　　　② 如果当前节点为null，则返回false表示找不到该元素

　　　　　　③ 如果当前节点不为null，判断当前节点是否与所搜索元素相等，如相等，则返回true表示能找到该元素

　　　　　　④ 如果当前节点的值比所搜索值小，则选择当前节点的左节点作为当前节点，比搜索值大则选择右节点作为当前节点，然后从②循环过程

　　二、增加

　　　　二叉搜索树增加节点重点是根据查找元素的过程找到该节点的插入位置：

　　　　　　① 如果根节点为空，则当前插入（增加）的节点为二叉树的根，如根节点不为空，设置根节点为当前节点

　　　　　　② 如果当前节点的值与插入节点的值相等，返回false表示插入失败，节点值已存在于树中

　　　　　　③ 若插入节点的值比当前节点的值小，且当前节点的左子树为空，则把插入节点增加到当前节点的左子树，并返回true表示插入成功，如左子树不为空，设置当前节点的左子树为当前节点。

　　　　　　　 如果插入节点的值比当前节点的值大，且当前节点的右子树为空，则把插入节点增加到当前节点的右子树，并返回true，如右子树不为空，设置当前节点的右子树为当前节点。

　　　　　　　 从②循环过程

　　　　具体代码如下：

    public boolean insert(int elem) {
        TreeNode node = new TreeNode(elem);
        if (null == this.root) {
            this.root = node;
            return true;
        } else {
            return insertChild(this.root, node);
        }
    }    
    /**
     * insert the newNode to the child position of parent node
     * @param parent
     * @param newNode
     * @return true if the newNode insert successfully or false if the newNode have been exist
     */
    private boolean insertChild(TreeNode parent, TreeNode newNode) {
        if (parent.getElem() == newNode.getElem()) {
            return false;
        } else if (parent.getElem() > newNode.getElem()) {
            if (null  == parent.getLeft()) {
               parent.setLeft(newNode);
               newNode.setParent(parent);
               return true;
            } else {
               return insertChild(parent.getLeft(), newNode);
            }
        } else {
            if (null == parent.getRight()) {
               parent.setRight(newNode);
               newNode.setParent(parent);
               return true;
            } else {
               return insertChild(parent.getRight(), newNode);
            }
        }
    }

　　三、删除

　　　　二叉搜索树的删除操作重点在于删除这个节点之后对其他节点的重组，根据删除节点位置又分为以下几种情况：

　　　　　　情况1 删除节点为叶子节点：直接删除这个节点（把父节点对应的子树设为空）

　　　　　　情况2 删除节点只有左子树或只有右子树：用左子树或者右子树代替被删除节点（把父节点对应的子树指向删除节点的左子树或者右子树，并把左子树或右子树的父节点指向删除节点的父节点）

　　　　　　*情况3 删除节点的左子树和右子树均不为空：找到删除节点的直接前驱节点，用该前驱节点的值替换待删除节点的值，然后把这个前驱节点当做待删除节点，则该情况转换成情况1或者情况2

　　　　　　比如想删除节点 4

　　　　

 

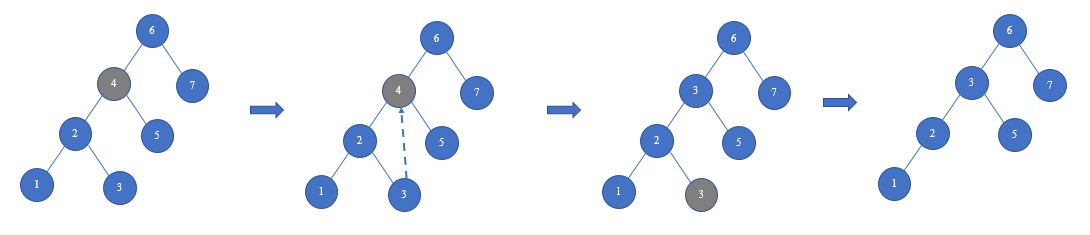
 　　　　　找到节点4的直接前驱节点3，用节点3的值代替节点4的值，然后情况换成删除节点3（也就是情况1）。

　　　　具体代码：

    /**
     * delete the node which element equals to parameter elem
     * @param elem
     * @return true if the node can be found and delete otherwise false
     */
    public boolean delete(int elem) {
        if (null == this.root) {
            return false;
        } else {
            TreeNode node = this.root;
            // find out the node need to be deleted
            while (null != node) {
                if (node.getElem() == elem) {
                    deleteNode(node);
                    return true;
                } else if (node.getElem() > elem) {
                    node = node.getLeft();
                } else {
                    node = node.getRight();
                }
            }
            return false;
        }
    }
    private void deleteNode(TreeNode node) {
        if (null == node.getLeft() && null == node.getRight()) {
            // deleted node is a leave
            if (null  == node.getParent()) {
                // deleted node is root
                this.root = null;
            } else if (node == node.getParent().getLeft()) {
                // deleted node is the left child of its parent
                node.getParent().setLeft(null);
            } else {
                // deleted node is the right child of its parent
                node.getParent().setRight(null);
            }
        } else if (null == node.getLeft()) {
            // deleted node only hae right child
            if (null  == node.getParent()) {
                this.root = node.getRight();
            } else if (node == node.getParent().getLeft()) {
                node.getParent().setLeft(node.getRight());
            } else {
                node.getParent().setRight(node.getRight());
            }
            node.getRight().setParent(node.getParent());
        } else if (null == node.getRight()) {
            // deleted node only have left child
            if (null  == node.getParent()) {
                this.root = node.getLeft();
            } else if (node == node.getParent().getLeft()) {
                node.getParent().setLeft(node.getLeft());
            } else {
                node.getParent().setRight(node.getLeft());
            }
            node.getLeft().setParent(node.getParent());
        } else {
            // deleted node have both left & right children
            // find out the precursor of deleted node
            // the precursor node replace the position of deleted node
            TreeNode pre = node.getLeft();
            while (null != pre.getRight()) {
                pre  = pre.getRight();
            }
            // swap the elem of precursor node and deleted node
            // then delete the precursor node
            TreeUtils.swapTreeElem(pre, node);
            deleteNode(pre);
        }
    }

写个小程序测试一下：

输入测试数据：10 5 2 7 6 18 13 -1（-1是结束输入，不作为一个元素值）

1. insert
2. delete
3. search
4. print
5. exit
->1
->10 5 2 7 6 18 13 -1
insert success

看一下树的结构，显示树结构的需要顺时针转90°来看，并自己想象节点连线。。

1. insert
2. delete
3. search
4. print
5. exit
->4
-
    18
        13
10
        7
            6
    5
        2
-

删除节点 5 测试效果

1. insert
2. delete
3. search
4. print
5. exit
->2
->5
delete success
--------------------------------------------------------------
1. insert
2. delete
3. search
4. print
5. exit
->4
-
    18
        13
10
        7
            6
    2
-

 至此， 二叉搜索树的操作及具体实现完成，如有不妥之处，欢迎指出斧正。

 

 

尊重知识产权，转载请标明出处并通知作者。