根据 中序遍历 和 后序遍历构造树（Presentation）（C++）

　　好不容易又到周五了，周末终于可以休息休息了。写这一篇随笔只是心血来潮，下午问了一位朋友PAT考的如何，顺便看一下他考的试题，里面有最后一道题，是关于给出中序遍历和后序遍历然后求一个层次遍历。等等，我找一下链接出来......

　　1127. ZigZagging on a Tree (30)：https://www.patest.cn/contests/pat-a-practise/1127

　　突然想起以前学数据结构的时候如果给出一个中序遍历和一个后序遍历然后让你画出树的结构或求出先序遍历之类的题目，如果用笔来画，三下五除二能够一下子就画出来，但关于用语言编写出来却从来没有想过，真是惭愧，所以这篇随笔的内容思维可能比较简单低阶，请大家包涵。

　　所以想试一下能不能写一写，加之最近在补习一些算法和数据结构之类的题目，可以作为一个练手的题目。想不到要动手之前理清一下构造的过程，最后却有些明朗的感觉，这也是我想写下这篇随笔的原因，虽然简单，但很有意义。好，说了这么多废话...下面开始：

　　对于一棵树的中序遍历，根节点肯定处于遍历结果的中间（假设这棵树有左子树），后序遍历的时候根节点肯定是最后一个遍历的元素。所以可以轻易得到根在中序遍历中的位置，根据中序遍历的性质，以根为中点往后遍历到的元素就是这棵树的右子树元素，往前遍历到的就是这棵树的左子树元素。而后续遍历也是把这棵树的左子树全部遍历完整之后再来遍历右子树，因此在后续遍历中，左子树和右子树的元素也是有明显的界限。而对于根节点的左节点和右节点也是同样的道理。举个例子

                  

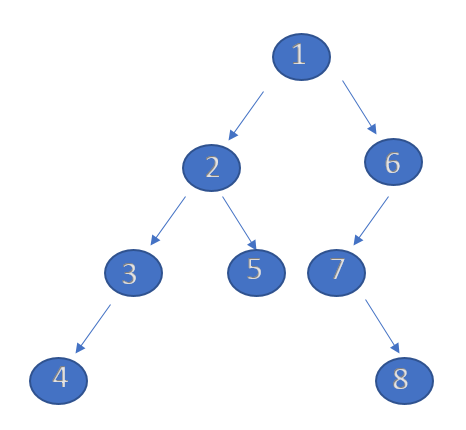
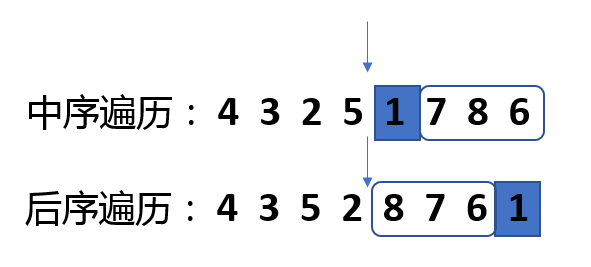
所以我们从最初的遍历顺序开始，找出后续遍历的最后一个元素在中序遍历中的位置，然后以这个位置为重点，往右的遍历元素为A,往左的遍历元素为B，根据A和B的长度可以确定在后续遍历中的遍历元素边界，对A和B进行上一步的操作，直到所有元素遍历完成。代码：

Node *getRoot(int* inorder,int* postorder,int ix,int iy,int px,int py){
    Node *node = new Node(postorder[py]);
    int p = findElem(inorder,postorder[py],ix,iy);
    if(-1 != p){
        int lix,liy,lpx,lpy,rix,riy,rpx,rpy;
        if(p == iy)node->right = NULL;
        else{
            rix = p+1;
            riy= iy;
            rpy = py-1;
            rpx = rpy - (riy-rix);
            node->right = getRoot(inorder,postorder,rix,riy,rpx,rpy);
        }
        if(p == ix) node->left = NULL;
        else{
            lix = ix;
            liy = p -1;
            lpx = px;
            lpy = px + (liy-lix);
            node->left = getRoot(inorder,postorder,lix,liy,lpx,lpy);
        }

        return node;
    }else
    return NULL;
}
void MidTraverse(Node *root){
    if(NULL != root){
        cout<<root->val<<" ";
        MidTraverse(root->left);
        MidTraverse(root->right);
    }
}
int main(){
    int count;
    cin>>count;
    int *inorder = new int[count];
    int *postorder = new int[count];
    for(int i =0;i<2;i++){
        for(int j=0;j<count;j++){
            int in;
            cin>>in;
            if(0==i) inorder[j] = in;
            else postorder[j] = in;
        }
    }
    Node *root = getRoot(inorder,postorder,0,count-1,0,count-1);
    if(NULL !=root)
        MidTraverse(root);
}

节点定义为：

typedef struct _Node{
    int val;
    struct _Node *left,*right;
    _Node(int _val):val(_val),left(NULL),right(NULL){}
}Node;

运行代码，最后结果在意料之内：

 

 

 

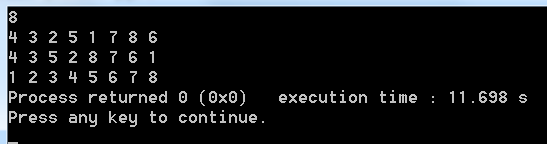
        深圳的工作压力强行把市民的生活节奏拉的飞快，上了一周的班心绪有些烦躁，下班出了公司的门却意外地迎来了树叶和泥土的味道，是一场雨清澈了整片空气。