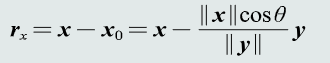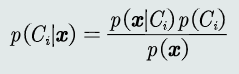《机器学习》第一次作业——第一至三章学习记录和心得
第一章 模式识别基本概念
1.1 什么是模式识别
- 模式识别的定义:根据已有知识的表达或者说是函数映射,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值,是一种推理过程,可划分为“分类”和“回归”两种形式。
- 分类:输出量是离散的类别表达,即输出待识别模式所属的类别——二类/多类分类
- 回归:回归是分类的基础——离散的类别值是由回归值做判别决策得到的。输出量是连续的信号表达(回归值);输出量维度:单个/多个维度
1.2 模式识别数学表达
- 模式识别数学解释:可以看做一种函数映射f(x),将待识别模式x从输入空间映射到输出空间。函数f(x)是关于已有知识的表达。
- 输入空间:原始输入数据x所在的空间
- 输出空间:输出的类别/回归值y所在的空间
- 模型:已有知识的表达方式,即f(x)
- 模型可用于回归和分类
- 判别函数:特定的非线性函数,记作函数g。通常已知,不作为模型组成
- 二类分类:sign函数
- 多类分类:max函数(去最大的回归值所在维度对应类别)
- 特征的特性:1.具有辨别能力:提升不同类别之间的识别性能,基于统计学规律而非个例;2.具有鲁棒性:针对不同的观测条件,仍能够有效表达类别之间的差异性
- 特征向量的定义和性质:

1.3 特征向量的相关性
- 点积的代数定义:点积的结果是一个标量表达;点积具备对称性;点积是一个线性变换
- 点积的几何定义:点积可以表征两个特征向量的共线性,即方向上的相似程度。点积=0,说明两个向量是正交的
- 残差向量:向量x分解到向量y方向上得到的投影向量原向量x的误差
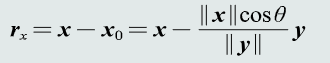
- 欧氏距离:表征两个向量之间的相似程度(综合考虑方向和模长)
1.4 机器学习基本概念
- 线性模型:模型结构是线性的(直线、面、超平面):y=(W^T)x+W0(w,w0是模型参数)
- 非线性模型:模型结构非线性,y=g(x)。常见非线性模型:多项式、神经网络、决策树
- 样本量与模型参数量的关系:N=M:参数有唯一解;N>>M:没有准确的解;N<<M:无数个解/无解
- 目标函数:对于over-determined的情况,需要额外添加一个标准,通过优化该标准来确定一个近似解,这个标准就是目标函数,也叫代价函数或损失函数
- 机器学习方式:真值(标签)&标注;监督式学习:训练样本及输出真值都给定情况下的机器学习;无监督式学习:只给定训练样本,没有给输出真值情况下的机器学习算法;半监督式学习:既有标注的训练样本,又有未标注的训练样本情况下的学习算法
- 强化学习:机器自行探索决策、真值滞后反馈的过程
1.5 模型的泛化能力
- 泛化能力:即训练得到的模型不仅要对训练样本有决策能力,也要对新的模式具有决策能力。
- 过拟合:泛化能力低的表现。模型训练阶段表现很好,但在测试阶段表现很差。模型过于拟合训练数据
- 提高泛化能力:选择复杂的模型;正则化:在目标函数中加入关于参数的正则项,通过调节正则系数,降低过拟合的程度
1.6 评估方法与性能指标
- 随机划分:训练集和测试集,用训练集训练模型,用测试集评估模型量化指标;取统计值:取量化指标的平均值/方差/最大值等作为最终性能量化评估结果
- K折交叉验证:将数据集分割成K个子集,从中选取单个子集作为测试集,其余作为训练集;交叉验证重复K次,使每个子集被测试一次;K次评估值取平均作为最终量化评估结果
- 留一验证:每次只取数据集中一个样本做测试集,其余做训练集;每次样本测一次,取所有评估值的平均值作为最终评估结果;等同于K折交叉验证,K为数据集样本总数
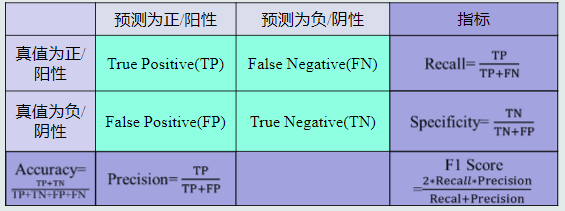
- 性能指标
第二章 基于距离的分类器
2.1 MED分类器
- 基于距离的决策:初级的模式识别技术,是其他识别决策技术的基础
- 定义:把测试样本到每个类之间的距离作为决策模型,将测试样本判定为与其距离最近的类
- 类的原型:用来代表这个类的一个模式或者一组量,便于计算该类和则是样本之间的距离
- 距离度量标准
非负性:d(x,z) >= 0
对称性:d(x,z) = d(z,x)
三角不等式:d(x,z) <= d(x,y) + d(y,z)
- 常见的几种距离度量

- MED分类器的概念:最小欧式距离分类器
- MED分类器的决策边界方程

2.2 特征白化
- 目的:将原始特征映射到一个新的特征空间,使得在新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性
- 步骤:1.去除特征之间的相关性——解耦:通过W1实现协方差矩阵对角化;2.对特征进行尺度变换——白化:通过W2对上一步变化后的特征再进行尺度变换,实现所有特征具有相同方差。
2.3 MICD分类器
- 概念:最小类内距离分类器,基于马氏距离,经过特征正交白化,去除特征变化的不同及特征之间的相关性,缺陷是会选择方差较大的类。
第三章 贝叶斯决策与学习
3.1 贝叶斯决策与MAP分类器
- 后验概率:给定一个测试模式x,决策其属于哪个类别需要依赖于P(Ci|x),该表达式称为后验概率,表达给定模式x属于类Ci的可能性。
- 贝叶斯规则:已知先验概率和观测概率,模式𝒙属于类𝐶𝑖后验概率的计算公式为:
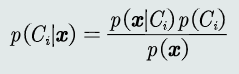
- MAP分类器:将测试样本决策分类给后验概率最大的那个类。给定所有测试样本, MAP分类器选择后验概率最大的类,等于最小化平均概率误差,即最小化决策误差。
3.2 MAP分类器:高斯观测概率
- 先验和观测概率表达方式:1.常数表达:P(Ci)= 0.2;2.参数化解析表达:高斯分布……;3.非参数化表达:直方图、核密度、蒙特卡洛……
- MAP分类器会倾向于选择先验概率大,分布紧致的类,解决了MED和MICD的问题
3.3 决策风险与贝叶斯分类器
- 损失:表征当前决策动作相对于其他候选类别的风险程度,记为λ(αi|Cj),简写为λij
- 贝叶斯分类器:在MAP分类器基础上,加入决策风险因素,得到贝叶斯分类器,给定一个测试样本𝒙,贝叶斯分类器选择决策风险最小的类。给定所有测试样本 {𝒙},贝叶斯分类器的决策目标: 最小化期望损失。
- 朴素贝叶斯分类器:如果特征是多维的,则特征之间的相关性会导致学习困难。通过假设特征之间是相互独立(即独立同分布),进而简化计算,此为朴素贝叶斯
3.4 最大似然估计
- 参数化方法:给定概率分布的解析表达,学习这些解析表达中的参数,又称参数估计
- 最大似然估计

3.5 最大似然的估计偏差
- 无偏估计:如果一个参数的估计量的数学期望是该参数的真值,则该估计量称作无偏估计,意味着只要训练样本个数足够多,该估计值就是参数的真实值
- 高斯分布均值的最大似然估计是无偏估计;高斯分布协方差的最大似然估计是有偏估计
3.6 贝叶斯估计
- 贝叶斯估计:给定参数𝜃分布的先验概率以及训练样本,估计参数θ分布的后验概率
- 贝叶斯估计具备不断学习的能力。允许最初不太准确的估计,随着训练样本的不断增加而修正估计值,从而达到期望真值
- 贝叶斯估计流程步骤

3.7 KNN估计
- 若概率分布形式未知,可通过无参数技术实现概率密度估计。常用五参数技术:KNN、直方图、核密度估计
- KNN估计:给定𝒙,找到其对应的区域𝑅使其包含𝑘个训练样本,以此计算𝑝(𝒙)
- KNN估计的优缺点:可以自适应的确定𝒙相关的区域𝑅的范围,但不是真正的概率密度表达,概率密度函数积分是 ∞ 而不是1
3.8 直方图与核密度估计
- KNN估计的问题:在推理测试阶段仍需存储所有训练样本。对任意模式x,需要以其为中心,在训练样本中选k个相邻点估计该模式的概率;区域R是由第k个相邻点确定的,易受噪声影响
- 直方图估计:直接将特征空间划分为m个格子(bins),每个格子是一个区域R,位置固定、大小固定,相邻格子不重叠,k值不需要给定
- 核密度估计:以𝒙为中心固定带宽h,计算落入R的样本个数,以此计算𝑝(𝒙)。
- 核密度估计的优缺点:可以自适应确定R的代销,克服了KNN估计存在的噪声影响。但是要储存所有训练样本,耗费空间大。
- 带宽选取的原则:泛化能力。因为给定训练样本数量是有限的,故要求根据训练样本估计出的概率分布既能符合训练样本,同时也要有一定预测能力,即能估计未看见的模式