Luogu6628 [省选联考 2020 B 卷] 丁香之路

Luogu6628 [省选联考 2020 B 卷] 丁香之路

\(Kruskal\)+欧拉回路

这道题相当妙啊。

本题钦定了起点和终点，容易发现满足题意的路径是一条欧拉路径。欧拉路径的性质是奇点个数为\(0\)或\(2\)，在本题中\(s\)和\(i\)恰好是两个奇点，因此剩下的路径上的点的度数应当为偶数。

把起点\(s\)度数和终点\(i\)度数\(+1\)，并连接\(s,i\)，就转化成了求解欧拉回路（这样实际上\(s\)和\(i\)就是两个奇点了，而其他点均为偶点，可以理解为：去掉我们自己添加的边\(s-i\)后，我们即可获得欧拉路径）。

我们可以把奇点找出来，由于图中点\(i,j\)路径长度为\(\lvert i-j \rvert\)，两点间直接路径最短，我们可以贪心地将相邻的奇点配对连边，使之成为偶点，一条边贡献的度数是\(2\)，总度数为偶数，这样的方案一定存在。

但是会出现一个问题，可能我们最终得到的是很多欧拉回路，它们并不连通。

我们可以建立最小生成树将他们连通，边权需要\(\times 2\)，因为我们总体需要形成欧拉回路。

为了使得更多的点连通，我们把边全部拆成边权为\(1\)的边，也就是\(u-v(u<v)\)变为\(u-(u+1)- \cdots -(v-1)-v\)。

建立最小生成树的过程会仍会导致新的连边，这会不会使答案变劣呢？

由于边权为\(1\)，已经无法拆分边了，我们可以考虑是否存在其他更优方案。

比如有四个节点\(A<B<C<D\)（其他中间路程中的点被省略）。

我们的算法会这样连：

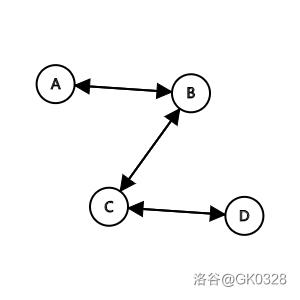
边权和为：\(2(B-A)+2(D-C)+2(C-B)=2D-2A\)。

很容易怀疑以下方式是否更优：

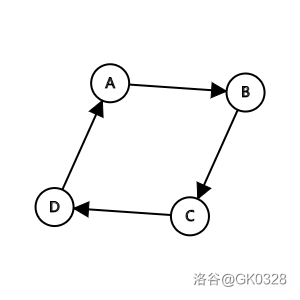
边权和为：\((B-A)+(C-B)+(D-C)+(D-A)=2D-2A\)。

发现我们的计算方式不会让答案变劣。

因此我们证明了这是最优选取方式。

\(Code:\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#define N 2505
using namespace std;
int n,m,s,x,y;
int res=0,ans=0;
int fa[N],f[N];
int d[N];
bool vis[N];
int getf(int x)
{
    return (fa[x]==x)?x:(fa[x]=getf(fa[x]));
}
struct edge
{
    int x,y,z;
    edge (int xx=0,int yy=0,int zz=0)
    {
        x=xx,y=yy,z=zz;
    }
    bool operator < (const edge &A) const
    {
        return z<A.z;
    }
};
vector<edge>e;
int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for (int i=1;i<=n;++i)
        fa[i]=i;
    for (int i=1;i<=m;++i)
    {
        scanf("%d%d",&x,&y);
        ++d[x],++d[y];
        vis[x]=vis[y]=true;
        res+=abs(x-y);
        fa[getf(x)]=getf(y);
    }
    for (int i=1;i<=n;++i)
        f[i]=getf(i);
    vis[s]=true;
    for (int i=1;i<=n;++i)
    {
        ans=res;
        memcpy(fa+1,f+1,n*sizeof(int));
        ++d[s],++d[i];
        fa[getf(s)]=getf(i);
        bool t=vis[i];
        vis[i]=true;
        int pre=-1;
        for (int j=1;j<=n;++j)
            if (d[j] & 1)
            {
                if (~pre)
                {
                    ans+=j-pre;
                    for (int k=pre;k<j;++k)
                        fa[getf(k)]=getf(j);
                    pre=-1;
                } else
                    pre=j;
            }
        e.clear();
        pre=-1;
        for (int j=1;j<=n;++j)
            if (vis[j])
            {
                if (~pre && getf(j)!=getf(pre))
                    e.push_back(edge(getf(j),getf(pre),j-pre));
                pre=j;
            }
        sort(e.begin(),e.end());
        for (vector<edge> :: iterator it=e.begin();it!=e.end();++it)
        {
            int fx=getf(it->x),fy=getf(it->y);
            if (fx==fy)
                continue;
            ans+=it->z << 1;
            fa[fx]=fy;
        }
        printf("%d ",ans);
        --d[s],--d[i];
        vis[i]=t;
    }
    putchar('\n');
    return 0;
}