Luogu4565 [CTSC2018]暴力写挂
Luogu4565 [CTSC2018]暴力写挂
边分治
边分治与点分治相似,每次选择断开后得到的两棵子树大小的最大值最小的边,可以与点分治寻找重心类比。
但是对于一般树来说,它并不一定有一条边具有使断边后最大子树大小呈指数级下降的特质(比如\(n-1\)个点连向\(1\)个点)。
我们可以利用虚点,将一棵树变为二叉树,具体来说,有两种方式。
对于以下的树:

方案一:
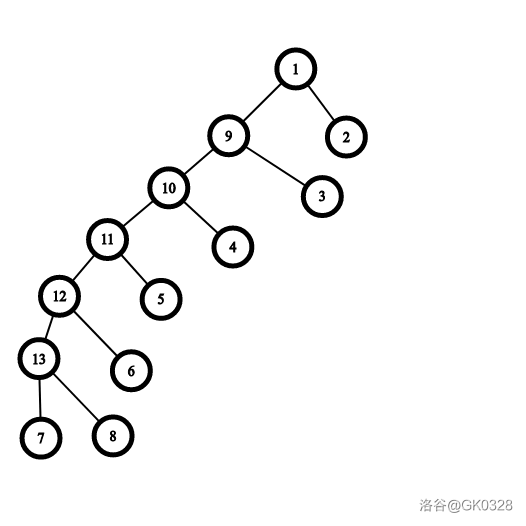
方案2:

以下代码中选择了方案二,这两种构造的节点数均\(\le 2n\)。(注意方案二构造时不能出现一个虚点只连一条边,否则节点数可能超过\(2n\),因为方案二正确的基础是含有\(k\)个叶子节点的满二叉树非叶子节点数量为\(k-1\),因此不允许出现链)。
我们建立的虚点可以看做是原树中根节点的复制节点,原树中两点在新树中\(lca\)为原树中\(lca\)的复制节点,但是计算时必须保证这些虚点不会被统计入答案中。
可以证明,对于一个\(d\)叉树,最大子树大小\(maxsize \le \frac{nd}{d+1}\)。
我们可以利用反证法,假设有一条边,使得这条边断掉后,子树\(x\)的\(size\)大于\(\frac{nd}{d+1}\),同时切断\(x\)的任意一颗子树都不成立。
根据切断\(x\)的任意一颗子树都不成立,那么每棵子树大小必须\(\le \lfloor\frac{n}{d+1}\rfloor\)(\((d+1)|n\)时不能取等号),由于\(d\)叉树每个节点度数最多为\(d+1\),切断一条边后度数为\(d\),因此:
那么二叉树选择最优边后\(maxsize \le \frac{2n}{3}\),分治时间复杂度为\(O(n \log n)\)级别(准确为\(O(n \log_{1.5} n)\),比点分治多一个常数)。
在本题中,先转化式子:
我们每次枚举一条边(长度为\(w\))进行分治,我们需要统计这条边两端所有点的贡献,假设一条边的两端的子树为\(T_x,T_y\),那么我们以两个连通块中这条边的两个端点为两棵子树的根计算\(T_x,T_y\)之间的贡献。
我们\(dfs\)出两棵子树中每个点的深度(相对于我们钦定的根,记为\(dep1_x\)或\(dep2_x\)),那么对于\(x_0 \in T_x,y_0 \in T_y\),它们的距离为\(dep1_{x_0}+w+dep2_{y_0}\)。
然后我们考虑统计第二棵树,由于不同层递归的树的大小不同,而总大小为\(n \log n\),所以我们考虑在第二棵树上建虚树。
由于我们边分治同点分治相同,不能同时选取同一棵子树内的链,我们把\(T_x\)中点染成黑色,\(T_y\)中点染成白色,那么转化成一个问题:在虚树上有一些黑点和白点,我们把任意一个点\(u\)的点权\(v_u\)定为\(dep_u+dep1/2_u\)。
求:
简单树形\(dp\)即可。
我们考虑时间复杂度,分治需要\(O(n \log n)\),建虚树排序\(\log n\),总时间复杂度\(O(n \log^2 n)\)。
但是我们可以去掉一个\(\log\)。
因为我们求解时,会先按照\(dfn\)排序,然后把所有点分成两部分递归,实际上我们只需要把已经按\(dfn\)排完的序列抽出\(col=0\)和\(col=1\)的两部分,它们已经有序了(也可以先分治到底,再进行归并排序,互为逆运算)。
那么时间复杂度变为\(O(n \log n)\)。
\(Code:\)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#define N 370005
#define M 740010
#define INF 1000000007
#define ll long long
#define pr pair<int,int>
#define mp make_pair
#define IT vector< pr > :: iterator
using namespace std;
const ll LLINF=-1919191919191919;
int n,tn,x,y,z,w;
int tot=1,ct,rt,rtsz,col[N],sz[M],dfn[N],fr[M],nxt[M << 1],d1[M << 1],d2[M << 1];
int cnt,bg[N],lg2[N << 1],st[N << 1][22];
int c[2][N];
ll ans,val[N],cdp[N],rdp[M],tdp[N],dep[N];
bool vis[M << 1];
vector< pr >e1[N],e2[N],e3[M];
void add_edge(int x,int y,int z)
{
tot++;
d1[tot]=y,d2[tot]=z;
nxt[tot]=fr[x],fr[x]=tot;
}
void add(int x,int y,int z)
{
add_edge(x,y,z),add_edge(y,x,z);
}
void dfs1(int u,int F)
{
for (IT it=e1[u].begin();it!=e1[u].end();++it)
{
int v=it->first;
if (v==F)
continue;
e3[u].push_back(*it);
dfs1(v,u);
}
}
void dfs2(int u,int F)
{
dfn[++ct]=u,st[++cnt][0]=u,bg[u]=cnt;
for (IT it=e2[u].begin();it!=e2[u].end();++it)
{
int v=it->first;
if (v==F)
continue;
tdp[v]=tdp[u]+it->second;
dep[v]=dep[u]+1;
dfs2(v,u);
st[++cnt][0]=u;
}
}
int lca(int x,int y)
{
x=bg[x],y=bg[y];
if (x>y)
swap(x,y);
int k=lg2[y-x+1];
return (dep[st[x][k]]<dep[st[y-(1 << k)+1][k]])?st[x][k]:st[y-(1 << k)+1][k];
}
void dfs3(int u,int F)
{
for (int i=fr[u];i;i=nxt[i])
{
int v=d1[i];
if (v==F)
continue;
cdp[v]=cdp[u]+d2[i];
dfs3(v,u);
}
}
namespace VT
{
int tot,fr[N],nxt[N << 1],d[N << 1];
int t,st[N];
ll dp1[N],dp2[N];
void add(int x,int y)
{
tot++;
d[tot]=y;
nxt[tot]=fr[x],fr[x]=tot;
}
void ins(int x)
{
if (!t)
{
st[++t]=x;
return;
}
int g=lca(x,st[t]);
while (t>1 && dep[st[t-1]]>dep[g])
add(st[t-1],st[t]),t--;
if (dep[g]<dep[st[t]])
add(g,st[t]),t--;
if (!t || st[t]!=g)
st[++t]=g;
st[++t]=x;
}
void dfs5(int u)
{
dp1[u]=dp2[u]=LLINF;
if (col[u]==0)
dp1[u]=val[u]; else
if (col[u]==1)
dp2[u]=val[u];
for (int i=fr[u];i;i=nxt[i])
{
int v=d[i];
dfs5(v);
ans=max(ans,dp1[u]+dp2[v]+w-(tdp[u] << 1LL));
ans=max(ans,dp2[u]+dp1[v]+w-(tdp[u] << 1LL));
dp1[u]=max(dp1[u],dp1[v]),dp2[u]=max(dp2[u],dp2[v]);
}
}
void Clear(int u)
{
col[u]=-1,val[u]=0;
for (int i=fr[u];i;i=nxt[i])
{
int v=d[i];
Clear(v);
}
fr[u]=0;
}
};
void getrt(int u,int F,int rn)
{
sz[u]=1;
for (int i=fr[u];i;i=nxt[i])
{
int v=d1[i];
if (v==F || vis[i])
continue;
getrt(v,u,rn);
sz[u]+=sz[v];
if (max(sz[v],rn-sz[v])<rtsz)
rtsz=max(sz[v],rn-sz[v]),rt=i;
}
}
void dfs4(int u,int F,int opt)
{
if (u<=tn)
val[u]=rdp[u]+cdp[u],col[u]=opt;
for (int i=fr[u];i;i=nxt[i])
{
int v=d1[i];
if (v==F || vis[i])
continue;
rdp[v]=rdp[u]+d2[i];
dfs4(v,u,opt);
}
}
void solve(int u,int s,int l,int r)
{
if (l>=r)
return;
rtsz=INF;
getrt(u,0,s);
if (rtsz==INF)
return;
vis[rt]=vis[rt^1]=true;
rdp[d1[rt]]=0,rdp[d1[rt^1]]=0;
dfs4(d1[rt],0,0),dfs4(d1[rt^1],0,1),w=d2[rt];
VT::t=0;
for (int i=l;i<=r;++i)
VT::ins(dfn[i]);
for (int i=VT::t;i>1;--i)
VT::add(VT::st[i-1],VT::st[i]);
VT::dfs5(VT::st[1]);
VT::tot=0;
c[0][0]=c[1][0]=0;
for (int i=l;i<=r;++i)
c[col[dfn[i]]][++c[col[dfn[i]]][0]]=dfn[i];
int L=l-1;
for (int i=0;i<2;++i)
for (int j=1;j<=c[i][0];++j)
dfn[++L]=c[i][j];
VT::Clear(VT::st[1]);
int k=rt,mid=l+c[0][0]-1,ts=s-sz[d1[k]];
solve(d1[k],sz[d1[k]],l,mid),solve(d1[k^1],ts,mid+1,r);
}
int main()
{
scanf("%d",&n),tn=n;
for (int i=1;i<n;++i)
{
scanf("%d%d%d",&x,&y,&z);
e1[x].push_back(mp(y,z));
e1[y].push_back(mp(x,z));
}
for (int i=1;i<n;++i)
{
scanf("%d%d%d",&x,&y,&z);
e2[x].push_back(mp(y,z));
e2[y].push_back(mp(x,z));
}
dfs1(1,0);
dep[1]=1,tdp[1]=0,dfs2(1,0);
lg2[0]=-1;
for (int i=1;i<=cnt;++i)
lg2[i]=lg2[i >> 1]+1;
for (int j=1;j<=lg2[cnt];++j)
for (int i=1;i<=cnt-(1 << j)+1;++i)
st[i][j]=(dep[st[i][j-1]]<dep[st[i+(1 << j-1)][j-1]])?st[i][j-1]:st[i+(1 << j-1)][j-1];
for (int i=1;i<=n;++i)
e1[i].clear(),e2[i].clear();
for (int i=1;i<=n;++i)
{
int len=e3[i].size();
if (len<=2)
{
for (IT it=e3[i].begin();it!=e3[i].end();++it)
add(i,it->first,it->second);
} else
if (len==3)
{
int L=++n,j=0;
add(i,L,0);
for (IT it=e3[i].begin();it!=e3[i].end();++it,++j)
if (j & 1)
add(i,it->first,it->second); else
e3[L].push_back(*it);
} else
{
int L=++n,R=++n,j=0;
add(i,L,0),add(i,R,0);
for (IT it=e3[i].begin();it!=e3[i].end();++it,++j)
if (j & 1)
e3[R].push_back(*it); else
e3[L].push_back(*it);
}
e3[i].clear();
}
for (int i=1;i<=tn;++i)
col[i]=-1;
dfs3(1,0);
solve(1,n,1,tn);
ans >>=1LL;
for (int i=1;i<=tn;++i)
ans=max(ans,cdp[i]-tdp[i]);
printf("%lld\n",ans);
return 0;
}


