【CodeForces 117C】Cycle

链接：

洛谷

题目大意：

在一个没有自环的有向图找出一个长度为三的环。

\(n\leq5000\)。

正文：

暴力 \(\mathcal{O}(n^3)\)，直接枚举 \(i,j,k\)，或者是预处理一个反图，再通过枚举 \(i,j\)，找能到达 \(i\) 的点和 \(j\) 能到达的点的交集。

这种方法就是通过已知的边 \((i,j)\) 找另一个点 \(k\)。考虑优化它。

\(i\) 能到达很多个 \(j\)，时间就花在这里，每次就要枚举 \(O(n)\) 条边。

所以我们要通过性质，尝试能否删掉一些边。

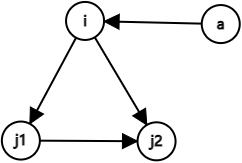
当新的一点 \(a\) 连接 \(i\) 时，假设 \(a\) 连向 \(j_1\)，形成 \((i,j_1,a)\) 的环，若 \(j_1\) 连向 \(a\)，形成 \((i,j_2,a)\) 的环。

那么 \((i,j_2)\) 边就没用了。综上所述，每个点的出边就只有一条了。

代码:

const int N = 5010;

inline ll READ()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n;
char a[N][N];
int e[N];

int main()
{
//	freopen(".out", "r", stdin);
	n = READ();
	for (int i = 1; i <= n; i++)
			scanf("%s", a[i] + 1);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			if (a[i][j] == 49 && (!e[i] || a[j][e[i]] == 49)) e[i] = j;
	
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			if (a[e[i]][j] == 49 && a[j][i] == 49)
			{
				printf ("%d %d %d\n", i, e[i], j);
				return 0;
			}
	printf ("-1\n");
	return 0;
}