【学习笔记】点分治
点分治:
引出:
给定一个 \(n(n\leq 10^4)\) 个节点的树,树枝有边权,求距离不超过 \(k\) 的点的对数。
求解:
直接 \(\mathcal{O}(n^2)\) 行不通,我们要想一个更快的方法。
考虑用点分治。我们先把任意一点作为根节点 \(rt\) 分出若干子树。如图,绿点就是两个合法方案:
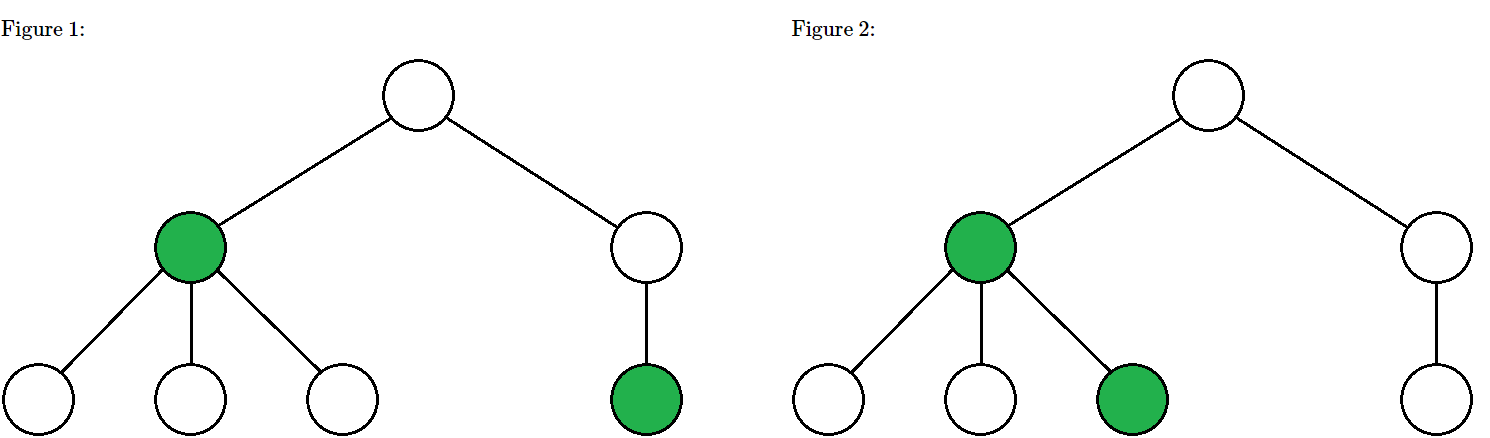
这样就能得到两种情况:
- 点对处于同一个子树。
- 点对处于不同子树。
对于情况一,我们可以把它看作是一个与原问题相同的子问题,可以递归求解!
然后是情况二,直接求解不同子树方案数有点困难,但是,我们对于相同子树的方案数就容易了。所以可以运用前缀和的思想,用总共合法方案数减去来自相同子树的方案数就是答案了。
但是这还是不够优秀,这在最坏的情况下是 \(\mathcal{O}(n^3\log n)\) 的,比暴力还暴力。考虑优化,从问题本身思考,我们慢主要是因为递归的层数太多了,想办法优化这里。
要让递归层数变小,就不能拿任意一点作根节点,要用树的重心(说白了就是让节点数最多的子树节点数最小),这样由重心划出的子树的节点数都不会超过树的大小的一半。
懒得证明了。总而言之,每次用中心作根节点的总复杂度就是 \(\mathcal{O}(n\log^2 n)\) 了。
代码:
const int N = 4e4 + 10;
int n;ll k;
struct edge
{
int to, nxt, val;
}e[N << 1];
int head[N], tot;
void Add(int u, int v, int w) {e[++tot] = (edge){v, head[u], w}, head[u] = tot;}
bool vis[N];
ll sz[N], son[N];
ll rt, sum;
void getRoot(int u, int fa)
{
sz[u] = 1, son[u] = 0;
for (int i = head[u], v; i; i = e[i].nxt)
{
v = e[i].to;
if (vis[v] || v == fa) continue;
getRoot(v, u);
sz[u] += sz[v];
son[u] = max(son[u], sz[v]);
}
son[u] = max(son[u], sum - sz[u]);
if (son[u] < son[rt]) rt = u;
}
ll dis[N], dissort[N], cnt;
ll ans;
void getDis(int u, int fa)
{
dissort[++cnt] = dis[u];
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || vis[v]) continue;
dis[v] = dis[u] + e[i].val;
getDis (v, u);
}
}
ll solve (int u, int w)
{
cnt = 0; dis[u] = w; getDis(u, 0);
sort (dissort + 1, dissort + 1 + cnt);
int l = 1, r = cnt;ll ans = 0;
while (l <= r)
if (dissort[r] + dissort[l] <= k)
ans += r - l, l++;
else
r--;
return ans;
}
void calc (int u)
{
vis[u] = 1; ans += solve(u, 0);
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (vis[v]) continue;
ans -= solve (v, e[i].val);
//Figure 1:
sum = sz[v], son[0] = n, rt = 0;
getRoot(v, u), calc(rt);
}
}
int main()
{
scanf ("%d", &n);
for (int i = 1; i < n; i++)
{
int u, v, w;
scanf ("%d%d%d", &u, &v, &w);
Add(u, v, w), Add(v, u, w);
}
scanf ("%lld", &k);
son[0] = sum = n, getRoot(1, 0), calc(rt);
printf ("%lld\n", ans);
return 0;
}
例题:
求解:
和上一道题一样。看代码理解吧。
代码:
const int N = 4e4 + 10, K = 1e7 + 10;
int n;ll k;
int m;
struct edge
{
int to, nxt, val;
}e[N << 1];
int head[N], tot;
void Add(int u, int v, int w) {e[++tot] = (edge){v, head[u], w}, head[u] = tot;}
bool vis[N];
ll sz[N], son[N];
ll rt, sum;
void getRoot(int u, int fa)
{
sz[u] = 1, son[u] = 0;
for (int i = head[u], v; i; i = e[i].nxt)
{
v = e[i].to;
if (vis[v] || v == fa) continue;
getRoot(v, u);
sz[u] += sz[v];
son[u] = max(son[u], sz[v]);
}
son[u] = max(son[u], sum - sz[u]);
if (son[u] < son[rt]) rt = u;
}
ll dis[N], CanGet[N], FaTree[N], cnt, Query[N];
ll ans;
bool num[K];
void getDis(int u, int fa, int Rt)
{
CanGet[++cnt] = u;
FaTree[u] = Rt;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == fa || vis[v]) continue;
dis[v] = dis[u] + e[i].val;
getDis (v, u, Rt);
}
}
bool cmp (int x, int y) {return dis[x] < dis[y];}
void solve (int u)
{
cnt = 0;
CanGet[++cnt] = u;
FaTree[u] = u;
dis[u] = 0; getDis(u, 0, u);
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (vis[v]) continue;
dis[v] = dis[u] + e[i].val;
getDis (v, u, v);
}
sort (CanGet + 1, CanGet + 1 + cnt, cmp);
for (int i = 1; i <= m; i++)
{
int l = 1, r = cnt;
if (num[i]) continue;
while (l < r)
{
if (dis[CanGet[l]] + dis[CanGet[r]] > Query[i]) {r--;}
else
{
if (dis[CanGet[l]] + dis[CanGet[r]] < Query[i]) {l++;}
else
{
if (FaTree[CanGet[l]] == FaTree[CanGet[r]])
{
if (dis[CanGet[r]] == dis[CanGet[r - 1]]) r--;
else l++;
}else
{
num[i] = 1; break;
}
}
}
}
}
}
void calc (int u)
{
vis[u] = 1; solve(u);
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (vis[v]) continue;
solve (v);
//Figure 1:
sum = sz[v], son[0] = n, rt = 0;
getRoot(v, u), calc(rt);
}
}
int main()
{
scanf ("%d%d", &n, &m);
for (int i = 1; i < n; i++)
{
int u, v, w;
scanf ("%d%d%d", &u, &v, &w);
Add(u, v, w), Add(v, u, w);
}
for (int i = 1; i <= m; i ++) scanf ("%lld", &Query[i]);
calc (1);
for (int i = 1; i <= m; i++)
if (num[i]) puts("AYE");
else puts("NAY");
return 0;
}


