字符串算法小结
AC 自动机:
介绍:
用 Trie 维护模式串的前缀。
自动机快速的原因就在于失配指针 \(\mathrm{fail}_i\),它指向 \(i\) 的最长后缀。
对于构建 \(\mathrm{fail}_i\),找到其父节点 \(\mathrm{fa}\),一直跳 \(\mathrm{fail}\),直到跳到根节点或某点有连过和 \(i\) 相同的字符。
代码:
const int N = 1e6 + 10;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
int n;
namespace AC
{
int t[N][30], e[N], fail[N];
int tot;
void Insert(char *s)
{
int p = 0, len = strlen(s);
for (int i = 0; i < len; i++)
{
int ch = s[i] - 'a';
if (!t[p][ch]) t[p][ch] = ++tot;
p = t[p][ch];
}
e[p]++;
}
queue <int> q;
void Build()
{
while(!q.empty()) q.pop();
for (int i = 0; i < 26; i++)
if (t[0][i]) q.push(t[0][i]);
while (!q.empty())
{
int p = q.front(); q.pop();
for (int i = 0; i < 26; i++)
if (t[p][i])
fail[t[p][i]] = t[fail[p]][i], q.push(t[p][i]);
else
t[p][i] = t[fail[p]][i];
}
}
int Query(char *s)
{
int p = 0, ans = 0, len = strlen(s);
for (int i = 0; i < len; i++)
{
p = t[p][s[i] - 'a'];
for(int j = p; j && e[j] != -1; j = fail[j])
ans += e[j], e[j] = -1;
}
return ans;
}
}
char s[N];
int main()
{
n = Read();
for (int i = 1; i <= n; i++)
scanf ("%s", s), AC::Insert(s);
AC::Build();
scanf("%s", s);
printf ("%d\n", AC::Query(s));
return 0;
}
Manacher 算法:
Manacher 算法,经常被称作马拉车,可以以 \(\mathcal{O}(n)\) 的时间复杂度求出字符串关于回文子串一类的问题。
介绍:
首先举个例子,设字符串 \(s=\texttt{bbdkd}\)。
在这里面,有偶回文子串 \(\texttt{bb}\)、奇回文子串 \(\texttt{dkd}\),在计算的过程中还要对奇偶问题进行讨论太过于麻烦,所以可以在每个字符之间加入特殊字符(首尾特殊字符可以作边界):
再设 \(R_i\) 表示以第 \(i\) 位字符为中心的最长回文的半径。对应上面的 \(s'\) 可以得到:
可以发现,以 \(i\) 为中心的最长回文子串长度就是 \(R_i-1\)。
我们在求解 \(R\) 数组的过程中再设 \(p,mx\) 分别表示当前回文子串中心和回文子串的右端点。若正在计算 \(R_i\),令 \(i\) 关于 \(p\) 的对称点 \(j=2p-i\)。然后为了先给 \(R_i\) 定下界,进行分类讨论(结合图片思考):
- \(mx\leq i\),因为恒有 \(R_i\geq 1\),所以 \(R_i\) 下界是 \(1\)。
- \(mx-i>R_j\),\(j\) 的左端点没有包裹住 \(p\) 的左端点(即以 \(j\) 为中心的回文子串被包含与 \(p\) 的)。因为是对称点,所以以 \(i\) 为中心的回文子串也一定被包含与 \(p\) 的,所以 \(R_i\) 下界为 \(R_j\)。
- \(mx-i\leq R_j\),\(j\) 的左端点包裹住了 \(p\) 的左端点(即以 \(j\) 为中心的回文子串不被包含与 \(p\) 的)。因为不被包含,所以不能保证在 \(mx'\) 以前的字符和 \(i\) 的对应,所以下界是 \(mx-i\)。
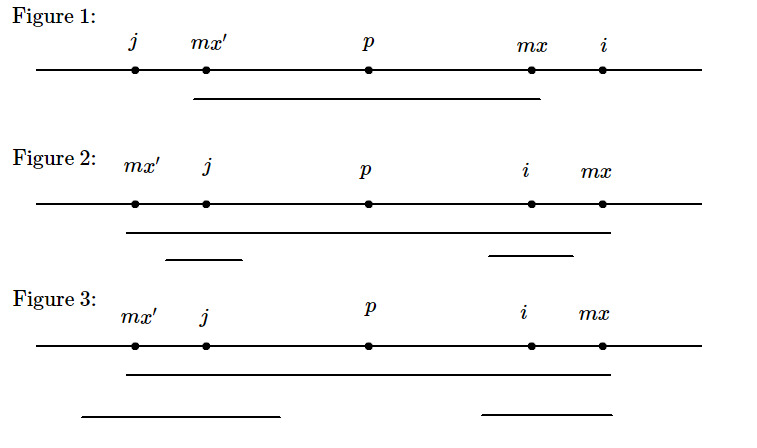
简单来说,定下界就是取 \(\min(mx-i,R_j)\)。
定完下界后,再往两边枚举检测一遍。
由于向左右拓展成功必然会导致 \(mx\) 向右移,而 \(mx\) 向右移不超过 \(n\) 次,故向左右拓展操作的总时间复杂度是 \(\mathcal{O}(n)\)。枚举 \(i\) 也是\(\mathcal{O}(n)\) 的,那么 Manacher 算法时间复杂度是 \(\mathcal{O}(n)\)。
代码:
int p = 1, mx = 1;
for (int i = 1; i <= n; i++)
{
R[i] = min (mx - i, R[2 * p - i]);
while (s[i - R[i]] == s[i + R[i]]) ++R[i];
if (i + R[i] > mx)
mx = i + R[i], p = i;
}
例题:
回文自动机:
回文自动机,又称回文树,也可以处理部分回文类问题。
介绍:
回文树是一棵由两棵分别为奇、偶的树构成的森林。
其中,奇树用于存储长度为奇数的回文串;偶树用于存储长度为偶数的回文串。
每个节点可以维护该节点字符串长度、该节点出边连接到的节点、失配指针。
如图:
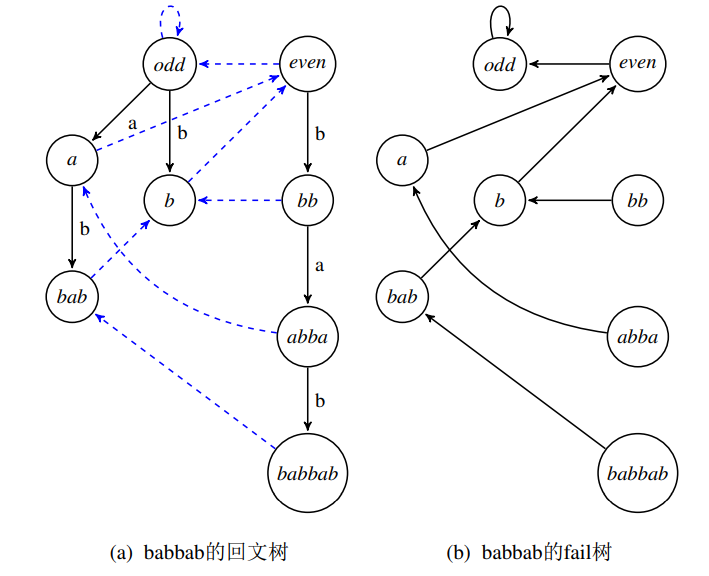
构造方法 - 基础插入方法:
有定理:以新加入的字符 \(c\) 为结尾的,未在 \(s\) 中出现过的回文子串最多只有 \(1\) 个,且必为 \(sc\) 的最长回文后缀。那么构造时,求出 \(sc\) 的最长回文后缀即可。于是现在要在 \(s\) 的最长回文后缀对应的失配链中找到长度最大的一个节点 \(t\),使得 \(s_{|s|-\mathrm{len}(t)}=c\),则 \(sc\) 的最长回文后缀即为 \(ctc\)。
也因此,新建节点时的失配指针要连向最长的 \(t\) 满足 \(s_{|s|-\mathrm{len}(t)}=c\) 的节点,若 \(\mathrm{len}(t)=-1\) 则连偶树根。
代码:
const int N = 5e5 + 10;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
char s[N];
namespace PAM
{
int len[N], fail[N], s[N], t[N][27];
int lst, tot = -1, n = 0;
int sum[N];
int New(int x)
{
len[++tot] = x;
return tot;
}
void Build()
{
New(0), New(-1);
fail[0] = 1;
s[0] = -1;
}
int Find(int x)
{
while (s[n - 1 - len[x]] != s[n])
x = fail[x];
return x;
}
void Insert(int x)
{
s[++n] = x;
int cur = Find(lst);
if (!t[cur][x])
{
int now = New(len[cur] + 2),
tmp = Find(fail[cur]);
fail[now] = t[tmp][x];
sum[now] = sum[fail[now]] + 1;
t[cur][x] = now;
}
lst = t[cur][x];
}
}
int main()
{
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
scanf ("%s", s + 1);
int len = strlen(s + 1);
PAM::Build();
for (int i = 1, lst = 0; i <= len; i++)
{
PAM::Insert((s[i] - 97 + lst) % 26 + 97 - 'a');
printf ("%d ", lst = PAM::sum[PAM::lst]);
}
return 0;
}
后缀数组:
倍增:
注意:本文第 \(i\) 个后缀是指关于原字符串 \(S\) 的子串 \(S_{i\cdots\text{len}}\)。
后缀数组 \(\mathrm{SA}\) 就是以此存储将 \(s\) 的 \(n\) 个后缀从小到大排序后的数组。即:排名为 \(i\) 的后缀是哪一个。
名次数组 \(\mathrm{Rank}\) 和 \(\mathrm{SA}\) 的互逆,它储存的是第 \(i\) 个后缀的排名。
求出后缀数组 \(\mathrm{SA}\),一般使用倍增的方法:用倍增对每个字符开始的长度 \(2^k\) 的子字符串进行排序,得到 \(\mathrm{Rank}\)。\(k\) 从 \(0\) 开始,每次加一,当 \(2^k\) 大于 \(n\) 就一定能比较出大小。每次排序利用上一次长度为 \(2^{k-1}\) 的两个字符串排名作为两个部分,然后基数排序,就能得到长度为 \(2^k\) 的字符串的排名。如图举例子:

其中 \(x,y\) 就分别是前半部分和后半部分。这两个部分正好在基数排序中看作是两位。然后假设后半部分已经有序,而且前半部分排名相同的必然在倍增后排名依然为连续一段,所以我们可以求出前半部分每个排名倍增后所在的区间。接着,倒序枚举后半部分,并依次在所在区间末尾插入即可。
也可以从上图得知倍增是 \(i\) 的前半部分其实就是倍增前 \(i\) 的排名,其后半部分就是就是将要合并的第二部分的起始位置。
还有一点:
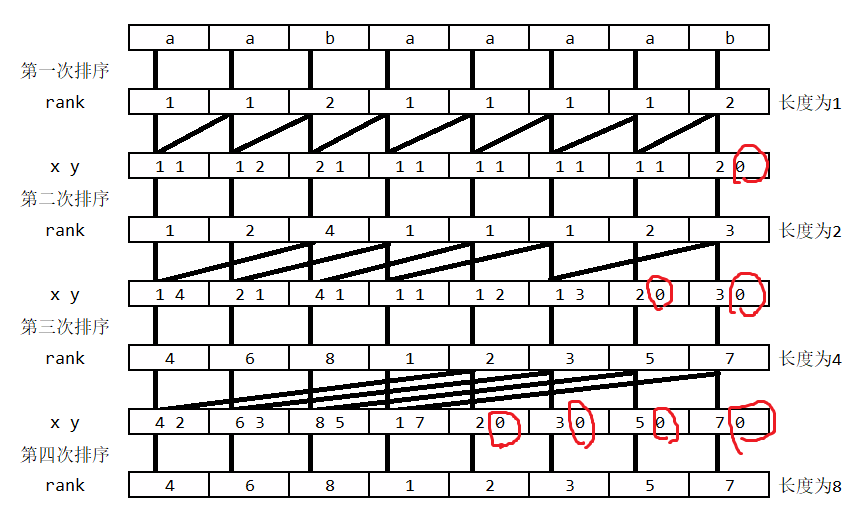
如图红圈,有的位置在合并过程中已经没有了后半部分,我们把它当作是该前半部分最小的,这里有点难理解,由于两个部分在基数排序中看作是两位数,换句话说这里的意思就是个位当作是 \(0\),就成了该十位中最小的数。
倍增代码:
int n, m;
int sa[N], c[N], x[N], y[N];
char s[N];
void Solve()
{
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //The numer has no the latter part
for (int i = 1; i <= n; i++)
if(sa[i] > k) y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k])? num: ++num;
m = num;
if (n == m) break;
}
return ;
}
int main()
{
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
scanf ("%s", s + 1);
n = strlen(s + 1), m = 122;
Solve();
for (int i = 1; i <= n; i++)
printf ("%d ", sa[i]);
return 0;
}
height 数组:
定义 \(\mathrm{height}_i\) 是第 \(\mathrm{SA}_i\) 个后缀和第 \(\mathrm{SA}_{i-1}\) 个后缀的最长公共前缀的长度。那么第 \(j\) 个后缀与第 \(k\) 个后缀(\(\mathrm{Rand}_j<\mathrm{Rand}_k\))的最长公共前缀为:
那么在实际应用时,我们就可以通过这个数组得到 LCP 了。
既然这样,那如何快速求出它呢?定义 \(h_i\) 表示第 \(i\) 个后缀与其排名减一的后缀的 LCP 长度,即 \(h_i=\mathrm{height}_{\mathrm{Rand}_i}\)。\(h_i\) 有一个性质,即 \(h_i\geq h_{i-1}-1\)。
证明性质:
设第 \(j\) 个后缀时排在第 \(i-1\) 个后缀前一名的后缀,其 LCP 长度为 \(h_{i-1}\),那么第 \(j+1\) 个后缀时排在第 \(i\) 个后缀前面,且其 LCP 长度为 \(h_{i-1}-1\),所以 \(h_{i}\) 至少是 \(h_i\)。
证毕。
求解代码:
int sa[N], Rank[N], height[N];
char s[N];
void calHeight()
{
for (int i = 1; i <= n; i++) Rank[sa[i]] = i;
int h = 0, j;
for (int i = 1; i <= n; height[Rank[i++]] = h)
for (h? h--: 0, j = sa[Rank[i] - 1]; s[i + h] == s[j + h]; h++);
return;
}
后缀自动机:
一个很强大的字符串处理的算法。
介绍:
一个后缀自动机,实际上是一个字符串的压缩的后缀字典树。
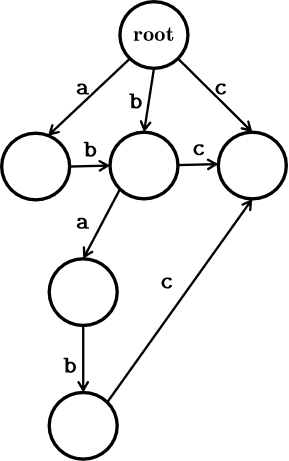
如图,这是 \(\texttt{ababc}\) 串的后缀字典树。
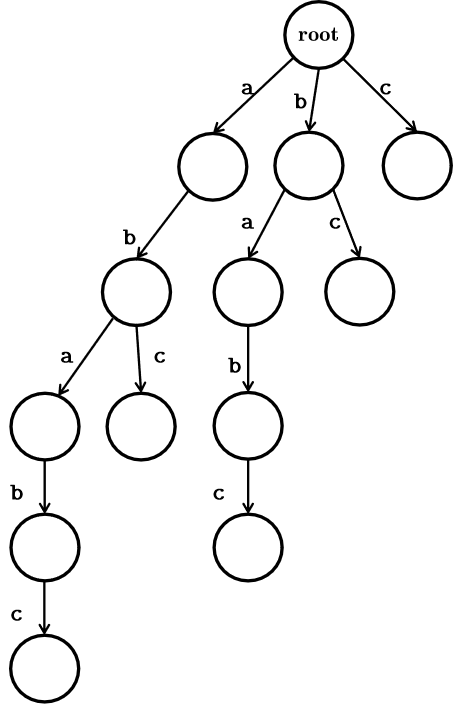
后缀字典树是 \(\mathcal{O}(n^2)\) 级的,考虑压缩。
可以发现,子串 \(\texttt{a}\underline{\texttt{babc}}\) 的状态和 \(\texttt{babc}\) 的状态是完全相同的,那么就可以压缩成:
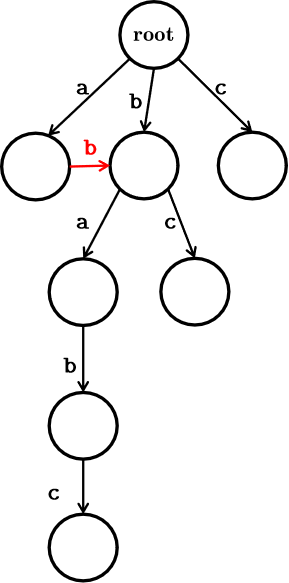
最终变成: