多项式大总结
文章没有写完，近期填完这坑
参考文章：
https://www.luogu.com.cn/blog/froggy/duo-xiang-shi-tai-za-hui
https://www.cnblogs.com/zwfymqz/p/8244902.html
https://www.cnblogs.com/RabbitHu/p/FFT.html
https://blog.csdn.net/enjoy_pascal/article/details/81478582
Thomas H.Cormen,Charles E.Leiserson,Ronald L.Rivest,Clifford Stein. 殷建平等译. 算法导论第三版 [M]. 北京:机械工业出版社,2013,527-542.
多项式的定义：
一个 \(n\) 次多项式，是长成这样的：
其中 \(a_i\) 是第 \(i\) 项的系数。
拉格朗日插值法：
给定 \(n\) 个点 \((x_i,y_i)\) 确定一个多项式 \(f(k)\)，并求出 \(f(k)\) 的值。
定理：
不会证明这个。
代码：
int n;
ll x[N], y[N], k;
ll ans;
ll qpow(ll a, ll b)
{
ll ans = 1;
for (; b; b >>= 1, a = a * a % mod)
if (b & 1) ans = ans * a % mod;
return ans;
}
int main()
{
scanf ("%d%lld", &n, &k);
for (int i = 1; i <= n; i++)
scanf ("%lld%lld", &x[i], &y[i]);
for (int i = 1; i <= n; i++)
{
ll tmp = y[i];
for (int j = 1; j <= n; j++)
if(i != j)
tmp = tmp * ((k - x[j] + mod) % mod) % mod * qpow((x[i] - x[j] + mod) % mod, mod - 2) % mod;
ans = (ans + tmp) % mod;
}
printf ("%lld\n", ans);
return 0;
}
快速傅里叶变换 FFT：
为了方便计算，这里的 \(n\) 都是 \(2\) 的整次幂。
在此之前，先明白 DFT（离散傅里叶变换）、FFT（快速傅里叶变换）、IDFT（离散傅里叶逆变换）、IFFT（快速傅里叶逆变换） 之间的关系：
类似的，IDFT 也是概念，IFFT 是基于 IDFT 概念的算法。现在不知道这四个东西的具体含义在下文介绍。
给定两个多项式 \(F(x),G(x)\)，求出它们的卷积 \(F(x)*G(x)\)。
这里定义多项式卷积运算：
然后快速傅里叶变换可以在 \(\mathcal{O}(n\log n)\) 的时间复杂度内完成多项式乘法。
多项式的点值表示：
点值表示法，顾名思义就是把用 \(n\) 点的坐标表示一个多项式：
而点值表示法的优点就是可以在 \(\mathcal{O}(n)\) 的时间范围内求出两个多项式的乘积。
多项式的系数表示：
系数表示法，就是记录 \(F(x)\) 每一项的系数，比如 \(F(x)=\sum_{i=0}^{n-1}a_ix^i\) 可以表示为：
那么我们可以推测，多项式乘法流程一般是：系数表示法先转化到点值表示法，这样就能快速卷积，然后由转回系数表示法。也就是有两步，第一步系数转点值就是 DFT；第二步点值转系数 IDFT。
复数：
介绍：
提示：建议学习数学选修 2-2 的复数相关课程。
\(i\) 是虚数单位，规定：
- \(i^2=-1\)；
- 实数可以与它进行四则运算，进行四则运算时，原有的加法和乘法运算律仍然成立。
有一个复数 \(z=a+bi(a,b\in\mathbb{R})\)，其中 \(a,b\) 分别是 \(z\) 的实部与虚部。那么在复平面对应的平面直角坐标系中，\(z\) 在 \((a,b)\)：
如图点 \(Z\) 的复数是 \(z=3+4i\)，它对应的平面直角坐标系中在 \((3,4)\)。
或者，你还可以把复数作成一个向量：
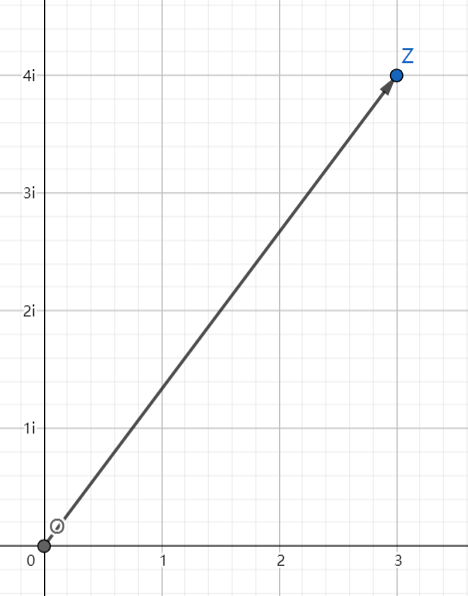
向量 \(\overrightarrow{OZ}\) 与复数 \(z=a+bi\) 一一对应。然后有：
共轭复数：
一般地，当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数。通常记复数 \(z\) 的共轭复数为 \(\overline{z}\)。
比如当 \(z=a+bi\) 时，\(\overline{z}=a-bi\)。
复数的运算：
设 \(z_1=a+bi,z_2=c+di\) 是任意两个复数，那么：
其中，复数相乘时，模长相乘，幅角相加。
DFT：
其实 DFT 的本质就是代入 \(x\) 得到点值，而这几个 \(x\) 就是一些特殊的复数（选择这些复数的原因不会证明/youl）。
单位根：
在复平面中，以原点为圆心，半径为 \(1\) 的圆是 单位圆。然后将这个圆 \(n\) 等分，以圆心为起点，圆的 \(n\) 等分点为终点，做 \(n\) 个向量，设幅角为正且最小的向量对应的复数是 \(\omega_n\)，也就是 \(n\) 次单位根。根据复数乘法性质，剩下 \(n-1\) 个复数是 \(\omega_n^2,\omega_n^3,\dots,\omega_n^n\)。其中，这几个复数的值是：
这几个复数就是那几个 “特殊的复数”。
单位根的性质：
性质一：
证明：
性质二：
证明：
FFT 的流程：
朴素的 DFT 是 \(\mathcal{O}(n^2)\) 的，通过分治优化 DFT 得到 FFT。
设多项式 \(F(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}\)，然后按照奇偶性分为两份：
设：
那么：
将 \(x=\omega_n^k\quad(k<\frac{n}{2})\) 代入得：
将 \(x=\omega_n^{k+\frac{n}{2}}\) 代入得：
然后我们就可以通过 \(\mathcal{O}(n\log n)\) 的时间复杂度递归了。
IFFT 的流程：
我们得到了点值表示 \(F(x)=\{(\omega_n^0,F(\omega_n^0)),(\omega_n^1,F(\omega_n^1)),\cdots,(\omega_n^{n-1},F(\omega_n^{n-1}))\}\)。设：\(y_k=\sum_{i=0}^{n-1}a_i\cdot\omega_n^{ki}\)，我们要求系数：
关于证明，stoorz 爷的看法：
QuantAsk 爷的看法：
虽然二位爷都对我进行嘲讽，但这不影响我们证明。
将 \(y_i\) 的定义代入后面的和式得到：
发现最后的和式是等比数列求和。设 \(S(\omega_n^k)=\sum_{i=0}^{n-1}(\omega_n^k)^i\quad(k>0)\)，用等比数列求和公式代入：
而 \(S(\omega_n^0)\) 更好求了：
代回原式：
\(a_i=\frac{1}{n}\sum_{j=0}^{n-1}y_j\cdot\omega_n^{-ij}\) 得证。
所以 IFFT 只用用对点值表示的 \(F(x)\) 像 FFT 一样操作，只不过乘的是原来的复数的共轭，就可以求出系数表示的多项式了。
蝴蝶变换优化：
递归 FFT 常数大，所以尝试把它变成迭代形式。
按奇偶性划分可以发现一个规律：
| 十进制 | 二进制 |
|---|---|
| \(0~1~2~3~4~5~6~7\) | \(000~001~010~011~100~101~110~111\) |
| \(0~2~4~6,1~3~5~7\) | \(000~010~100~110,001~011~101~111\) |
| \(0~4,2~6,1~5,3~7\) | \(000~100,010~110,001~101,011~111\) |
| \(0,4,2,6,1,5,3,7\) | \(000,100,010,110,001,101,011,111\) |
每一个数最终的位置，就是把它的二进制翻转过来。
所以每个数的位置就能够 \(\mathcal{O}(n)\) 预处理出来（递推式见代码 tr[i])。
代码：
const int N = 1500010;
const double PI = acos(-1.0);
struct Complex
{
double x, y;
Complex (double ix, double iy) {x = ix, y = iy;}
Complex () {x = y = 0;}
Complex operator + (Complex &b)
{
return Complex(x + b.x, y + b.y);
}
Complex operator - (Complex &b)
{
return Complex(x - b.x, y - b.y);
}
Complex operator * (Complex &b)
{
return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
}
}f[N << 1], g[N << 1];
int n, m;
int tr[N << 1];
void FFT (Complex *f, bool isDFT)
{
for (int i = 1; i <= n; i++)
if (i < tr[i]) swap (f[i], f[tr[i]]);
for (int p = 2; p <= n; p <<= 1)
{
int len = p >> 1;
Complex omega(cos(2 * PI / p), sin(2 * PI / p));
if (!isDFT) omega.y *= -1; //共轭复数
for (int k = 0; k < n; k += p)
{
Complex tmp(1, 0);
for (int i = k; i < k + len; i ++)
{
Complex y = tmp * f[i + len];
f[i + len] = f[i] - y;
f[i] = f[i] + y;
tmp = tmp * omega;
}
}
}
if(!isDFT) for (int i = 0; i <= n; i++) f[i].x /= n;
}
int main()
{
scanf ("%d%d", &n, &m);
for (int i = 0; i <= n; i++)
scanf ("%lf", &f[i].x);
for (int i = 0; i <= m; i++)
scanf ("%lf", &g[i].x);
for (m += n, n = 1; n <= m; n <<= 1);
for (int i = 1; i <= n; i++)
tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0);
FFT(f, 1), FFT(g, 1);
for (int i = 0; i <= n; i++) f[i] = f[i] * g[i];
FFT(f, 0);
for (int i = 0; i <= m; i++)
printf ("%d ", (int)(f[i].x + 0.49));
return 0;
}
快速数论变换 NTT：
由于 FFT 会有很大的精度误差，所以用模数操作代替，就是 NTT 了，NTT 也比 FFT 要快很多。
原根的定义：
百度百科给的定义：
原根是一种数学符号，设 \(p\) 是正整数，\(g\) 是整数，若 \(g\) 模 \(p\) 的阶等于 \(\varphi(p)\)，则称 \(g\) 为模 \(p\) 的一个原根。
简单点说：
若整数 \(g\) 是奇素数 \(p\) 的一个原根，则满足 \(g,g^2,g^3,\cdots,g^{p-1}\) 在模 \(p\) 意义下互不相同。
在模 \(998244353\) 意义下最小原根 \(g=3\)!
NTT 的基本流程：
若 \(p\) 满足 \(2^k\cdot r+1\)（比如 \(998244353=2^{23}\times199+1\)），把 \(g^{\frac{p-1}{2^k}}\) 作为 \(\omega_n^1\)，发现原本单位根的性质它都能满足，那么就这么跑 FFT 可以了。
但 NTT 也有局限性，只能处理 \(n\leq 2^k\) 的情况，遇到模数 \(p=10^9+7\) 时，NTT 就做不了。所以后面有任意模数 NTT。
代码：
const int N = 1500010;
const ll mod = 998244353ll, G = 3, invG = 332748118ll;
ll f[N << 1], g[N << 1];
int n, m;
int tr[N << 1];
ll qpow(ll a, ll b)
{
ll ans = 1;
for (; b; b >>= 1, a = a * a % mod)
ans = ans * (b & 1? a: 1) % mod;
return ans;
}
void NTT (ll *f, bool isDFT)
{
for (int i = 1; i <= n; i++)
if (i < tr[i]) swap (f[i], f[tr[i]]);
for (int p = 2; p <= n; p <<= 1)
{
int len = p >> 1;
ll omega = qpow(isDFT? G: invG, (mod - 1) / p);
for (int k = 0; k < n; k += p)
{
ll tmp = 1ll;
for (int i = k; i < k + len; i ++)
{
ll y = tmp * f[i + len] % mod;
f[i + len] = (f[i] - y + mod) % mod;
f[i] = (f[i] + y) % mod;
tmp = tmp * omega % mod;
}
}
}
if(!isDFT)
{
ll invn = qpow(n, mod - 2);
for (int i = 0; i <= n; i++) f[i] = f[i] * invn % mod;
}
}
int main()
{
scanf ("%d%d", &n, &m);
for (int i = 0; i <= n; i++)
scanf ("%lld", &f[i]);
for (int i = 0; i <= m; i++)
scanf ("%lld", &g[i]);
for (m += n, n = 1; n <= m; n <<= 1);
for (int i = 1; i <= n; i++)
tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0);
NTT(f, 1), NTT(g, 1);
for (int i = 0; i <= n; i++) f[i] = f[i] * g[i];
NTT(f, 0);
for (int i = 0; i <= m; i++)
printf ("%lld ", f[i]);
return 0;
}
多项式乘法逆：
给定一个多项式 \(F(x)\) ，请求出一个多项式 \(G(x)\)， 满足 \(F(x) * G(x) \equiv 1\pmod{x^n}\)。系数对 \(998244353\) 取模。
思路：
运用倍增的思想求解。
设已经求出 \(G'(x)\equiv F(x)^{-1}\pmod{x^{\frac{n}{2}}}\)，将 \(G(x)\equiv F(x)^{-1}\pmod{x^n}\) 与之相减得：
式子两边同时取平方：
式子两边同时乘 \(F(x)\):
接着就可以套 NTT 求解了。
代码：
const int N = 1500010;
const ll mod = 998244353ll, G = 3, invG = 332748118ll;
ll f[N << 1], g[N << 1];
int n, m;
int tr[N << 1];
ll qpow(ll a, ll b)
{
ll ans = 1;
for (; b; b >>= 1, a = a * a % mod)
ans = ans * (b & 1? a: 1) % mod;
return ans;
}
void NTT (ll *f, bool isDFT, int n)
{
for (int i = 1; i <= n; i++)
if (i < tr[i]) swap (f[i], f[tr[i]]);
for (int p = 2; p <= n; p <<= 1)
{
int len = p >> 1;
ll omega = qpow(isDFT? G: invG, (mod - 1) / p);
for (int k = 0; k < n; k += p)
{
ll tmp = 1ll;
for (int i = k; i < k + len; i ++)
{
ll y = tmp * f[i + len] % mod;
f[i + len] = (f[i] - y + mod) % mod;
f[i] = (f[i] + y) % mod;
tmp = tmp * omega % mod;
}
}
}
if(!isDFT)
{
ll invn = qpow(n, mod - 2);
for (int i = 0; i <= n; i++) f[i] = f[i] * invn % mod;
}
}
ll h[N << 1];
void Inv(ll *f, ll *g, int m)
{
if (m == 1)
{
g[0] = qpow(f[0], mod - 2);
return ;
}
Inv(f, g, (m + 1) / 2);
int n;
for (n = 1; n < (m << 1); n <<= 1);
for (int i = 0; i <= n; i++)
tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0),
h[i] = f[i] * (i <= m);
NTT(h, 1, n), NTT(g, 1, n);
for (int i = 0; i <= n; i++)
g[i] = (2 - g[i] * h[i] % mod + mod) % mod * g[i] % mod;
NTT(g, 0, n);
for (int i = m; i <= n; i++) g[i] = 0;
}
int main()
{
scanf ("%d", &n);
for (int i = 0; i < n; i++)
scanf ("%lld", &f[i]);
Inv(f, g, n);
for (int i = 0; i < n; i++)
printf ("%lld ", g[i]);
return 0;
}
多项式对数函数：
给定一个多项式 \(F(x)\) ，请求出一个多项式 \(G(x)\)， 满足 \(G(x) \equiv \ln F(x)\pmod{x^n}\)。系数对 \(998244353\) 取模。
求导：
提示：建议学习数学选修 2-2 的导数相关课程。
瞬时变化率：
先咕到这罢!
