【YBTOJ】国际象棋

题目链接：

题目

题目大意：

给你边长分别为 \(n,m\) 的两个棋盘，将它们拼在一起，但是两个棋盘横纵各间隔 \(w,h\)。然后在这个畸形棋盘放 \(k\) 个互不能相吃的车，求方案数。

正文：

先考虑 \(n=m,h=0\)（或 \(w=0\)）的情况。因为车的攻击是一整行和一整列，那么我们逐行判断可以选择哪一个格子，这样就可以保证一列里没有重的。对于每一行我们的放置方法也自然是可以直接考虑的。设 \(f_{i,j}\) 表示 \(1\) 至 \(i\) 行已经放了 \(j\) 个车的方案数。则有转移方程 \(f_{i,j}=f{i-1,j-1}\times(n-j+1)\)，其中 \(n-j+1\) 就表示了当前一行还能放车的位置的个数。通过这个方法完美地解决了车的放置的问题。

---

考虑畸形情况。

将原棋盘分为三个部分：

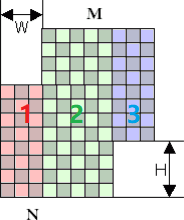
设 \(f_{i,x,y,z}\) 表示 \(1\) 至 \(i\) 行三个部分各放了 \(x,y,z\) 个车的方案数。然后像上文一样做就行了。

本题十分毒瘤，所以要高精度。

代码：

struct node   // 高精度
{
	int a[50];
    int &operator [](int x){return a[x];}
	node()
	{
		memset (a, 0, sizeof a);
	}
	inline void print()
	{
		for (int i = a[0]; i >= 1; i--)
			printf ("%d", a[i]);
	}
	
}f[N * 2][N][N][N], ans;

node operator +(node A, node B)  
{
	int s = 0, g = 0;
	node C;
	int len = max(A[0], B[0]);
	for (int i = 1; i <= len + 10; i++)
	{
		s = A[i] + B[i] + g, g = s / 10;
		C[i]= (s % 10);
		if (!s && !g && i > len) break;
		C[0] = i; 
	}
	return C;
}

node operator * (node A, ll a)  
{
	int s = 0, g = 0;
	node C;
	int len = A[0];
	for (int i = 1; i <= len + 10; i++)
	{
		s = A[i] * a + g, g = s / 10;
		C[i] = s % 10;
		if (!s && !g && i > len) break;
		C[0] = i; 
	}
	return C;
}

int n, m, w, h, k, W, H;

bool check(int x, int y)
{
    if (x <= n && y <= n) return 1;
    if (x > w && x <= w + m && y > h && y <= h + m) return 1;
    return 0;
}

int main()
{
	scanf ("%d%d%d%d%d", &n, &m, &w, &h, &k);
	if (w >= n) w = n;
	if (h >= n) h = n;
	if (m + w <= n && m + h <= n) h = w = 0, m = n;
	
	H = max(h + m, n), W = max(m + w, n);
	int w1 = w, w2 = min(w + m, n), w3 = max(w + m, n);
	int n1 = w1, n2 = w2 - w1, n3 = w3 - w2;
	f[0][0][0][0][0] = f[0][0][0][0][1] = 1;
	for (int i = 0; i < H; ++i)
	{
		for (int x = 0; x <= n1; ++x)
		if (x <= k)
			for (int y = 0; y <= n2; ++y)
			if (x + y <= k)
				for (int z = 0; z <= n3; ++z)
				if (x + y + z <= k)
				{
					f[i + 1][x][y][z] = f[i][x][y][z] + f[i + 1][x][y][z];
					if(check(w1, i + 1)) f[i + 1][x + 1][y][z] = f[i + 1][x + 1][y][z] + (f[i][x][y][z] * (n1 - x));
					if(check(w2, i + 1)) f[i + 1][x][y + 1][z] = f[i + 1][x][y + 1][z] + (f[i][x][y][z] * (n2 - y));
					if(check(w3, i + 1)) f[i + 1][x][y][z + 1] = f[i + 1][x][y][z + 1] + (f[i][x][y][z] * (n3 - z));
				}
	}
	for (int x = 0; x <= n1; ++x)
		for (int y = 0; y <= n2; ++y)
			for (int z = 0; z <= n3; ++z)
			if (x + y + z == k)
			{
				ans = ans + f[H][x][y][z];
			}
			
	ans.print();
    return 0;
}