重谈主定理（master定理）及其证明
参考文章：
李卿. 递归算法分析中主定理的应用[J]. 黑龙江科技信息, 2011(29):97+207.
Thomas H.Cormen,Charles E.Leiserson,Ronald L.Rivest,Clifford Stein. 殷建平等译. 算法导论第三版 [M]. 北京:机械工业出版社,2013,55-58.
前言：
本篇文章与我的 博客园 同步更新。
在此之前，请先阅读 【洛谷日报#33】时空复杂度分析及master定理，其中关于时间复杂度表示的基础知识不再阐述。
引出：
现在考虑一个问题：假设某算法的计算时间表示为递归式：
求该算法的时间复杂度。
当给你抛出这么一个题型时，你怎么办？
凭经验和感觉蒙
小几率能蒙对，但你觉得这种题CCF会送你分吗？
递归进去
像这样递归进去:
每项都 \(n\div 2\)，总共递归 \(\log_2 n\) 层：
即 \(T(n)=\Theta(n\log^2 n)\)。
这么做不是没有道理，但是如果 \(T(n)=3T(\frac{n}{4})+n\log n\)，用这种方法根本算不出来（或许可以算出来，但是操作极其麻烦）。
主定理（master定理）求解
主定理：\(a,b\) 是常数，\(f(n)\) 为额外附加值函数\(T(n)\) 为递归式 \(T(n)=aT(\frac{n}{b})+f(n)\quad(a>0,b>1)\)，就有：
- 当 \(f(n)=\mathcal{O}(n^{(\log_ba)-\epsilon})\) 其中 \(\epsilon>0\) 是一个常数（相当于 \(\log_ba>f(n)\)），则有 \(T(n)=\Theta(n^{\log_ba})\)；
- 当 \(f(n)=\Theta(n^{\log_ba})\)，则有 \(T(n)=\Theta(n^{\log_ba}\log n)\)；
- 当 \(f(n)=\Omega(n^{(\log_ba)+\epsilon})\) 其中 \(\epsilon>0\) 是一个常数（相当于 \(\log_ba<f(n)\)），且对于一个常数 \(c<1\) 和所有足够大的 \(n\) 有 \(af(\frac{n}{b})\leq cf(n)\)（这一条件在这里可以暂时忽略不看，但在证明时起到至关重要的作用），则有 \(T(n)=\Theta(f(n))\).
- 当 \(f(n)=\Theta(n^{\log_ba}\log^kn)\) 其中 \(k\geq1\) 是一个常数，则有 \(T(n)=\Theta(n^{\log_ba}\log^{k+1}n)\)；
这么看着有点枯燥乏味的样子，不利于理解，但如果丢掉定理四的话（毕竟CSP/NOIp好像真的没考过定理四，其实可以发现定理二和定理四其实是同一种，便于萌新理解就分开了），主定理的定义可以直接写成：
（图一）
也就是 \(n^{\log_ba}\) 与 \(f(n)\) 进行比较！
图一、算法导论和上面提过的论文没有提到过定理四，但是原来那篇日报（#33）有，对此我想说，洛谷日报真是太好了！导论不行！日报行！（老伏拉夫了
举例说明：
例一：\(T(n)=4T(\frac{n}{2})+n\)，此时 \(a=4,b=2,\epsilon=1\)，那么 \(\log_ba=\log_24=2,f(n)=\mathcal{O}(n^{\log_ba-\epsilon})=\mathcal{O}(n^{2-1})\)，\(f(n)\) 成立，所以 \(T(n)=\Theta(n^{\log_ba})=\Theta(n^2)\)。
例二：\(T(n)=2T(\frac{n}{2})+n\)，此时 \(a=2,b=2\)，那么 \(\log_ba=\log_22=1,f(n)=\Theta(n^{\log_ba})=\Theta(n)\)，\(f(n)\) 成立，所以 \(T(n)=\Theta(n^{\log_ba}\log n)=\Theta(n\log n)\)。
例三：\(T(n)=4T(\frac{n}{2})+n^3\)，此时 \(a=4,b=2,\epsilon=1\)，那么 \(\log_ba=\log_24=2,f(n)=\Omega(n^{\log_ba+\epsilon})=\Omega(n^{2+1})\)，对于 \(c=\frac{2}{3}\) 和够大的 \(n\)，\(\left(af(\frac{n}{b})=4(\frac{n}{2})^3=4(\frac{n^3}{8})=\frac{n^3}{2}\right)\leq \left(cf(n)=\frac{2n^3}{3}\right)\)，\(f(n)\) 成立，所以 \(T(n)=\Theta(f(n))=\Theta(n^3)\)。
例四：\(T(n)=2T(\frac{n}{2})+n\log n\)，此时 \(a=2,b=2,k=1\)，那么 \(\log_ba=\log_22=1,f(n)=\Theta(n^{\log_ba}\log^kn)=\Theta(n\log n)\)，\(f(n)\) 成立，所以 \(T(n)=\Theta(n^{\log_ba}\log^{k+1}n)=\Theta(n\log^2 n)\)。
证明：
先声明：证明又长又臭，有亿点点难理解，学有余力的 dalao 可以来康康。
俗话说得好：“欲要证明master，就先画棵递归树”：
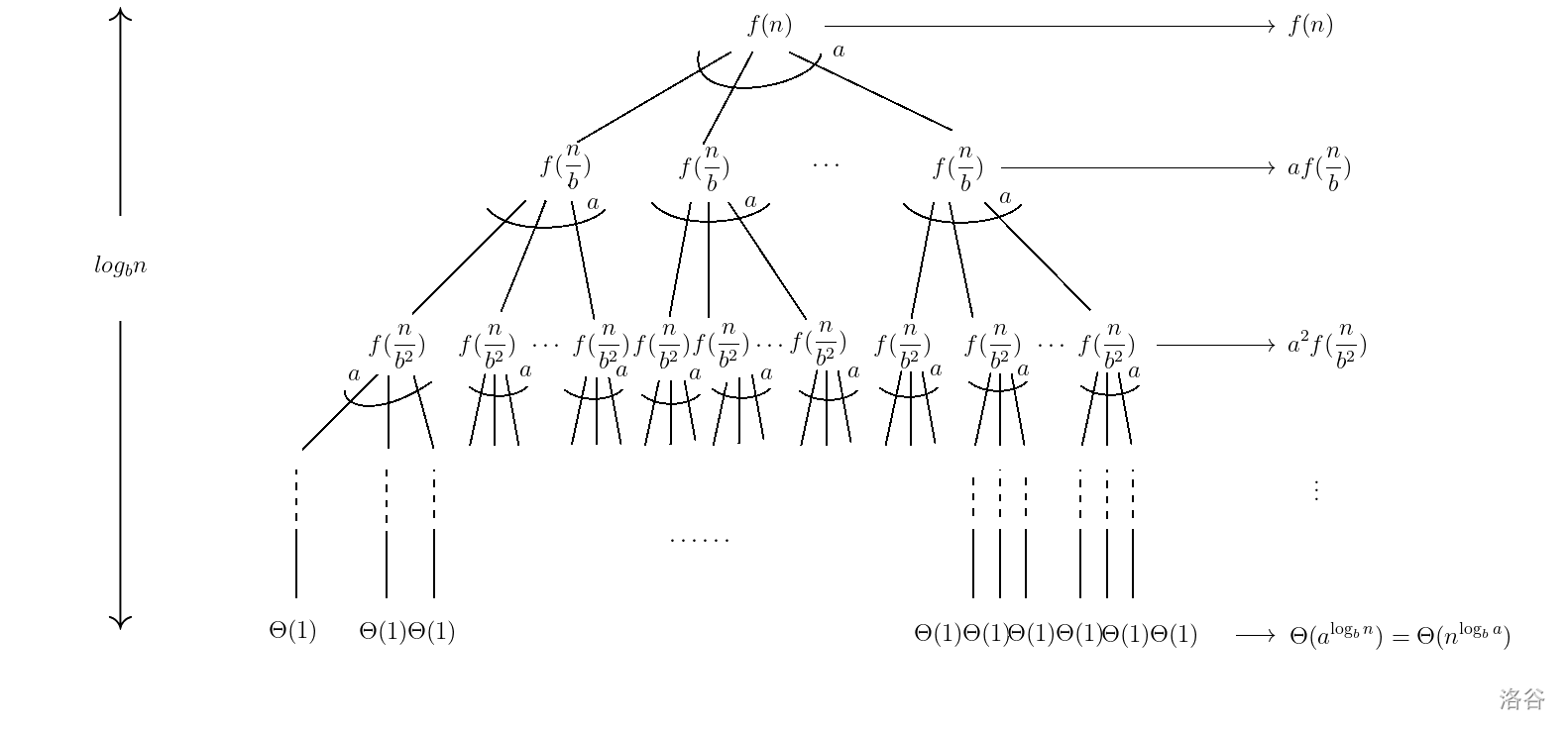
（图二）
关于图二的解释及证明：
对于第 \(i\) 层（\(i\ne \log_bn\))，有 \(a^i\) 个节点，而每个节点的值是 \(f(\frac{n}{b^i})\)，那么第 \(i\) 层总共的值是 \(a_if(\frac{n}{b^i})\)。
对于第 \(\log_bn\) 层，有 \(a^{\log_bn}\) 个节点，而每个节点的时间复杂度是 \(\Theta(1)\)，那么这一层总共的时间复杂度是 \(\Theta(a^{\log_bn})=\Theta(n^{\log_ba})\) 层。
对于 \(a^{\log_bn}=n^{\log_ba}\) 的证明：
\(a^{\log_bn}=n^{\log_ba}\) 得证。
这么看，图二的递归树的总时间复杂度为 \(T(n)=\Theta(n^{\log_ba})+\sum_{j=0}^{\log_bn-1}a^jf(\frac{n}{b^j})\)，就是叶子节点层加上其它结点层的值。
证明*：
根据上文这个 \(T(n)\) 的时间复杂度，我们定义一个函数 \(g(n)\)：
这个 \(g(n)\) 有一些性质：
- 当 \(f(n)=\mathcal{O}(n^{(\log_ba)-\epsilon})\) 其中 \(\epsilon>0\) 是一个常数，则有 \(g(n)=\mathcal{O}(n^{\log_ba})\)；
- 当 \(f(n)=\Theta(n^{\log_ba})\) 时，则有 \(g(n)=\Theta(n^{\log_ba}\log n)\)；
- 当 \(f(n)=\Omega(n^{(\log_ba)+\epsilon})\) 其中 \(\epsilon>0\) 是一个常数，且对于一个常数 \(c<1\) 和所有足够大的 \(n\) 有 \(af(\frac{n}{b})\leq cf(n)\)，则有 \(g(n)=\Theta(f(n))\).
- 当 \(f(n)=\Theta(n^{\log_ba}\log^kn)\) 其中 \(k\geq1\) 是一个常数，则有 \(g(n)=\Theta(n^{\log_ba}\log^{k+1}n)\)；
欸！有没有发现好像在哪见过！那是因为这是我从上文复制下来的（
证明关于g函数性质*：
性质 1：
将 \(f(n)=\mathcal{O}(n^{(\log_ba)-\epsilon})\) 代入进 \(g(n)=\sum_{j=0}^{\log_bn-1}a^jf(\frac{n}{b^j})\)：
然后根据等比数列求和公式化简 \(\sum_{j=0}^{\log_bn-1}(b^\epsilon)^j\)：
这里回想一下 \(b,\epsilon\) 的定义，（做到不忘初心牢记使命），它们是常数，所以式子中 \(\frac{1}{b^{\epsilon}-1}\) 也是常数，应忽略：
性质 1 得证。
性质 2：
性质 1 和性质 2 操作一样，就是一直代入再一直化简，将 \(f(n)=\Theta(n^{\log_ba})\) 代入进 \(g(n)=\sum_{j=0}^{\log_bn-1}a^jf(\frac{n}{b^j})\)：
注意：这里重头戏来了！式子中的 \(\log_bn\) 是可以直接改底数的，因为可以通过换底公式得到对数函数都是同级的。因此我们可以把 \(b\) 改成 \(2\)（即 \(\log_bn\) 化成 \(\log n\)）：
性质 2 得证。
性质 3：
性质 3 是最特殊的，用 \(af(\frac{n}{b})\leq cf(n)\) 递归 \(j\) 次可以得到 \(a^j f(\frac{n}{b^j})\leq c^j f(n)\)。再用这个式子套 \(g(n)\) 定义：
解释一下上面的式子，因为 \(c\) 都是正数，所以如果 \(g(n)\leq f(n)\sum_{j=0}^{\log_bn-1}c^j\)，显然 \(g(n)\leq f(n)\sum_{j=0}^{\infty}c^j\)。而这么做是为了更好证明。
接下来还是用等比数列求和公式化简：
你可能好奇这个等比数列求和是怎么化的，下面证明一下：
设 \(S=c^0+c^1+c^2+\cdots+c^{\infty}\) 表示 \(\sum_{j=0}^{\infty}c^j\)，此时公比为 \(c\)：
\(cS=c^1+c^2+c^3+\cdots+c^{\infty}\)，这里 \(\infty+1=\infty\)。
\((1-c)S=c^0=1\)
\(S=\frac{1}{1-c}\)
即 \(\sum_{j=0}^{\infty}c^j=\frac{1}{1-c}\)。
回到题目，由 \(g(n)\leq\left(\frac{1}{1-c}\right)f(n)\) 得到 \(g(n)=\mathcal{O}(f(n))\)。
而根据 \(g(n)\) 的定义 \(g(n)=f(n)+af(\frac{n}{b})+a^2f(\frac{n}{b^2})+\cdots+a^{\log_bn-1}f(\frac{n}{b^{\log_bn-1}})\geq f(n)\)，得到 \(g(n)=\Omega(f(n))\)。
所以 \(g(n)=\Theta(f(n))\)。
性质 3 得证。
性质 4：
老套路，将 \(f(n)=\Theta(n^{\log_ba}\log^kn)\) 代入进 \(g(n)=\sum_{j=0}^{\log_bn-1}a^jf(\frac{n}{b^j})\)：
和性质 2 一样： \(\log_bn\) 可以直接化为 \(\log n\)。然后 \(-n^{\log_ba}\sum_{j=0}^{\log_bn-1}\log^k b^j\) 是一个负数，在时间复杂度的表示中可以忽略，所以得到：
性质 4 得证。
主定理总时间复杂度证明：
回到图二的总时间复杂度 \(T(n)=\Theta(n^{\log_ba})+\sum_{j=0}^{\log_bn-1}a^jf(\frac{n}{b^j})\)。
当 \(f(n)=\mathcal{O}(n^{(\log_ba)-\epsilon})\) 时：
当 \(f(n)=\Theta(n^{\log_ba})\) 时：
当 \(f(n)=\Omega(n^{(\log_ba)+\epsilon})\)，且对于一个常数 \(c<1\) 和所有足够大的 \(n\) 有 \(af(\frac{n}{b})\leq cf(n)\)：
当 \(f(n)=\Theta(n^{\log_ba}\log^kn)\) 时：
主定理证毕。
后记 & 感谢名单：
在这篇文章证明的主定理只是对于 \(b\) 的幂下的，就是说向上、向下取整的没有证明，但要证明这些实在太难了，要花费更长的时间 （主要还是懒。
我在查找资料的时候发现还有一种定理——Akra-Bazzi定理（打开要梯子）也是时间复杂度的。
