【Luogu P2598】 [ZJOI2009]狼和羊的故事

题目大意：

给定一个 \(N\times M\) 的矩阵，矩阵上每一个点可能是狼、空地或者羊，你要在某些点的某几个边界方篱笆使得任意狼、羊不能互通。

正文：

由于每一个单位的篱笆把两个相邻的点分开，想到用最小割，原点向羊连一条无穷大的边，羊向空地和狼连一条边权为一的边，空地向其它空地和狼连边权为一的边，狼向汇点连一条无穷大的边。

如：

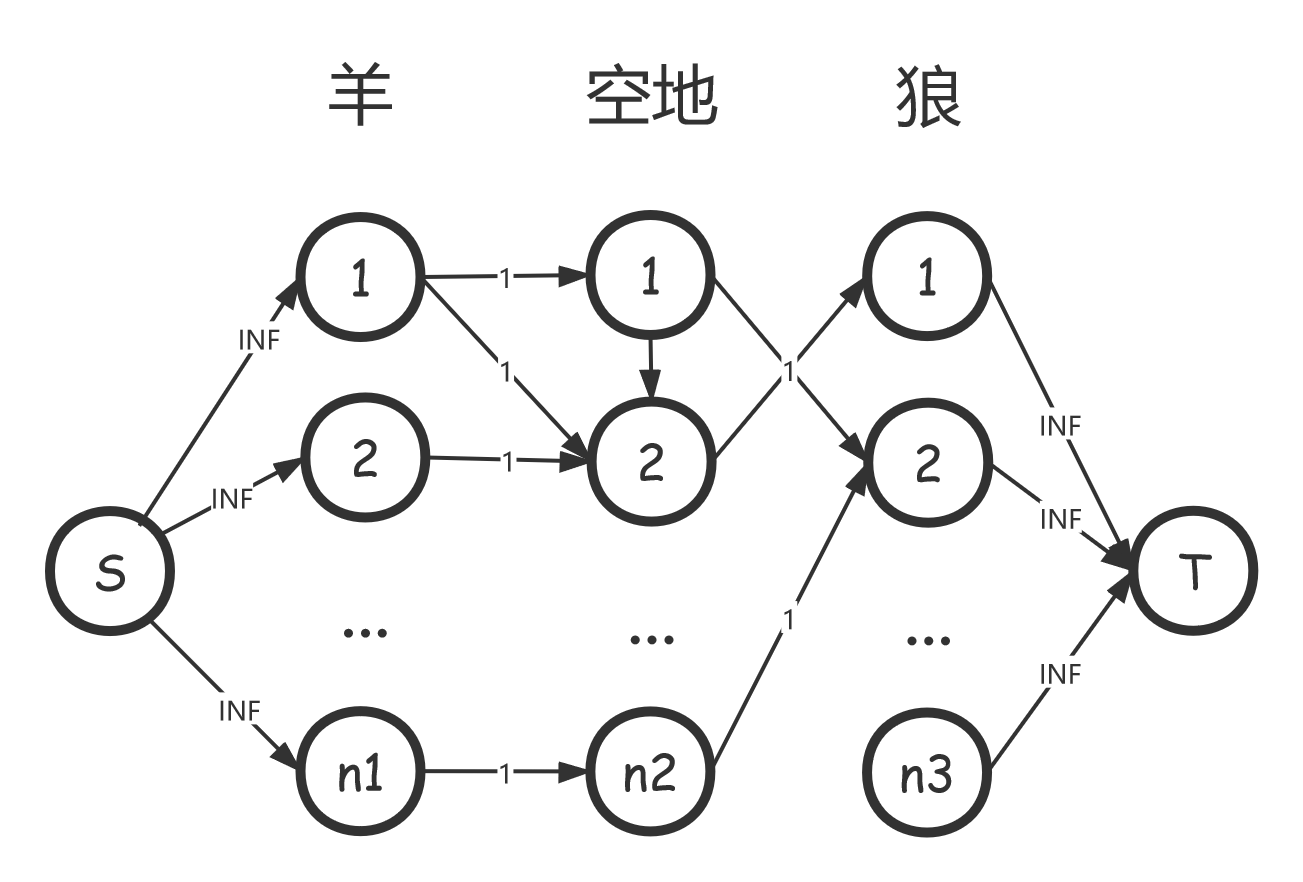
代码：

void Add(int x, int y, int w)
{
	e[++tot] = (edge){y, w, tot + 1, head[x]}; 
	head[x] = tot;
	e[++tot] = (edge){x, 0, tot - 1, head[y]}; 
	head[y] = tot; 
}

int dis[N * N];
queue <int> que;

bool bfs()
{
	while(!que.empty())que.pop();
	memset(dis, 60, sizeof(dis));
	dis[s] = 0;
	que.push(s);
	while(!que.empty())
	{
		int x = que.front();que.pop();
		for (int i = head[x]; i; i = e[i].next)
		{
			int y = e[i].y;
			if(dis[y] >= dis[x] + 1 && e[i].w)
			{
				dis[y] = dis[x] + 1;
				if(y == t) return 1;
				que.push(y);
			}
		}
	}
	return 0;
}

ll dfs(int x, ll f)
{
	if(x == t) return f;
	ll sum = 0;
	for (int i = head[x]; i; i = e[i].next)
	{
		int y = e[i].y;
		if(dis[y] == dis[x] + 1 && e[i].w)
		{
			ll f2 = dfs(y, min(e[i].w * 1ll, f - sum));
			if (!f2) dis[y] = -1;
            e[i].w -= f2; 
            e[e[i].op].w += f2;
            sum += f2;
            if (sum == f) break;
		}
	}
	return sum;
}

ll dinic()
{
	ll sum = 0;
	while(bfs()){sum += dfs(s, 1010580540);}
	return sum;
}

int main()
{
	scanf("%d%d", &n, &m);
	s = n * m + 1, t = n * m + 2; 
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			scanf ("%d", &a[i][j]);
			if(a[i][j] == 1)
			{
				Add(s, (i - 1) * m + j, 1010580540);
			} else
			if(a[i][j] == 2)
			{
				Add((i - 1) * m + j, t, 1010580540);
			}
		}
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if(a[i][j] == 1 || a[i][j] == 0)
				for (int k = 0; k < 4; k++)
				{
					int x = i + dx[k], y = j + dy[k];
					if(x <= 0 || x > n || y <= 0 || y > m)
						continue;
					if(a[x][y] == 2 || a[x][y] == 0)
						Add((i - 1) * m + j, (x - 1) * m + y, 1);
				}
		}
	printf("%lld", dinic());
	return 0;
}