【SSL 1481】 最大前缀和

题目大意：

一段长 \(n+m\) 的序列，其中 \(n\) 个是 1，\(m\) 个是 0。对序列排列求它所有前缀和的最大值的和。

正文：

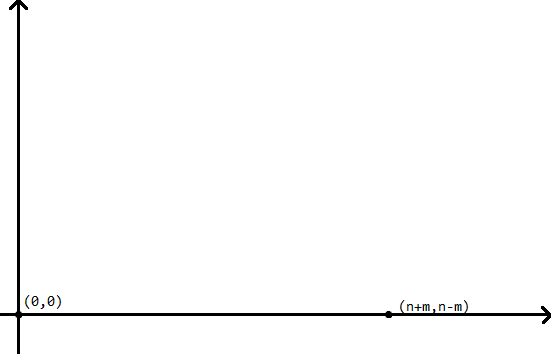
如图，其实我们就是要从点 \((0,0)\) 到点 \((n+m,n-m)\)，\(x\) 轴为走的步数，\(y\) 轴为最大前缀和。假设我们强制到 \(y\) 轴的 \(y_2\)，设 \(y_1\) 为终点即 \(n-m\)：

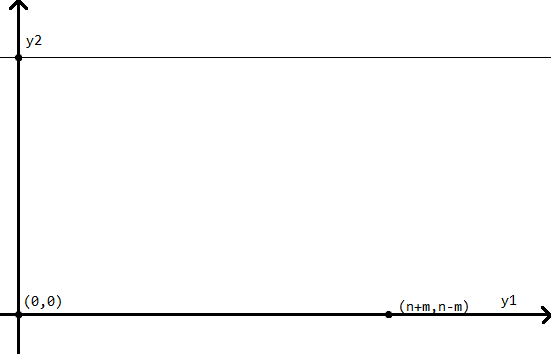
经过 \(y_2\) 的总方案为 \(C_{n+m}^{(n+m)-(y_2-y_1)}\)，运用前缀和思想，那只经过 \(y_2\) 不经过 \(y_2+1\) 的方案数就是\(y_2 + 1\) 的减去 \(y_2\) 的。

代码：

ll pow(ll a, int b)
{
    a %= p;
	ll ans = 1;
	for(; b; b >>= 1, a = a * a % p)
		if(b & 1)
			ans = ans * a % p;
    return ans;
}

inline void _init(int n, int m)
{
	prod[0] = inv[1] = 1;
	for (register int i = 1; i <= m; i++)
		prod[i] = (prod[i - 1] * i) % p;
	inv[n + m] = pow(prod[n + m], p - 2);
	for (register int i = n + m - 1; i > 1; --i)
		inv[i] = inv[i + 1] * (i + 1) % p;
}

inline ll C(ll n,ll m){
    if(m > n)return 0;
    return (prod[n]*inv[m] % p * inv[n - m] % p);
}

int main()
{
	scanf ("%lld%lld", &n, &m);
	_init(0, n + m);
	ll pre = 1;
	ans = n;
	for (register int i = n - 1; i >= n - m; --i)
	{
		ll s = (C(n + m, (n - i) % p) - pre + p) % p;
		pre = (s + pre) % p;
		if(i > 0) ans = (ans + s * i % p) % p;
		else break;
	}
	printf("%lld", ans);
	return 0;
}