【Luogu P6374】 「StOI-1」树上询问

错误修改：

upd:2020/8/22 :举例说明时数据列错了

题目大意：

给定一棵 \(n\) 个点的无根树，有 \(q\) 次询问。每次询问给一个参数三元组 \((a,b,c)\)，求有多少个 \(i\) 满足这棵树在以 \(i\) 为根的情况下 \(a\) 和 \(b\) 的 LCA 为 \(c\) 。

正文：

要解决此题，首先得找到一些规律。

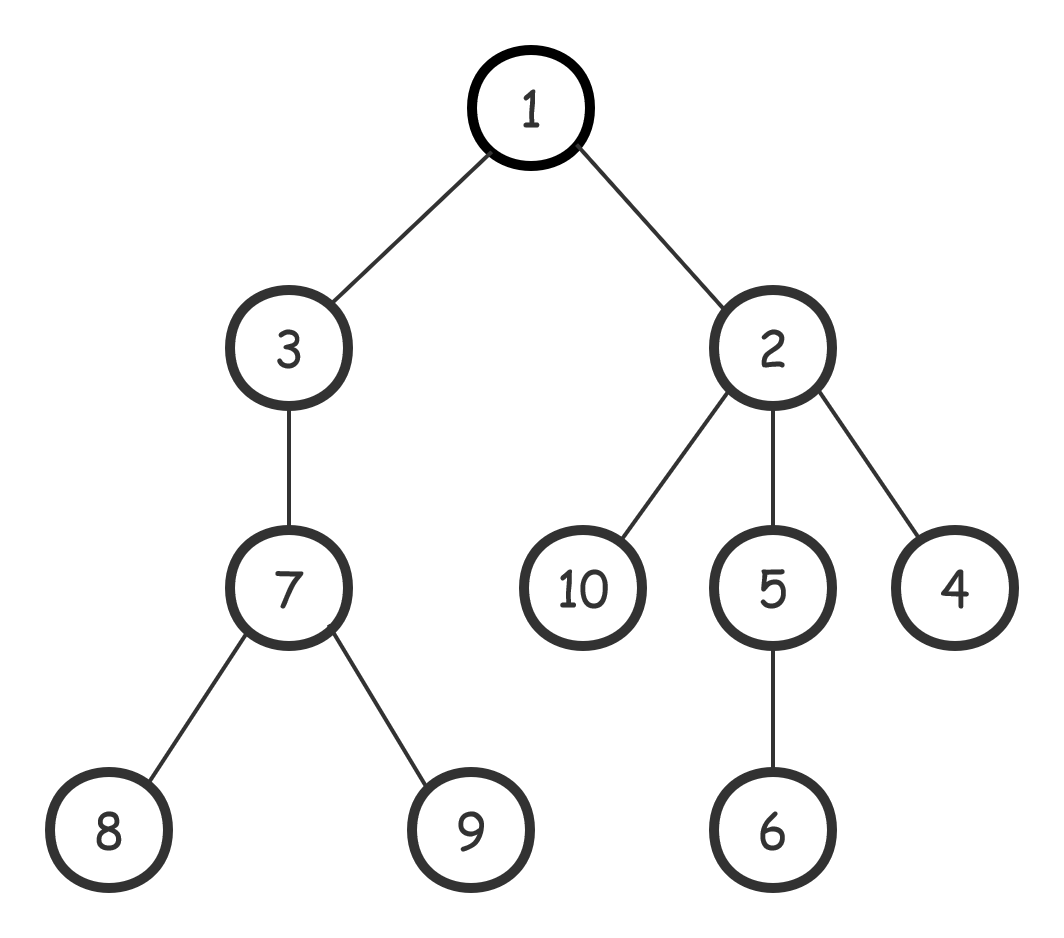
我们拿样例的图来找到它们。

假设三元组是 \((10,6,2)\) 时，即 \(c\) 是 \(a,b\) 的 LCA，那么有多少个节点能成为根节点呢？可以发现有 \(7\) 个（分别是 \(1,2,3,4,7,8,9\)）节点，就是当 \(c\) 为根节点时，除了 \(a,b\) 所在子树的节点，其它节点都可成为根节点。

假设三元组是 \((5,7,2)\) 时，即 \(c\) 在 \(a\) 通往 \(a,b\) 的 LCA 的 道路上，有 \(3\) 个（是 \(10,2,4\)），就是以 \(c\) 为根的子树的节点数量减去 \(a\) 所在子树的节点数量。如果 \(c\) 在 \(b\) 通往 \(a,b\) 的 LCA 的 道路上则反之。

若 \(c\) 不在任意一点 通往 \(a,b\) 的 LCA 道路上时，如 \((3,2,7)\)，明显无解。

代码：

void dfs (int x, int fa)
{
	size[x] = 1; 
	for (int i = head[x]; i; i = next[i])
	{
		int y = to[i];
		if (y == fa) continue;
		dfs(y, x);
		size[x] += size[y];
	}
} 

void bfs (int root)
{
	q.push(root); d[root] = 1;
	while (!q.empty())
	{
		int x = q.front(); 
		q.pop();
		for (int i = head[x]; i; i = next[i])
		{
			int y = to[i];
			if (d[y]) continue;
			d[y] = d[x] + 1;
			f[y][0] = x;
			for (int j = 1; j <= num; j++)
				f[y][j] = f[f[y][j - 1]][j - 1];
			q.push(y);
		}
	} 
} 

int lca (int x, int y)
{
	if (d[x] > d[y])
	{
		int t = x;
		x = y;
		y = t;
	}
	for (int i = num; i >= 0; i--)
		if (d[f[y][i]] >= d[x])
			y = f[y][i];
	if (x == y) return x;
	for (int i = num; i >= 0; i--)
		if (f[x][i] != f[y][i])
		{
			x = f[x][i];
			y = f[y][i];
		}
	return f[x][0];
}

bool check (int x, int y, int z)         //是否在道路上 
{
	int k = lca(x, z);
	return ((lca(x, y) == y) || (lca(y, z) == y)) && lca(y, k) == k;
}

int Val (int x, int y)          //求a（b）所在子树大小 
{
	if (x==y) return 0;
	for (int i = num; i >= 0; i--)
		if(d[f[x][i]] > d[y])
			x = f[x][i];
	return size[x];
}

int main()
{
	scanf ("%d%d", &n, &m); num = (int) (log2(n)) + 1;
	for (int i = 1; i < n; i++)
	{
		int x, y;
		scanf ("%d%d", &x, &y);
		add(x, y), add(y, x);
	}
	dfs (1, 0);
	bfs (1);
	for (; m--;)
	{
		int x, y, z;
		scanf ("%d%d%d", &x, &y, &z);
		int v = lca(x, y);
		if(v == z) printf("%d\n", n - Val(x, v) - Val(y, v));
		else if(check(x, z, v)) printf("%d\n", size[z] - Val(x, z));
			else if(check(y, z, v)) printf("%d\n", size[z] - Val(y, z));
				else puts("0");
	}
	return 0;
}