【Luogu P2508】 [HAOI2008]圆上的整点

题目大意：

求一个给定的圆 \((x^2+y^2=r^2)\)，在圆周上有多少个点的坐标是整数。

正文：

声明： 此方法概括（转）自 3b1b 的视频。

如果我们直接照着题目给出的勾股定理枚举，最优解的时间复杂度似乎就只有 \(O(r)\)，可 \(r\) 达到二十亿，这方法觉得行不通。

数学里比较常见的是，当你看到和二维平面有关的问题时，就把这个平面看成全体复数的集合，再看问题或许会有意外收获
——3blue1brown

up主给我的启示很有用。当在半径是 \(5\) 的圆周上，有一个整点的坐标是 \((x,y)\)，那么将二维平面转换成复平面，那个整点也跟着转换成一个复数 \(Z=x+yi\)。

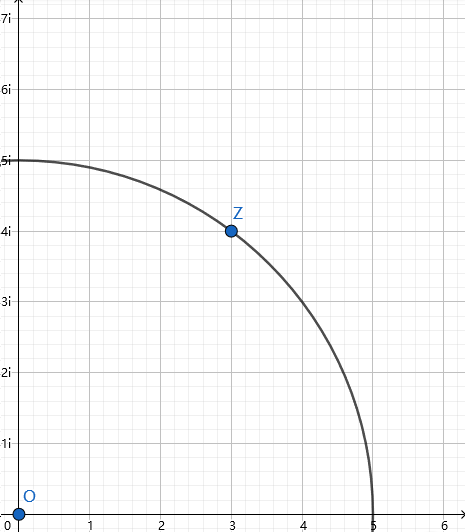
（图中 \(Z=3+4i\)）

那么半径 \(\begin{aligned}r & = \overrightarrow{AB} \\ & = \sqrt{x^2+y^2} \\ & = (x+yi)(x-yi)\end{aligned}\)。这样问题就可以转为分解质因数。

而所有满足这样的整数就是高斯整数。问题就是求有多少个高斯整数能满足其自身与其复共轭的积是圆的半径。我们可以通过分解质因数的方式求出高斯整数的数目。如质数 \(5\)，它能分解成一个高斯整数 \((2+i)\)。但只有模四余一的质数才会对答案有贡献，如质数 \(7\)，不能分解质数。

代码：

int main()
{
	scanf ("%lld", &r);
	prime(100000);
	for (int i = 1; i <= cnt; i++)
	{
		int num = 0;
		for (; r % pri[i] == 0;r/=pri[i],num++);
		if (pri[i] % 4 == 1) ans *= num * 2 + 1ll;  //每个质数的贡献，乘2是因为视频里是根号r，这里是r，质因数翻倍
	}
	if(r > 1 && r % 4 == 1)ans *= 3;  //当半径模四余一的特例
	printf("%lld", ans * 4ll); //复数及其复共轭皆可乘虚数i，一共四种
	return 0;
}