【SSL2325】最小转弯问题

题面:

\[\Large\text{最小转弯问题} \]

\[Time~Limit:1000MS~~Memory~Limit:65536K \]

Description

给出一张地图，这张地图被分为 n×m（n,m<=100）个方块，任何一个方块不是平地就是高山。平地可以通过，高山则不能。现在你处在地图的（x1,y1）这块平地，问：你至少需要拐几个弯才能到达目的地（x2,y2）？你只能沿着水平和垂直方向的平地上行进，拐弯次数就等于行进方向的改变（从水平到垂直或从垂直到水平）的次数。例如：如图 1，最少的拐弯次数为5。

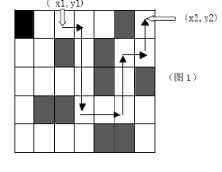
Input

第 1行：n m 第 2至n+1行：整个地图地形描述（0：空地；1：高山）， 如图,第2行地形描述为：1 0 0 0 0 1 0 第3行地形描述为：0 0 1 0 1 0 0 …… 第n+2行：x1 y1 x2 y2 （分别为起点、终点坐标）

Output

s （即最少的拐弯次数

Sample Input

5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0  
0 0 0 0 1 0 1  
0 1 1 0 0 0 0  
0 0 0 0 1 1 0 
1 3 1 7 

Sample Output

5

正文：

方法1

对于某个点，可以先搜出不拐弯的点（即四个方向一直延伸，搜到不能再搜），搜到终点直接输出，这样就能保证终点是最小拐弯的。

方法2（一个想法，未证实）

\(\because\) 显然的 两点之间直线最短

\(\therefore\) 我们可以逆向思考，通过最短路径求出最小拐弯。

但是！会有一个锅，当图是这个时：

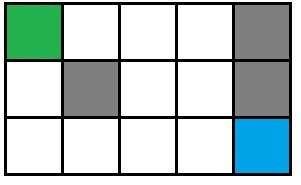
（绿点是起点，蓝点是终点）

程序可能会这么走：

但应该这么走：

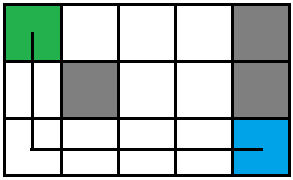
路径都是\(6\)，但是拐弯数不同。所以我们不能搜到终点就直接输出，判重时，如果走过的路径长度和现在走到的路径长度就让它继！续！搜！（但是如果转弯次数更多可以剪个枝）最后再输出。