【JZOJ 3490】旅游
题目
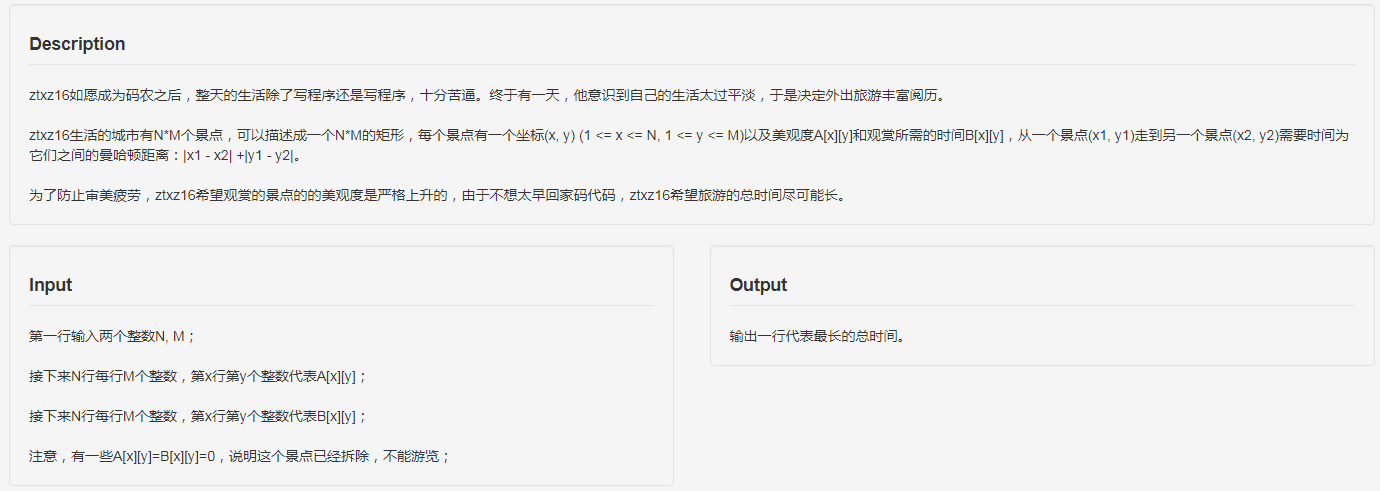
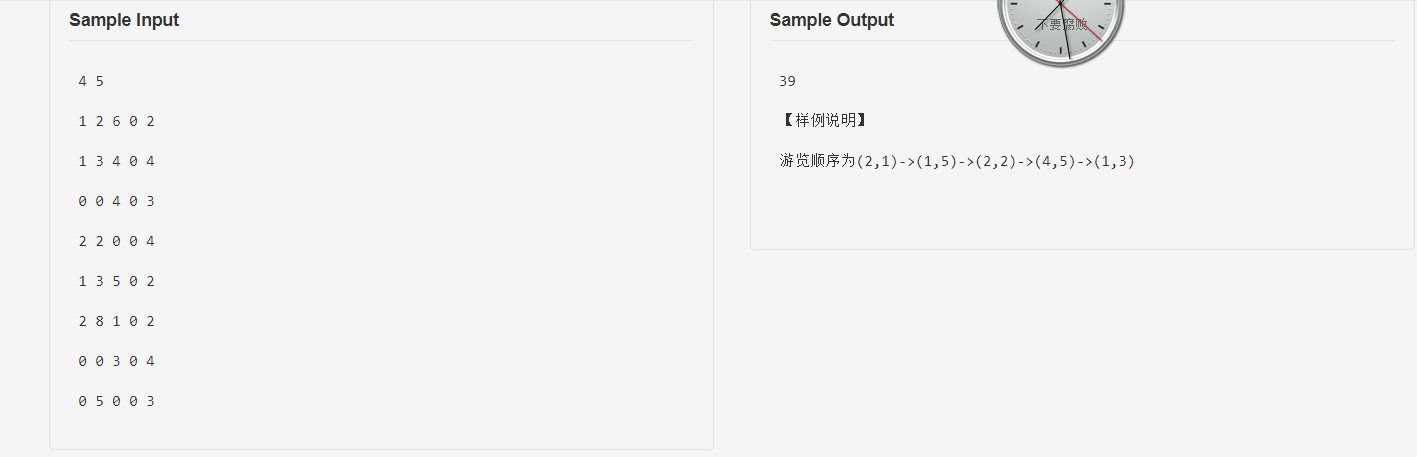
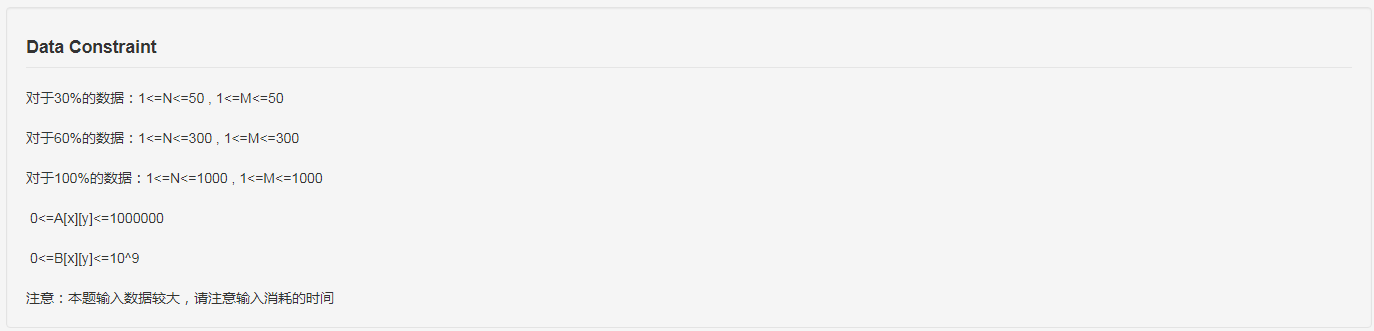
思路
这道题看上去就像一个动态规划!但是还是要把矩阵压成一行。
然后按 \(A\)数组 将结构体从小到大排个序。
随后我们开始了动规标准步骤:
确定状态
很显然, \(f_i\) 表示游览完第\(~i~\)个景点是的最长时间。
Q(动规小白为啥动规小白要做这题啊):怎么看粗来的???
A:动规不是一维不行加一维的吗
确定转移方程
有了这个状态相信动规小白也能看粗来转移方程吧!
那么我们假设看完了第\(j\)个景点后就去了第\(i\)个景点(\(j~ \rightarrow ~i\))。
那么我们的方程就显而易见了。
\[\begin{matrix}f_i = max\{ f_j + (| ~ x_i - x_j ~ | + | ~ y_i-y_j ~ |) \}+B_i\\ =max\{ f_j + dis(i, j)\}+B_i~~~~~~~~~~~~~~~~~~~~\end{matrix}
\]
温馨提示:
可以发现直接暴力这么做的时间复杂度是\(O((nm)^2)\)
即使我们的题目限时两秒也会炸!!!
Q:怎么办呢???
卡常!!!
1、
如果\(j\)直接从\(1\)开始枚举就会有冗余的情况:
假设你的\(A_i\)是\(4\)。
\(A_{1 \sim i-1}\)分别是\(\{ 1,1,1,1,1,2,2,2,3 \}\)。
你肯定选\(3\)都要比选其他的数要强(请读者自行理解),所以从\(3\)的那里开始
2、
使用
register
SPFA
是的又是很明显地就可以看出,这题可以用最短路。
存邻接表时就只存比第\(i\)个小的就行了,剩下的就是SPFA模板了
最后
关于SPFA
- 它死了


