20162323周楠 2017-2018-1 《程序设计与数据结构》实验报告二

20162323周楠 2017-2018-1 《程序设计与数据结构》实验报告二

目录预览

• 实验二 树-1-实现二叉树
• 实验二 树-2-中序先序序列构造二叉树
• 实验二 树-3-决策树
• 实验二 树-4-表达式树
• 实验二 树-5-二叉查找树
• 实验二 树-6-红黑树分析
• 资料参考
• 代码托管

实验二 树-1-实现二叉树

---

实现二叉树

实验结果

实验过程

先补全书上缺少的那部分代码

public LinkedBinaryTree<T> getRight() throws EmptyCollectionException {
        if (root == null)
            throw new EmptyCollectionException ("Get left operation "
                    + "failed. The tree is empty.");

        LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
        result.root = root.getRight();

        return result;
    }

    public boolean Contains (T target) {
        BTNode<T> node = null;

        if (root != null)
            node = root.find(target);

        if (node == null)
            return false;

        else
            return true;
    }

    public boolean isEmpty() {
        return (size() == 0);
    }

    public String toString() {
        String result = "";
        ArrayIterator<T> iter = null;
        try {
            iter = (ArrayIterator<T>) levelorder();
        }
        catch (EmptyCollectionException e) {
        }
        result = iter.toString();
        return result;
    }

    public Iterator<T> preorder() {
        ArrayIterator<T> iter = new ArrayIterator<T>();

        if (root != null)
            root.preorder (iter);

        return iter;
    }

    public Iterator<T> postorder() {
        ArrayIterator<T> iter = new ArrayIterator<T>();

        if (root != null)
            root.postorder (iter);

        return iter;
    }

    public
    void CreateTree(String[] inorder, String[] preoder) {

    }
}

用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试

package javafoundations;

import junit.framework.TestCase;

public
class LinkedBinaryTreeTest extends TestCase {
    private LinkedBinaryTree<String> tree;

    public LinkedBinaryTreeTest() {

        String a1 = "What's your name?";
        String a2 = "What's your last name?";
        String a3 = "What's your first name?";
        String a4 = "ZHOU";
        String a5 = "WANG";
        String a6 = "NAN";
        String a7 = "YU";

        LinkedBinaryTree <String> n2, n3, n4, n5, n6, n7;

        n4 = new LinkedBinaryTree <String>(a4);
        n5 = new LinkedBinaryTree <String>(a5);
        n2 = new LinkedBinaryTree <String>(a2,n4,n5);
        n6 = new LinkedBinaryTree <String>(a6);
        n7 = new LinkedBinaryTree <String>(a7);
        n3 = new LinkedBinaryTree <String>(a3,n6,n7);

        tree = new LinkedBinaryTree <String>(a1,n2,n3);

    }
    public
    LinkedBinaryTreeTest(LinkedBinaryTree <String> tree) {
        this.tree = tree;
    }

    public
    void testGetRight() throws Exception, EmptyCollectionException {
        assertEquals("What's your first name?","[What's your first name?, NAN, YU]",tree.getRight().toString());
    }

    public
    void testContains() throws Exception {
        assertEquals(true, tree.Contains("What's your first name?"));
    }

    public
    void testToString() throws Exception, EmptyCollectionException {
        assertEquals("What's your name?, What's your last name?, " +
                "What's your first name?, ZHOU, WANG, NAN, " +
                "YU","[What's your name?, What's your last name?, Wh" +
                "at's your first name?, ZHOU, WANG, NAN, YU]",tree.levelorder().toString() );
   }

    public
    void testPreorder() throws Exception,EmptyCollectionException {
        assertEquals("[]","[]",tree.preorder().toString() );
    }

---

实验二 树-2-中序先序序列构造二叉树

---

中序先序序列构造二叉树

实验结果

实验过程

BTNode root = new BTNode(pre[0]);//定义二叉树的根节点
        int i = 0;
        while(in[i] != pre[0]){//找到根节点再中序遍历里的位置，
            i++;
      

String[] preLeft = new String[i];//左子树先序遍历
        String[] inLeft = new String[i]; //左子树中序遍历
        String[] preRight = new String[pre.length - i - 1];//右子树先序遍历
        String[] inRight = new String[in.length - i - 1];//右子树中序遍历
        for(int j = 0;j<in.length;j++){
            if(j < i){
                preLeft[j] = pre[j+1];
                inLeft[j] = in[j];
            }else if(j > i){
                preRight[j-i-1] = pre[j];
                inRight[j-i-1] = in[j];
            }
        }
        root.left = ConstructBinaryTree(preLeft,inLeft);//递归构建左子树
        root.right = ConstructBinaryTree(preRight,inRight);//递归构建右子树
        return root;//返回重新构建二叉树

public static void last(BTNode tree){//后序遍历遍历二叉树
        if(tree == null){
            return ;
        }
        last(tree.getLeft());
        last(tree.getRight());
        System.out.print(tree.element+" ");
 ![](http://images2017.cnblogs.com/blog/1062821/201710/1062821-20171029232804523-1108288208.png)

   }
    public static void main(String[] args) {
        String[] b = {"H","D","I","B","E","M","J","N","A","F","C","K","G","L"};
        String[] a = {"A","B","D","H","I","E","J","M","N","C","F","G","K","L"};
        BTNode root = ConstructBinaryTree(a,b);
        last(root);

---

实验二 树-3-决策树

---

决策树

实验结果

实验过程

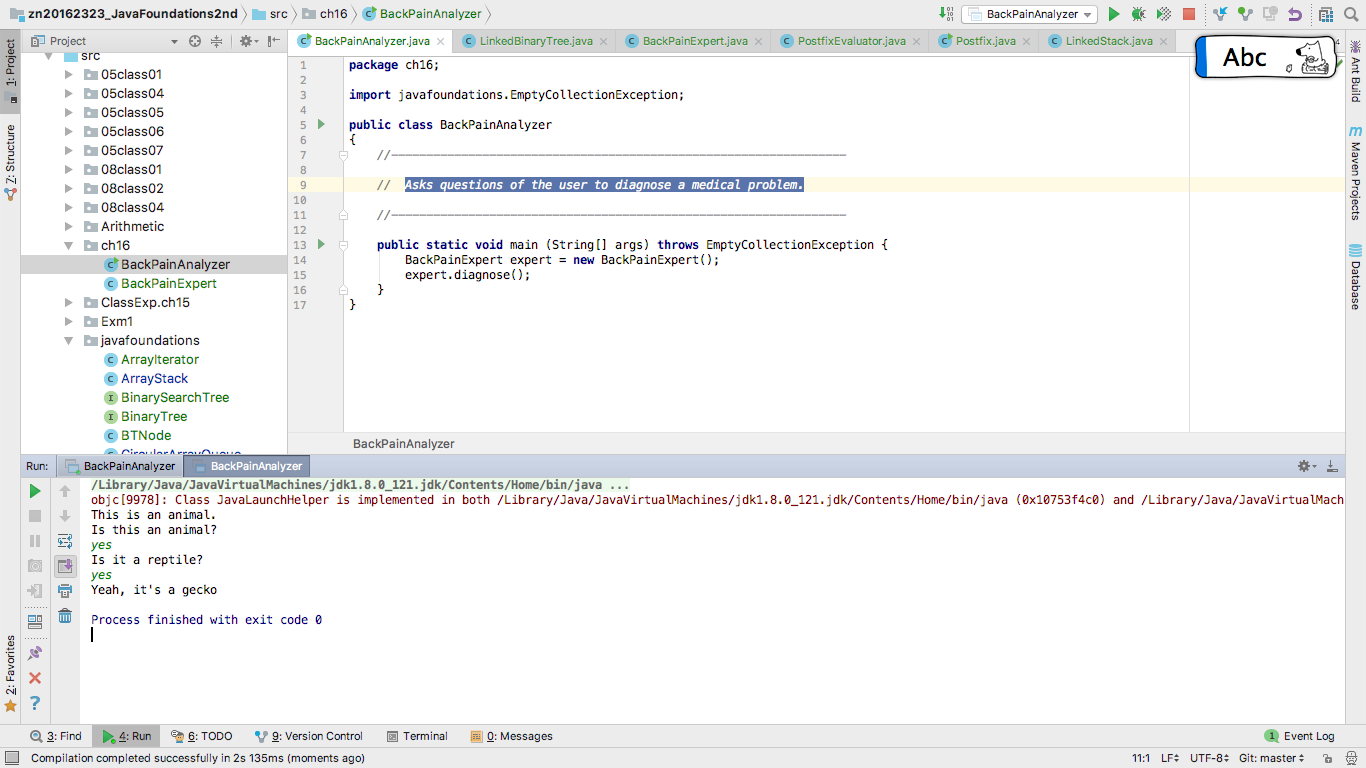
根据书上代码BackPainAnalyzer改写

package ch16;

import javafoundations.*;
import java.util.Scanner;

public class BackPainExpert
{
    private LinkedBinaryTree<String> tree;

    //-----------------------------------------------------------------
    //  Sets up the diagnosis question tree.
    //-----------------------------------------------------------------
    public BackPainExpert()
    {
        String e1 = "Is this an animal?";
        String e2 = "Is it big?";
        String e3 = "Is it a reptile?";
        String e4 = "Is it four legs?";
        String e5 = "Is it two legs?";
        String e6 = "Is it neck long?";
        String e7 = "Yeah, it's a gecko";
        String e8 = "Yeah, it's a tiger";
        String e9 = "Yeah, it's a kangaroo";
        String e10 = "Yeah, it's a kangaroo";
        String e11 = "Yeah, it's a tiger";
        String e12 = "Yeah, it's a giraffe";
        String e13 = "Yeah, it's a tiger";

        LinkedBinaryTree<String> n2, n3, n4, n5, n6, n7, n8, n9,
                n10, n11, n12, n13;

        n8 = new LinkedBinaryTree<String>(e8);
        n9 = new LinkedBinaryTree<String>(e9);
        n4 = new LinkedBinaryTree<String>(e4, n8, n9);

        n10 = new LinkedBinaryTree<String>(e10);
        n11 = new LinkedBinaryTree<String>(e11);
        n5 = new LinkedBinaryTree<String>(e5, n10, n11);

        n12 = new LinkedBinaryTree<String>(e12);
        n13 = new LinkedBinaryTree<String>(e13);
        n6 = new LinkedBinaryTree<String>(e6, n12, n13);

        n7 = new LinkedBinaryTree<String>(e7);

        n2 = new LinkedBinaryTree<String>(e2, n4, n5);
        n3 = new LinkedBinaryTree<String>(e3, n6, n7);

        tree = new LinkedBinaryTree<String>(e1, n2, n3);
    }

    //-----------------------------------------------------------------
    //  Follows the diagnosis tree based on user responses.
    //-----------------------------------------------------------------
    public void diagnose() throws EmptyCollectionException {
        Scanner scan = new Scanner(System.in);
        LinkedBinaryTree<String> current = tree;

        System.out.println ("This is an animal.");
        while (current.size() > 1)
        {
            System.out.println (current.getRootElement());
            if (scan.nextLine().equalsIgnoreCase("N"))
                current = current.getLeft();
            else
                current = (LinkedBinaryTree <String>) current.getRight();
        }

        System.out.println (current.getRootElement());
    }
}

---

实验一 线性结构-4

---

表达式树

实验结果

---

实验二 树-5-二叉查找树

*** ### 二叉查找树 

实验结果

实验过程

package javafoundations;

import junit.framework.TestCase;

public
class LinkedBinarySearchTreeTest extends TestCase {
    LinkedBinarySearchTree tree = new LinkedBinarySearchTree<Integer>();


    public
    void testFindMin() throws Exception, ElementNotFoundException {
        tree.add("1");
        tree.add("2");
        tree.add("3");
        tree.add("5");
        tree.add("6");

        assertEquals("1","1",tree.findMin().toString());

    }

    public
    void testFindMax() throws Exception {
        tree.add("1");
        tree.add("2");
        tree.add("3");
        tree.add("5");
        tree.add("6");

        assertEquals("6","6",tree.findMax().toString());

    }

}

补充书上代码

  public T findMin() {
         T min = null;
         while (root.getLeft()!=null ){
             root = root.getLeft();

         }
         min = root.getElement();
         return min;
     }
     public T findMax() {
         T max = null;
         while (root.getRight()!=null ){
             root = root.getRight();

         }
         max = root.getElement();
         return max;
     }

实验二 树-6-红黑树分析

***

红黑树分析

实验过程

• 红黑树的时间复杂度为: O(lgn)

红黑树的基本操作

红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后，都会用到旋转方法。

1.左旋

对x进行左旋，意味着"将x变成一个左节点"。

• 源代码

LEFT-ROTATE(T, x)  
 y ← right[x]            // 前提：这里假设x的右孩子为y。下面开始正式操作
 right[x] ← left[y]      // 将 “y的左孩子” 设为 “x的右孩子”，即 将β设为x的右孩子
 p[left[y]] ← x          // 将 “x” 设为 “y的左孩子的父亲”，即 将β的父亲设为x
 p[y] ← p[x]             // 将 “x的父亲” 设为 “y的父亲”
 if p[x] = nil[T]       
 then root[T] ← y                 // 情况1：如果 “x的父亲” 是空节点，则将y设为根节点
 else if x = left[p[x]]  
           then left[p[x]] ← y    // 情况2：如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
           else right[p[x]] ← y   // 情况3：(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
 left[y] ← x             // 将 “x” 设为 “y的左孩子”
 p[x] ← y                // 将 “x的父节点” 设为 “y”

2.右旋

• 源代码

RIGHT-ROTATE(T, y)  
  x ← left[y]             // 前提：这里假设y的左孩子为x。下面开始正式操作
  left[y] ← right[x]      // 将 “x的右孩子” 设为 “y的左孩子”，即 将β设为y的左孩子
  p[right[x]] ← y         // 将 “y” 设为 “x的右孩子的父亲”，即 将β的父亲设为y
  p[x] ← p[y]             // 将 “y的父亲” 设为 “x的父亲”
  if p[y] = nil[T]       
  then root[T] ← x                 // 情况1：如果 “y的父亲” 是空节点，则将x设为根节点
  else if y = right[p[y]]  
            then right[p[y]] ← x   // 情况2：如果 y是它父节点的右孩子，则将x设为“y的父节点的左孩子”
            else left[p[y]] ← x    // 情况3：(y是它父节点的左孩子) 将x设为“y的父节点的左孩子”
  right[x] ← y            // 将 “y” 设为 “x的右孩子”
  p[y] ← x                // 将 “y的父节点” 设为 “x”

2.添加

RB-INSERT(T, z)  
 y ← nil[T]                        // 新建节点“y”，将y设为空节点。
 x ← root[T]                       // 设“红黑树T”的根节点为“x”
 while x ≠ nil[T]                  // 找出要插入的节点“z”在二叉树T中的位置“y”
     do y ← x                      
        if key[z] < key[x]  
           then x ← left[x]  
           else x ← right[x]  
 p[z] ← y                          // 设置 “z的父亲” 为 “y”
 if y = nil[T]                     
    then root[T] ← z               // 情况1：若y是空节点，则将z设为根
    else if key[z] < key[y]        
            then left[y] ← z       // 情况2：若“z所包含的值” < “y所包含的值”，则将z设为“y的左孩子”
            else right[y] ← z      // 情况3：(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子” 
 left[z] ← nil[T]                  // z的左孩子设为空
 right[z] ← nil[T]                 // z的右孩子设为空。至此，已经完成将“节点z插入到二叉树”中了。
 color[z] ← RED                    // 将z着色为“红色”
 RB-INSERT-FIXUP(T, z)             // 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转，让树T仍然是一颗红黑树

---

资料参考

*** [红黑树](http://www.cnblogs.com/skywang12345/p/3245399.html)

---

代码托管

***

代码托管

---

PSP(Personal Software Process)时间

步骤	耗时	百分比
需求分析	40min	6%
代码实现	500min	75.8%
测试	90min	13.6%
总结	30min	4.6%

---