NOIP2024加赛8

NOIP2024加赛8

T1 flandre

第 4 个样例没给全，说明这可以直接猜结论

首先我们假设选定了 $ x $ 个数，那么我们肯定是把他们从小到大排好序依次放，这样才能使整体效果最大。然后我们考虑怎么选这些数。首先正的肯定都要，然后就是负的，然后你就猜排好序后选择的区间一定是连续的。

证明：

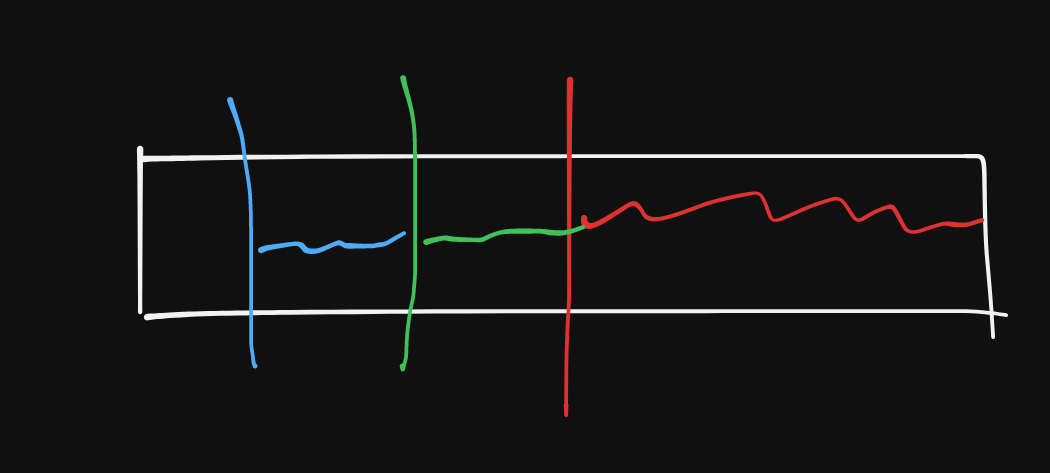
红色的是已经选的部分，绿色的是不选的部分，蓝色的是后来选择的部分，这样选的区间不是连续的与结论相反，然后我们考虑能不能把蓝色中的一个部分换成绿色中的一个部分，首先考率一个点的贡献，由 它本身的值，被前面的点加的值，和给后面点加的贡献 三部分组成，首先考虑蓝色的 $ i $ ，和绿色的 $ j $ ， 第 $ k $ 部分贡献成为 $ w_k $ ，那么 $ w_{i,1} \le w_{j,1} ， w_{i,2} \le w_{j,2} ， w_{i,3} \le w_{j,3} $ ，所以 $ j $ 一定 优于 $ i $ ，那么我们可以把所有蓝色的换成绿色的，所以答案区间必定是连续的。

然后排序就做完了。

T2 meirin

上来 4 个 $ \sum $ 直接把我吓死。

但是把式子写成人话就是对于所有的区间 $ [l,r] $ ，他的贡献是 $ \sum_{i=l}^{r} a_i \times \sum_{i=l}^{r} b_i $ ，然后我们先想想那个弱化版怎么求，其实我们直接考虑对于 $ b_i $ 哪些区间 $ [l,r] $ 有 $ b_i $ 的贡献，显然就是 $ [l,r] , l \le i , r \ge i $ ，的区间，那么 $ b_i $ 的贡献就是 $ \sum_{l=1}^{i} \sum_{r=i}^{n} \sum_{j=l}^{r} a_j = \sum_{r=i}^{n} pre_r - \sum_{l=1}^{i} pre_{l-1} $ 这个全局直接 $ O(n) $ 做就行了，原题可做了，但是带修怎么搞，其实很简单，因为一个 $ b_i \gets b_i + 1 $ ，全局的答案 $ ans \gets ans + (p_i = \sum_{r=i}^{n} pre_r - \sum_{l=1}^{i} pre_{l-1} ) $ ， 所以再给 $ p_i $ 做个前缀和然和直接 $ O(1) $ 修改、查询。其实直接线段树也能过。

T3 sakuya

直接模拟肯定 T 了，考虑怎么算贡献，我们把那个求和式展开，可以看出贡献就是由 $ d_{ a_i,a_{i+1} } $ 来的，所以我们可以直接枚举 一对点 $ x,y $ （分先后顺序） ，他们的贡献是 $ d_{ x,y } \div m $ ，所以我们现在有 $ O(qn^2) $ 做法，然后再继续拆贡献， $ d_{x,y} = dis_{x} + dis_{y} - dis_{lca(x,y)} \times 2 $ ，然后就把贡献拆到每个点身上了，开局 dfs 处理出 一个点被计算次数，然后直接算就行，改变一个点旁边的权值就直接是个区间加，直接加就行。

T4 红楼 ~ Eastern Dream

牛魔，写了个优化然后优化挂了，直接给 80 pts 覆盖了。哭（

其实是良心 T4。

首先很容易想到根号分治，但是 $ \le \sqrt n $ 的 时间复杂度是 $ \sqrt n $ 的，但是 $ \gt \sqrt n $ 的还有一个区间加，是 $ \sqrt n \log n $ 的，微调块长后可以做到 $ \sqrt{n \log n} $ 的，标算 3e8 ， 很难卡过去。然后注意到，这一块的查询和修改很不平均，查询是 $ O(\log n ) $ 的，而修改是 $ O(\sqrt{n \log n}) $ 的 。我们使用根号平衡，看看能不能 $ O(1) $ 修改， $ O(\sqrt n ) $ 查询，应该只能是差分了，那我们差分之后分块维护一些信息。具体说，查询一段区间 $ [l,r] $ 的值，相当于查询 $ \sum_{i=l}^{r} \sum_{1}^{i} c_i $ ， $ c $ 是差分数组，也就相当于查询 $ \sum_{i=1}^{l-1} c_i \times (r-l+1) + \sum_{i=l}^{r} c_i \times (r-i+1) $ ，直接分块维护 $ \sum c_i , \sum c_i \times i $ 即可。

\[\]

\[\]

\[\]

闲话：

昨天反思完之后今天考试时效率确实高了点，坏消息：最后 30 min 真正看 T3 ， 好消息： 一下就像出来正解了 ，坏消息： 最后 5 min了过了小样例和第一个大样例，好消息：最后 40 s 过了大样例 ，坏消息： 虚拟机太慢了，最后20 s 才进入网站，好消息： 交上去了，坏消息：炸空间了，一分没有。

NOIP RP++