题解:聪聪与可可(概率与期望)
[NOI2005] 聪聪与可可
题目描述
在一个魔法森林里,住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。虽然灰姑娘非常喜欢她们俩,但是,聪聪终究是一只猫,而可可终究是一只老鼠,同样不变的是,聪聪成天想着要吃掉可可。
一天,聪聪意外得到了一台非常有用的机器,据说是叫 GPS,对可可能准确的定位。有了这台机器,聪聪要吃可可就易如反掌了。于是,聪聪准备马上出发,去找可可。而可怜的可可还不知道大难即将临头,仍在森林里无忧无虑的玩耍。小兔子乖乖听到这件事,马上向灰姑娘报告。灰姑娘决定尽快阻止聪聪,拯救可可,可她不知道还有没有足够的时间。
整个森林可以认为是一个无向图,图中有 \(N\) 个美丽的景点,景点从 \(1\) 至 \(N\) 编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。
当聪聪得到 GPS 时,可可正在景点 \(M\)(\(M \le N\))处。以后的每个时间单位,可可都会选择去相邻的景点(可能有多个)中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有 \(P\) 个景点与景点 \(M\) 相邻,它们分别是景点 \(R\)、景点 \(S\)、……、景点 \(Q\),在时刻 \(T\) 可可处在景点 \(M\),则在 \((T+1)\) 时刻,可可有 \(1/(1 +P)\) 的可能在景点 \(R\),有 \(1/(1 +P)\) 的可能在景点 \(S\),……,有 \(1/(1 +P)\) 的可能在景点 \(Q\),还有\(1/(1 +P)\)的可能停在景点 \(M\)。
我们知道,聪聪是很聪明的,所以,当她在景点 \(C\) 时,她会选一个更靠近可可的景点,如果这样的景点有多个,她会选一个标号最小的景点。由于聪聪太想吃掉可可了,如果走完第一步以后仍然没吃到可可,她还可以在本段时间内再向可可走近一步。
在每个时间单位,假设聪聪先走,可可后走。在某一时刻,若聪聪和可可位于同一个景点,则可怜的可可就被吃掉了。
灰姑娘想知道,平均情况下,聪聪几步就可能吃到可可。而你需要帮助灰姑娘尽快的找到答案。
输入格式
数据的第 1 行为两个整数 \(N\) 和 \(E\),以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。
第 2 行包含两个整数 \(C\) 和 \(M\),以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。
接下来 E 行,每行两个整数,第 \(i+2\) 行的两个整数 \(A_i\) 和 \(B_i\) 表示景点 \(A_i\) 和景点 \(B_i\) 之间有一条路。所有的路都是无向的,即:如果能从 A 走到 B,就可以从 B 走到 A。
输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。
输出格式
输出 1 个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉。
样例 #1
样例输入 #1
4 3
1 4
1 2
2 3
3 4
样例输出 #1
1.500
样例 #2
样例输入 #2
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
样例输出 #2
2.167
提示
【样例说明 1】
开始时,聪聪和可可分别在景点 1 和景点 4。
第一个时刻,聪聪先走,她向更靠近可可(景点 4)的景点走动,走到景点 2, 然后走到景点 3;假定忽略走路所花时间。
可可后走,有两种可能: 第一种是走到景点 3,这样聪聪和可可到达同一个景点,可可被吃掉,步数为 \(1\),概率为\(0.5\)。
第二种是停在景点 4,不被吃掉。概率为 \(0.5\)。
到第二个时刻,聪聪向更靠近可可(景点 4)的景点走动,只需要走一步即和 可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。 所以平均的步数是 \(1\times 1/2 + 2\times 1/2 =1.5\) 步。
【样例说明 2】
森林如下图所示:
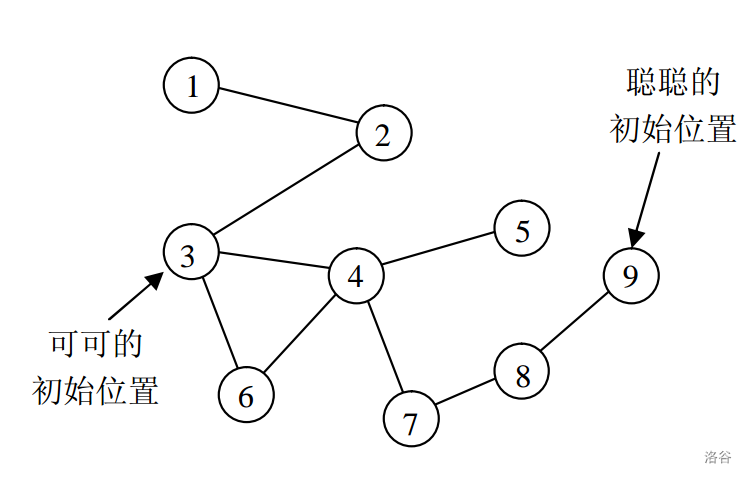
对于 50%的数据,\(1≤N≤50\)。
对于所有的数据,\(1≤N,E≤1000\)。
---------------------------------------------------------------------------------------------------------------------------------------------
题目大意:
1、聪聪的行走方式:(1):所需步数最短。 (2):步数相等先走编号小的。(3):一次最多可走两步。
2、可可的行走方式:可走向邻近的任意一点或留在原地,各种选择概率相同。
3、求聪聪抓到可可的期望步数。
-------------------------------------------------------------------------------------------------------------------------------------------
一、
一开始经过几次手模,发现不管可可怎样走,聪聪都会走最优路线去抓他,所以我打算预处理出聪聪到每个点所需的步数,记为bu[i],然后将每个点的出度(包括自己)记为chu[i].
记录bu数组的时候其实可以不用跑最短路,因为边权是1,直接跑一个BFS就行:
bu[ed]=1;q.push(ed);//ed为聪聪的起点
while(!q.empty()){
x=q.front();q.pop();
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
if(!bu[j]){
// cout<<j<<' '<<bu[x]+1<<"BU\n";
bu[j]=bu[x]+1;q.push(j);
}
}
}
然后依照时间遍历,每次刷表,dp[i][j]代表第j步可可走到i这个地方的概率,dp[i][j]=Σ(dp[k][j-1]/chu[k]),k∈i能走到的点(包括自己)。
于是写出代码:
50'的码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define mk make_pair
#define ps push_back
#define fi first
#define se second
const int N=1e3+10;
int n,m,hd[N],cnt,bu[N],st,ed,chu[N];
double f[N][2];
bool vis[N];
struct jj{
int fr,to,next;
}bi[N<<2];
inline void add(int x,int y){
bi[++cnt]={x,y,hd[x]},hd[x]=cnt;
bi[++cnt]={y,x,hd[y]},hd[y]=cnt;
}
queue<int> q;
int main(){
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
ios::sync_with_stdio(0);cin.tie(0);
cin>>n>>m;
cin>>ed>>st;
bu[ed]=1;
q.push(ed);
int x,y;
while(m--){
cin>>x>>y;
add(x,y);++chu[x],++chu[y];
}
while(!q.empty()){
x=q.front();q.pop();
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
if(!bu[j]){
bu[j]=bu[x]+1;q.push(j);
}
}
}
for(int i=1;i<=n;++i)++chu[i];
int man=0;
for(int i=1;i<=n;++i)bu[i]>>=1,man=max(man,bu[i]);
f[st][0]=1;
for(int i=0;i<=man;++i){
for(int j=1;j<=n;++j){
if(vis[j])f[j][i+1&1]=f[j][i&1];
if(i==bu[j]-1){
vis[j]=1;
f[j][i+1&1]=f[j][i&1];
}
}
for(int j=1;j<=n;++j){
if(vis[j]){
continue;
}
f[j][i&1]/=chu[j];
for(int k=hd[j];k;k=bi[k].next){
int j1=bi[k].to;
f[j1][(i&1)^1]+=f[j][i&1];
}
f[j][(i&1)^1]+=f[j][i&1];
f[j][i&1]=0;
}
}
double ans;
for(int i=1;i<=n;++i){
ans+=f[i][man+1&1]*bu[i];
}
printf("%.3lf",ans);
}
问题出现在哪里?
经过半节数学课的思考,发现bu数组其实不对。
举个例子:

此时1有两种最短路走向2,但因为左侧编号小,所以1只能走左侧,然后2向右走一步。

然后:


一共走了3步。
但如果用bu数组来记得话,就会发现只用走1步。DAMN
所以我们只能预处理出每个点到每个点优先走向哪个点,记为xia数组,xia[i][j]即表示聪聪从i到j要先走哪个点。
for(x=1;x<=n;++x){
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
for(int k=1;k<=n;++k){
if(dis[x][k]-1==dis[j][k])xia[x][k]=min(xia[x][k],j);//dis[i][j]代表i与j的距离。
}
}
}
最后我们只需要记搜一下即可,记得处理边界。
$\Huge{niumo}$
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define mk make_pair
#define ps push_back
#define fi first
#define se second
const int N=1e3+10;
int n,m,hd[N],cnt,bu[N],st,ed,chu[N],dis[N][N],xia[N][N];
double f[N][N];
bool vis[N],v[N][N];
struct jj{
int fr,to,next;
}bi[N<<2];
inline void add(int x,int y){
bi[++cnt]={x,y,hd[x]},hd[x]=cnt;
bi[++cnt]={y,x,hd[y]},hd[y]=cnt;
}
inline void dfs(int x){
queue<int> q;
dis[x][x]=1;q.push(x);
while(!q.empty()){
int k=q.front();q.pop();
for(int i=hd[k];i;i=bi[i].next){
int j=bi[i].to;
if(!dis[x][j])dis[x][j]=dis[x][k]+1,q.push(j);
}
}
}
inline double ask(int x,int y){
if(v[x][y])return f[x][y];
if(x==y)return 0;
int to1=xia[x][y],to2=xia[to1][y];
f[x][y]=1;v[x][y]=1;
if(to1==y||to2==y)return 1;
for(int i=hd[y];i;i=bi[i].next){
int j=bi[i].to;
f[x][y]+=ask(to2,j)/chu[y];
}
f[x][y]+=ask(to2,y)/chu[y];
return f[x][y];
}
int main(){
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&ed,&st);
int x,y;
while(m--){
scanf("%d%d",&x,&y);
add(x,y);
++chu[y],++chu[x];
}
for(int i=1;i<=n;++i){
dfs(i);++chu[i];
}
for(int i=1;i<=n;++i)
for(int j=i+1;j<=n;++j)xia[i][j]=xia[j][i]=0x3f3f3f3f;
for(x=1;x<=n;++x){
for(int i=hd[x];i;i=bi[i].next){
int j=bi[i].to;
for(int k=1;k<=n;++k){
if(dis[x][k]-1==dis[j][k])xia[x][k]=min(xia[x][k],j);
}
}
}
printf("%.3lf",ask(ed,st));
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号