论文学习笔记:A Network-Based High Level Data Classification
论文学习笔记:A Network-Based High Level Data Classification
Technique , 该论文介绍了一种基于网络的高级数据分类技术
1. 训练过程简述
整体思想是, 训练过程先形成一个网络, 而预测过程则是, 新数据进入网络, 最接近该网络原始的内部模式和网络结构的插入位置, 作为该数据的标签.
- 把数据集切分成:\(X_{trainning}和Y_{trainning}\)
- \(把X_{training}切分成:X_{net}和X_{items}, Y_{trainning}做同样的切分\)
- 那么一个网络就由多个
组件来形成一个网络, 每个子集代表一类标签的数据 组件指的是网络中同一个标签的节点集.- 为每个网络当中
组件提取一些网络测度,作为其影响网络的值, 注意这里的网络测度可以有多个方法 - \(将每一个X_{item}逐一添加至网络当中, 每次有新节点插入,\) 那么网络当中被影响的组件的
网络测度会被重新计算 - 需要注意的是, 在训练阶段, 每次有新的节点插入, 只会影响到一个组件的
网络测度, 因为这个节点是有标签的。 - 训练过程中,将每次插入新节点对组件造成的网络测度的变化,作为一个影响值, 存入一个二维数组里边, 最后作为影响列表
- 在预测阶段, 把新节点插入生成的影响值, 与原有的网络度量状态比较, 相差最小,使网络趋于稳定的那个插入即为新节点的标签.
2. 算法的详细
构建网络
- 两个超参数\(k和p\) : 其中\(k用于kNN算法寻找最近的k个点, p用于将划分X_{trainning}划分成X_{net}和X_{item}的比例\)
- \(X_{net}用来初始化一个网络, X_{item}用来训练, 逐个添加至网络\)
- 先用\(X_{net}\)构建初始网络, 使用两个经典的网络构建方法组合如下:
\[N(x_i)=
\begin{cases}
\epsilon-radius(x_i, y_i)& ,{if|\epsilon-radius(x_i, y_i)|>k}\\
kNN(x_i, y_i)& ,\text{otherwise}
\end{cases}\]
- \(N(x_i)表示x_i的邻域节点\)
- 其中第一种情况表示, 以\(x_i为原点, 以\epsilon为半径, 如果x_i的邻域的节点数大于k个, 那么按照第一种算法找\)
- 否则按照KNN算法找
- 其中
\[\epsilon=\sum_{j=1}^L\frac{median(kNN_{dist}(x_i,y_{x_i}))}{L}
\]
- \(kNN_{dist}(x_i,y_y)返回的是k个距离x_i最近的距离\)
- L是标签数量
训练
- 网络构建完成后. \(将X_{item}逐个添加至网络当中, 每个x_i造成的影响(1维数组,维度=选取的网络测度方法数)是\)
\[I_i^{(j)}(x)(u)=\Delta G_i^{(j)}(u)\rho^{(j)}
\]
- \(u: 表示第u个网络测度方法\)
- \(j:表示第j个类别\)
- \(I_i^{(j)}(x)(u): 表示节点i在标签(组件)j中的网络测度u的影响值\)
- \(\Delta G_i^{(j)}(u)\in[0,1]: 表示节点i插入到组件j中, 其网络测度的变化值\)
- \(\rho^{(j)}\in[0,1]: 表示该组件中节点的数量占总数量的比值\)
- 要训练的参数. 我们有了网络测度. 对这几个网络测度进行加权, 并训练优化这些权重, 该权重数组是二维的,第一维代表网络中组件(类别的)索引,第二维代表了测量方法的索引, 每种组件的测量方法的权重求和为1:
\[\sum_{u=1}^K\alpha(u)=1
\]
- \(u: 表示网络测度\)
预测部分
给一个\(x_i\in X_{test}, 它没有标签, 那么它在网络测度下的影响值也就等于\)
\[f_i^{(j)}(x)(u)=\alpha ^{(j)}(u)I_i^{(j)}(x)(u)
\]
- \(j:表示类别\)
- \(u:表示网络测度方法\)
节点对组件j产生的影响值与组件J之前的影响值的最小距离为:
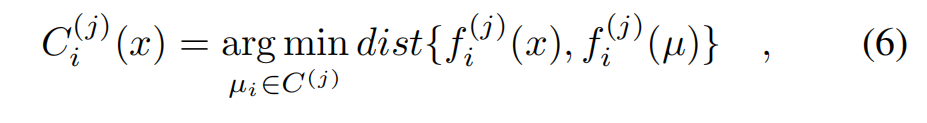
节点属于组件j的概率:
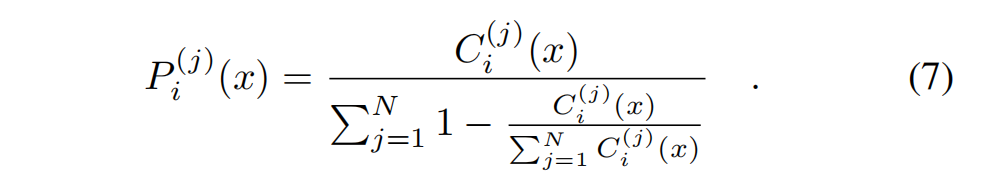
论文中给的网络度量法:
- Average degree (hki):
- Assortativity (r)
- Average local clustering coefficient (hccii)
- Transitivity (C)
- Average shortest path length (l):
- Second moment of degree distribution (hk2i):
