第四章--度相关性和社团结构(复杂网络学习笔记)
前言
为进一步刻画网络的拓扑结构, 引入高阶拓扑特性。本章介绍了二阶度分布特性(也叫度相关性)的几种不同的方法,包括联合概率分布,条件概率和余平均度等...
度相关性和同配性
度相关性
- 平均度: \(<k>=\frac{2M}{N}\) ,
0介度分布特性 - 度分布: \(P(k)=n(k)/N\),
1介度分布特性, 其中\(n(k)\)表示度为k的节点的个数, 如果随机选择一个节点\(i\),那么它度为\(k\)的概率就是\(P(k)\), - 显然,
1介度分布特性已经包含0介度分布特性
\[<k> = \sum_{k=0}^{\infty}kP(k)
\]
联合概率分布(二阶度分布)
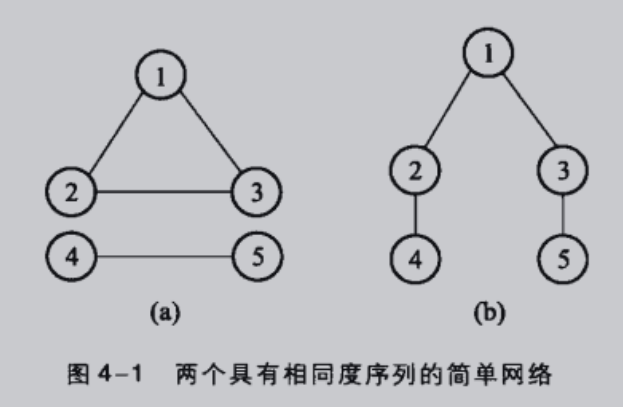
显然,如上图,两个具有相同的度分布的网络,其网络结构方面也有很大区别, 因此引入 联合概率分布.
定义
有两种定义
- 联合概率\(P(i, j)\)定义为网络中随机选取的一条边, 该边连接的两个端点的度分别为\(i和j\)的概率
- 联合概率\(P(i, j)\)定义为网络中端点的度分别为\(i和j\)之间的边数占
总边数的比例
\[P(j,k)=\frac{m(j,k)\mu(j,k)}{2M}
\]
- \(其中m(j, k)是度分别为j和k的节点的连边数\)
- \(如果j=k,那么\mu(j,k)=2, 否则\mu(j,k)=1\)
联合概率分布具有以下性质
- 对称性
\[P(i,j) = P(j, i)
\]
- 归一化
\[\sum_{i,j}^{\infty}P(i,j)=1
\]
- 余度分布(Excess degree distribution)
\[P_n(k)=\sum_{j=k_{min}}^{k_{max}}P(j,k)
\]
- \(其中k_{min},k_{max}分别表示网络中度的最小和最大值,\)
- \(P_n(k)表示:网络中随机挑选一个节点, 该节点与度为k的节点相连的概率\)

余平均度
这里介绍另一种判断度相关性的方法:
条件概率

如上, 如果条件概率\(P_c(j|k)与k相关\),那么就说明节点之间具有度相关性,并且网络拓扑可能具有层次结构 否则就不具有度相关性.
余平均度

同配系数
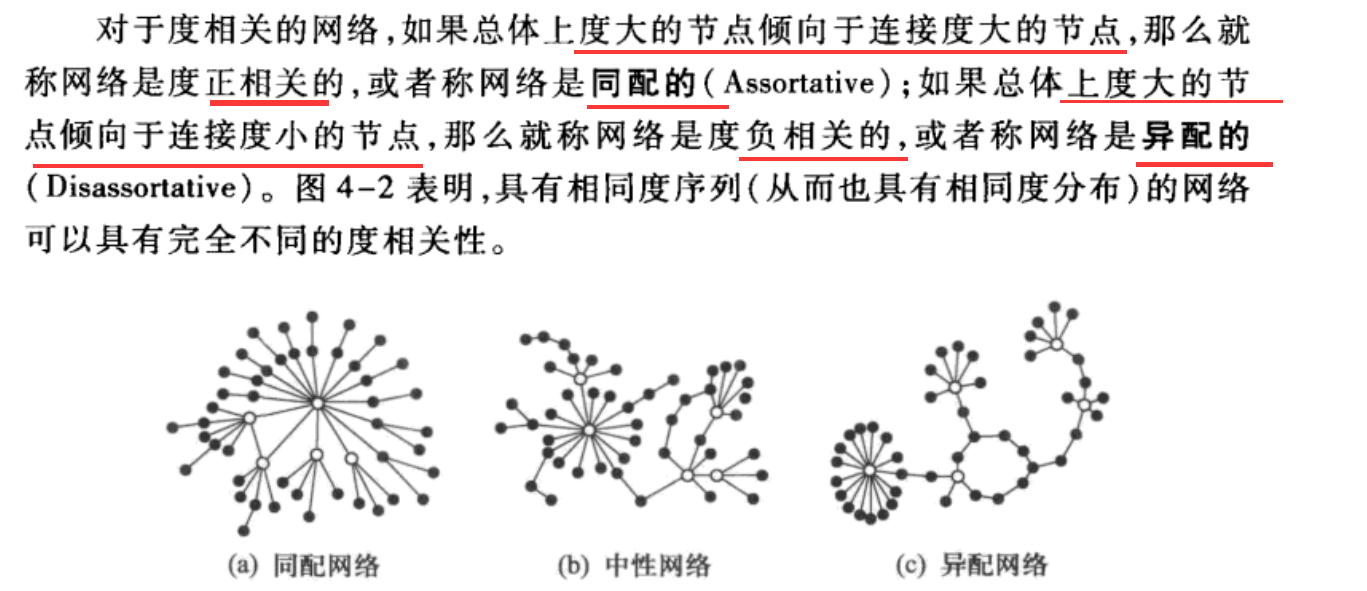
进一步介绍如何用一个指标值来刻画网络是同配还是异配.


社团结构与模块度
分类聚类是寻找社会网络中社团结构的一类传统算法, 该类算法分为两类: 凝聚算法(Agglogmerative method)和分裂算法(divisive method)
模块度(modularity)
模块度是今年常用的一种衡量社团划分质量的标准, 其基本的想法是把划分社团后的网络与相应的零模型(Null method)进行比较,以度量社团划分的质量.
- 零模型: 一个网络的零模型指的是, 与该网络具有相同的性质(如相同的边数或相同的度分布)而在其他方面完全随机的随机图模型, 第六章会介绍.
模块度的概念:
\[Q_{real}=\frac{1}{2}\sum_{ij}a_{ij}\delta(C_i,C_j)
\]
- \(其中A=(a_{ij})\),是实际网络的邻接矩阵
- \(C_i和C_j分别表示节点i和节点j在网络中所属的社团\)
- \(如果i,j属于同一个社团,那么\delta(C_i,C_j)=1, 否则\delta(C_i,C_j)=0\)


