第二章--网络与图(复杂网络学习笔记)

网络与图

图的定义

• 图的数学表示:\(G=(V, E)\)
• 节点数: \(N=|V|\), 边数\(M=|E|\)

图的类型

• 按照边的方向分为: 有向图和无向图
• 按照边的权值分为: 加权图和无权图

简单图

本书重点介绍无权无向图.

• 重边: 两个节点之间只有一条边
• 自环: 没有以同一个节点为起止点的边
• 简单图:没有重边且没有自环的图
• 如下图所示: 非简单图
  

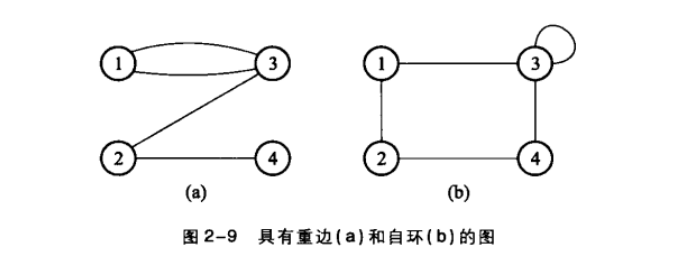
简单图的两种极端情形:

1. 空图(Null Graph): 它有两种定义,一是指没有任何节点和连边的图;二是指没有任何连边的图.
2. 完全图(Complete Graph): 任意两个节点之间都有一条连边, 即边数为\(\frac{1}{2}N(N-1)\)

稀疏网络: 网络中的边数与\(N\)同阶

图的计算机表示

两种最常见的网络表示方法:邻接矩阵(Adjacency Matrix)和邻接表(Adjancency list)

1. 邻接矩阵

令有一个N个节点的图G, 那么其邻接矩阵大小为\(N*N\),其中元素为

\[a_{ij}= \begin{cases} w_{ij}& \text{节点i指向节点j的边的权值}\\ 0& \text{节点i与节点j之间没有连边} \end{cases}\]

如一个邻接矩阵:

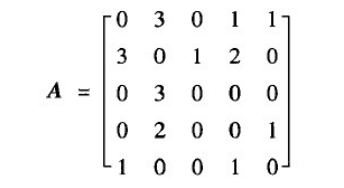
2. 邻接表与三元组

邻接表

在图算法中,表示稀疏的无权图最常用的方法就是邻接表.

以网络中的每个节点为单位, 生成一个对应的单链表。
例如有5个节点(1,2,3,4,5)的图,其邻接表表示如下:

三元组

三元组表示方法如下:

其第一行的(1,2,3)表示: 从节点1到节点2有一条权值为3的边.

3. 共引网络和文献耦合

共引网络(无向)

因为无向网络的发展比较成熟, 所以一般把有向网路问题转化为无向网络来进行研究.

共引网络: 假如有两篇文献.被一篇其他的文献同时引用,那这两篇文献之间就会生成一条边,生成网络.

文献耦合网络

文献耦合网络: 假如有两篇文献, 他们共同引用了同一篇文献, 那这两篇文献之间就会产生一条权值为1的边.

4. 路径和连通性

令一个无向网络:\(G=(V, E)\)

1. 路径(path): 指一个顶点到另一个顶点的路径,表示为一个顶点序列\(P=V_1,....V_5\),
2. 回路(circuit): 起点和终点重合的路径称为回路.
3. 简单路径(simple path): 路径中的顶点各不相同.
4. 圈(circle) : 圈是一个回路,一个圈只有起点和终点相同,其他都互不相同.

连通性(Connected)

• 连通图: 任意两个节点之间都存在一条路径, 反之则为不连通的.

路径和连通性的邻接矩阵表示

网络中的两个节点之间往往可能存在不止一条路径,并且每条路径的长度可能也不一致.

• 设有邻接矩阵\(A=(a_{ij})_{N*N}\)
• 怎样求节点i和节点j是否有长度为2的路径?

看下图(连通性推导过程)

割集和Menger定理

在网络科学研究中,网络的鲁棒性是一个重要课题.考虑以下:

如果在一个图G中去除了一些边和节点,那么之前给定的节点\(S和T\)之间是否仍然存在路径(是否仍然处于同一个连通片)?

鲁棒性的分析会在以后的章节给出,这里给出Menger定理.

Menger定理

给出下面两种形式的定义:

• 点形式: 设顶点s和顶点t为图中不相邻的两个节点,则使它们分别属于不同的连通片所需要去除的顶点的最少数量等于连接顶点s和顶点t的独立简单路径的最大数目.
• 边形式: 所需要去除的边的最少数目等于连通顶点s和顶点t的不同相交的简单路径的最大数目.

下面定理中的术语:

1. 两个节点之间独立简单路径: 所有路径只有起始节点是一样的,其他节点均不一样的, 独立简单路径之间互不相交
2. 点割集: 使得一对节点分别属于不同的连通片所需去除的节点的集合叫做点割集
3. 边割集: ..........................................边............边割集

有向图的连通性

强连通: 任意一对顶点都有你来我往的两条边.
弱连通: 如果把有向图中的边直接转换为无向的, 那么如果该无向图是连通的,成为弱连通

生成树与最小生成树

树

一个包含N个顶点的连通图G至少包含N-1条边, 如果这个连通图刚好只有N-1条,这个图就是个最简单的连通图,我们称之为树
一般地, 包含下面任意条件之一都可称之为树:

1. 图G是连通的,只有N-1条边
2. 图G是连通的,不包含圈
3. 图G是不包含圈,且只有N-1条边
4. 图G任意一对顶点只有一条路径
5. 去掉图G任意一条边,都会使得图G不连通

如下图: 简单连通图,画成树的样子.

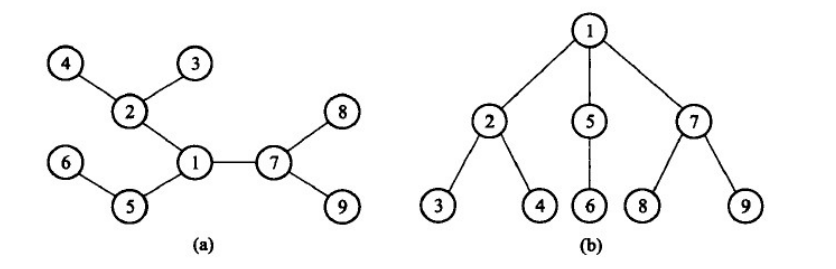
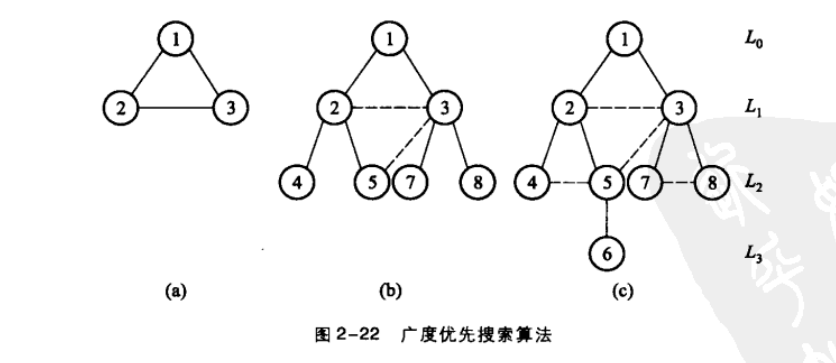
广度优先搜索算法

具体算法涉及数据结构算法,可自行查阅,大致思路如下图:

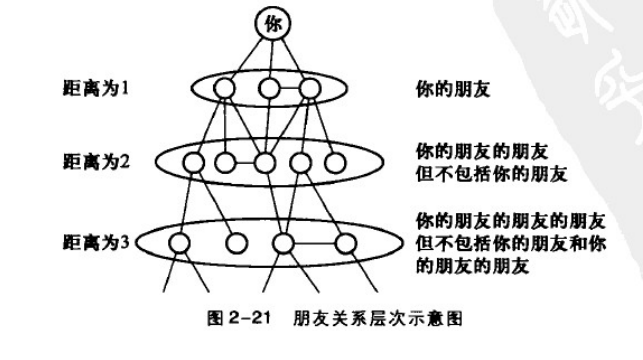
最小生成树

概念: 如果一个连通图不是树, 那么就可以看做是在一个树的基础上添加一些边而形成的, 那么就引入了生成树的概念.

• 连通图的生成树是该连通图的一个子图
• \(N\)个顶点的连通图可能包含多个生成树, 每个生成树的边数一定是\(N-1\)
• 一个完全图的生成树的数量有Caylay公式: \(\tau=N^{N-2}\)

生成树的概念如果推广到加权无向图中, 那么

• 最小生成树: 该生成树的边的权值最小的那个,
• 最小生成树的数量不一定是唯一的, 当图中边的权值互不相同,那么必然只有唯一一种最小生成树

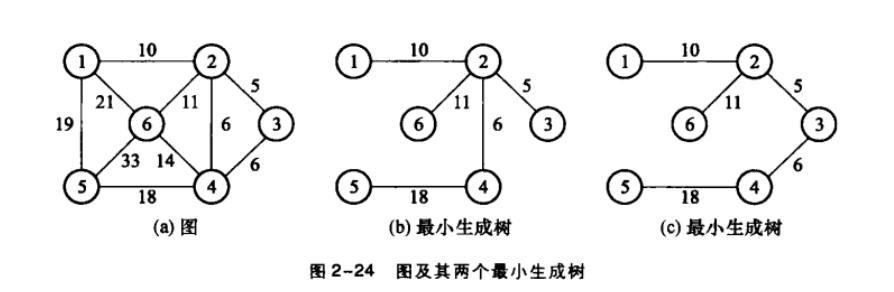
最小生成树的两种方法（Kruskal算法和Prim算法）

参考博客: https://blog.csdn.net/a2392008643/article/details/81781766

二分图和匹配问题

二分图的定义

二分图的匹配

比如以人员和资源分配问题 或者 学生选择导师问题,可以构成二分图的匹配问题.

稳定匹配

二分图中稳定的完全匹配算法,内容包括稳定匹配的求解,稳定匹配的公平性,和稳定匹配的存在条件,可自行了解查阅资料