神经网咯基础-deeplearning.ai【笔记】
目录
Basement of Neural Network
1. Logistic Regreesion
\(逻辑回归一般输出为[0, 1], 用来解决二分类问题。\)
1.1 Some Notation
Ng给出的一些符号的解释
- \((x,y): 表示样本的输入x和输出y\),
- \(m: 表示样本数量\)
- \(n: 输入x的特征数\)
- \(x\in R^n:表示x是一个n维实数向量。其中R^n表示n维实数向量，是线代的一般符号表示。\)
- \(y\in\lbrace0,1\rbrace : 目标值属于0、1分类\)
- \(\lbrace (x^{(1)},y^{(1)}) , (x^{(2)},y^{(2)}), (x^{(m)},y^{(m)})......\rbrace：表示一组训练数据\)
- \(w：表示参数向量，w\in R^n\)
- \(x_i:表示该样本的第i个特征。\)
- \(w_i:表示参数向量的第i个特征。\)
- \(b : bias, 偏差\)
\(那么给定一些数据集X，和这些数据集的标签Y，即可学习其映射关系，而后利用该映射关系即可计算其他新数据的标签\)
- 先从简单线性组合开始, 假设数据只有3个特征：
\[H(X)= w^TX + b= Y
\]
\[H(x) = w^T[x^1\ x^2\ x^3] + [b_1\ b_2\ b_3] = [y^1\ y^2\ y^3]
\]
\[H(X)= \left[
\begin{matrix}
w_1 & w_2 & w_3 \\
\end{matrix}
\right]
\left[
\begin{matrix}
x_1^1 & x_1^2 & x_1^3 \\
x_2^1 & x_2^2 & x_2^3 \\
x_2^1 & x_3^2 & x_3^3 \\
\end{matrix}
\right]+ [b_1\ b_2\ b_3] =[y^1\ y^2\ y^3]\]
1.2 Hypothesis
- \(假设一个模型，给定输入x，逻辑回归可以输出其是猫(y=1)的概率：\)
\[\hat{y} = P(y=1\mid x)
\]
- \(这里引入sigmoid\ function，该函数可以将z映射到[0, 1]区间\)
\[\sigma(z) = \frac{1}{1+e^{-z}}
\]
-
\(where\ z=w^Tx+b，当z趋向于无穷大，\sigma(z)趋向1；反之\sigma(z)趋向于0\)
-
最终我们的Hypothesis function:
\[H(x) = \hat{y}(x) = \frac{1}{1+e^{-(wx+b)}}
\]
为了训练得出参数\(w和b\),下面引出cost function
1.3 cost function
\(Given\ \lbrace (x^{(1)},y^{(1)}) , (x^{(2)},y^{(2)}), (x^{(m)},y^{(m)})......\rbrace,want\ \hat{y}^{i}\approx y^i\),
- 引出Loss(Error) funtion
\[L(\hat{y},y) = \frac{1}{2}(\hat{y}-y)^2
\]
- 这样便定义了损失函数，最优化该损失函数求得\(w和b\)
- 但是这个函数是非凸函数, 难以求得最优解
- 引出新的损失函数, 它是个凸函数
\[L(\hat{y},y) = -(ylog\hat y + (1-y)log(1-\hat y))
\]
- \(加个-号是为了让L\geq 0\)
- 当\(y=1时,L(\hat{y},y) = -ylog\hat y, 如果希望损失变小,则\hat y 就要越大,越接近1\)
- 当\(y=0时,L(\hat{y},y) = -log(1-\hat y), 如果希望损失变小,则\hat y 就要越小,越接近0\)
Loss function是在单个训练样本中定义的,衡量了Hypothesis在单个样本上的性能
最终引出Cost function, 它衡量了全体样本的性能
\[J(w,b) = \frac{1}{m}L(\hat{y}^i,y^i)
\]
\[J(w,b) = -\frac{1}{m}\sum_{i=1}^m[y^ilog\hat{y}^i + (1-y^i)log(1-\hat{y}^i)]
\]
- 怎样训练,最终求得cost function的最优解? 引出梯度下降.
1.4 logistic regression Gradient Descent
- 两个梯度下降的图解
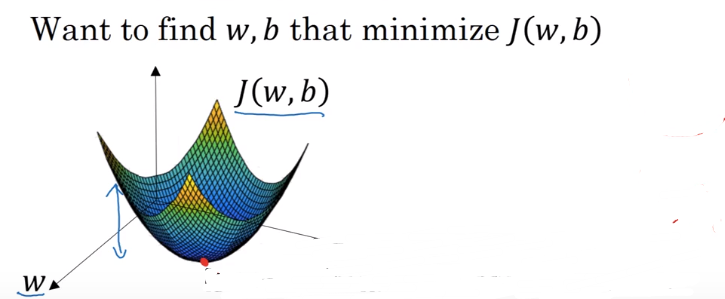
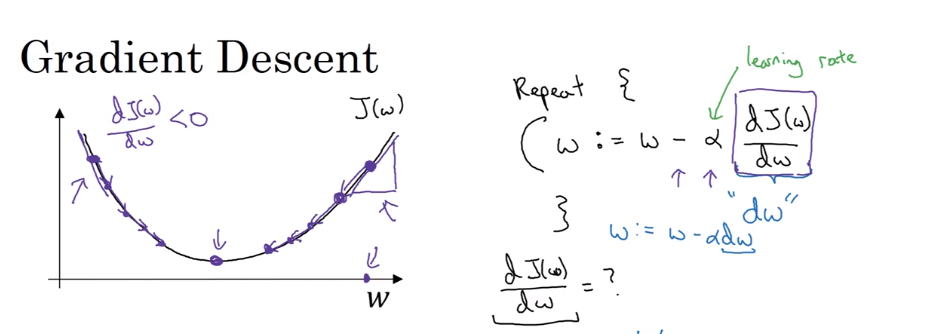
单个样本的梯度下降
- 回顾公式:
\[z = w^Tx +b
\]
\[a= \sigma (z)=\frac{1}{1+e^{(-z)}}
\]
\[L(a,y) = -[yloga + (1-y)log(1-a)]
\]
- 梯度下降:
\[w = w - dw = w - \frac{\partial J(w,b)}{\partial w}
\]
\[b = b - db = b - \frac{\partial J(w,b)}{\partial b}
\]
- 链式求导:
\[dw = da\frac{da}{dz}\frac{dz}{dw}
\]
\[db = da\frac{da}{dz}\frac{dz}{db}
\]
- 计算其中:
\[da = -(\frac{y}{a}=\frac{1-y}{1-a})
\]
\[\frac{\partial da}{\partial dz} = \frac{e^z}{(1+e^{-z})^2} = \frac{1}{1+e^{-z}}\frac{e^{-z}}{1+e^{-z}} = a(1-a)
\]
\[\frac{\partial dz}{\partial dw} = x
\]
\[\frac{\partial dz}{\partial db} = 1
\]
- 最终得出:
\[dw = \frac{1-y}{1-a}a(1-a)x = (a-y)x
\]
\[db = \frac{1-y}{1-a}a(1-a) = (a-y)
\]
给定学习率\(\alpha\),则可以迭代学习参数
\[w = w-\alpha dw
\]
\[b = b-\alpha db
\]
多个样本的梯度下降
\[dw = \frac{1}{m}\sum_{i=1}^m(a^i-y^i)x^i
\]
\[db = \frac{1}{m}\sum_{i=1}^m(a^i-y^i)
\]
\[w = w-\alpha dw
\]
\[b = b-\alpha db
\]
1.5 Vectorization
样本量大,使用for循环来进行迭代训练模型,效率很低.这里引入向量化技巧。利用矩阵运算代替循环迭代以提速。
这里首先要理解两个概念:
np.dot中有:
- 如果处理的是一维数组，则得到的是两数组的点积,即元素对应相乘,而后相加
- 如果处理的是高维数组，则计算的是矩阵相乘的结果。
维度:
- \(X : (n, m)\)
- \(Y : (1, m)\)
- \(W: (n,1): 参数\)
- \(b:(1, m): 偏置参数\)
- \(Z:(1, m): 线性组合\)
- \(A:(1, m): 激活函数\)
- \(J:(1, 1): 代价函数\)
向量化数学公式：
\[Z = W^Tx+b =[w_1,w_2][x^1,x^2]+b= [w_1,w_2]
\]
\[\left[
\begin{matrix}
x_1^1 & x_1^2 \\
x_2^1 & x_2^2
\end{matrix}
\right]+[b_1,b_2] = [z^1,z^2]
\]
\[A = sigmoid(Z) = [\sigma(z^1)\ \sigma(z^1)]
\]
\[J = -\frac{1}{m} [YlogA+(1-Y)log(1-A)]
\]
\[J = -\frac{1}{m} \lbrace [y^1\ y^2]*log[a^1,a^2] + (1-[y^1, y^2])*log[1-a^1,1-a^2] \rbrace
\]
\[dW = (A-Y)X = \frac{1}{m}[dw^1,dw^2]
\]
\[db = (A-Y) = \frac{1}{m}[db^1,db^2]
\]
\[W = W -dW
\]
\[b = b-db
\]
