1- 基本概念(复杂网络学习笔记)
复杂网络
1. 基本概念
- 网络的图表示 ：\(G=(V，E)\)，
- 节点数 ：\(N=|V|\)
- 边数 : \(M=|E|\)
- 有向网络,无向网络 : 任一点对\((i, j)和(j, i)\)对应同一条边,则为无向网络,反之成为有向.
- 有权网络,无权网络 : 边有权值, 成为有权. 反之,无权
- 两个节点的距离:
定义为两节点之间最短路径长度: \(d_{ij}\) - 网络的直径:
网络中中任意两个节点距离的最大值: \(D=max(d_{ij})\) - 平均路径长度 :
定义为任意两个节点之间距离的平均值: \(L=\frac{1}{\frac{1}{2}N(N+1)}\sum_{i\geq j}d_{ij}\)
为了方便数学处理,在公式中包含节点到节点自身的距离,所以是\(N(N+1)\), 乘\(\frac{1}{2}\)是因为无向网络.
如下图示:
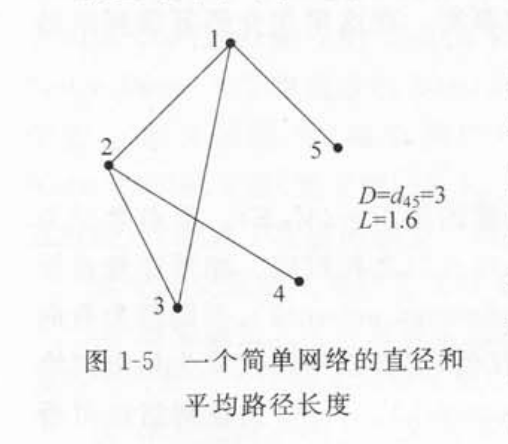
2. 聚类系数
- 网络中1个节点 \(i\) , 有 \(k_i\) 条边与之相连,
- 也就是 \(i\) 有 \(k_i\) 个邻居节点
- 显然, 这\(k_i\)个节点之间最多可能有\(k_i(k_i-1)/2\)条边.
- 设这\(k_i\)个节点之间真实边数为\(E\)
- 则节点 \(i\) 的聚类系数:
\[C_i=\frac{E}{k_i(k_i-1)/2}=\frac{2E}{k_i(k_i-1)}
\]
从几何的特点看: 上式等价为:
\[C_i=\frac{与点i相连的三角形数量}{与点i相连的三元组的数量}
\]
- 其中:与点
i相连的三元组是指包括点i的三个节点,并且至少存在从节点i到其他两个节点的两条边.如下图所示:
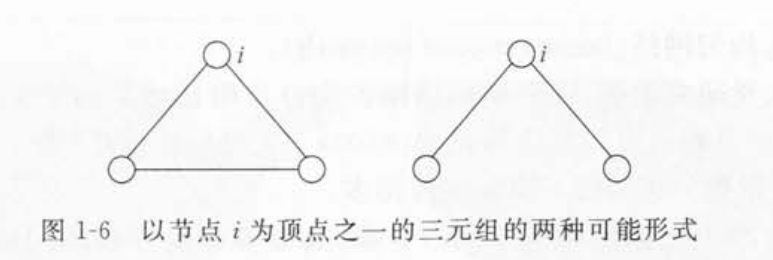
- 整个网络的聚类系数 : \(C=\frac{1}{N}\sum_NC_i\) , 即为所有节点聚类系数和的平均值.
3. 度与度分布
- 节点 \(i\) 的度: \(k_i\) ,定义为与节点 \(i\) 相连的节点的数量.
- 出度 : \(i\) 指向 邻居节点的边的数目
- 入度 : 邻居节点指向\(i\)的边的数目
- 网络节点的平均度 : \(k = \frac{1}{N}\sum_N k_i\)
度分布
- 网络中节点度的分布情况可以用\(P(k)\)表示, 其中\(P(k)\) 定义为网络中度为\(k\)的节点在整个网络中所占的比率.
- 规则的格子有着简单的度序列:因为所有的节点具有相同的度,所有其度分布为
Delta分布,它是单个尖峰. - 完全随机网络的度分布近似
Poisson分布.这类网络也称为均匀网络. - 幂律分布也称为无标度分布,这类网络称为无标度网络.
