4-几何概型/频率/公理化(概率论与数理统计学习笔记)
几何概率模型
概念 :如果每个事件发生的概率只与构成该事件区域(长度\面积\体积)成正比,则称这种概率模型为几何概型。
概率和频率
频率:\(n\)次试验,事件\(A\)发生了\(m\)次, 频率表示为: \(\omega_n(A)=\frac{n}{m}\)
公理化
- 非负性: \(0\leq P(A) \leq 1\)
- 规范性: \(P(\Omega) = 1\)
- 可加性: \(A_1,A_2.....\)互不相容,\(P(A_1+A_2+....+A_n)=P(A_1)+....+P(A_n)\)
性质
- \(P(\emptyset)=0\)
- \(A_1,.....A_n\)互不相容,则\(P(A_1+A_2+....+A_n)=P(A_1)+....+P(A_n)\)
- \(P(\overline{A}) = 1 - P(A)\)
- \(P(A-B) = P(A) -P(AB)\)
- \(A\subset B,P(A-B) = P(A)-P(B)\) ,
- 加法公式: \(P(A+B)=P(A)+P(B)-P(AB)\)
例题

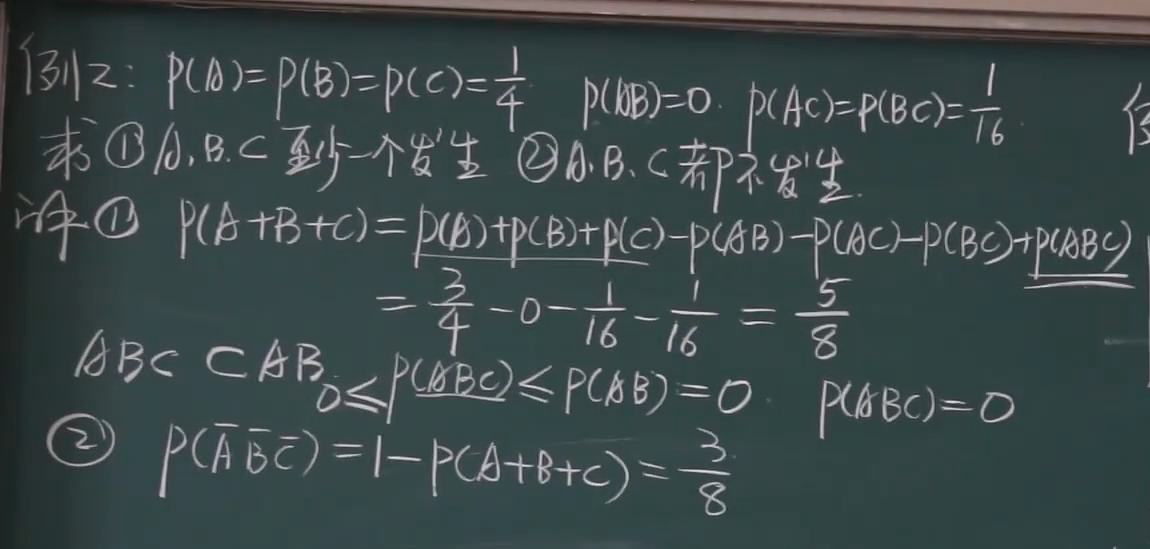



 浙公网安备 33010602011771号
浙公网安备 33010602011771号