DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
0.PTA得分截图

1.本周学习总结
树存储结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合
1.1 二叉树结构
n结点的有限集合,由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成
1.1.1 二叉树结构
- 特点:
1.每个结点最多有2个孩子
2.子树有左右之分,其次序不能颠倒
3.二叉树可以是空集合,根可以有空的左子树或有空的右子树
- 3个结点二叉树的五种基本形态
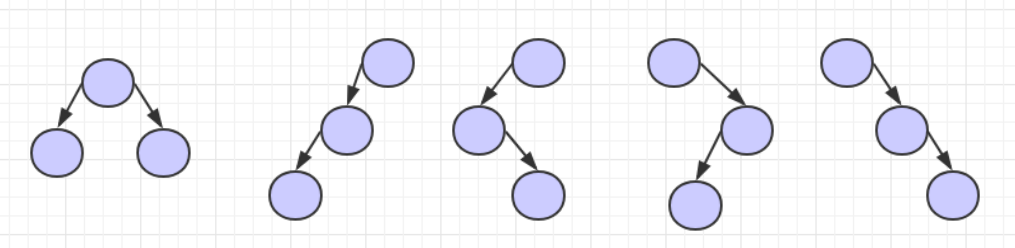
- 性质:
1.非空二叉树上叶节点数等于双分支节点数加1
证明:
①设二叉树上叶节点数为n0,单分支(度为1)节点数为n1,双分支(度为2)节点数为n2,则总节点数n=n0+n1+n2。
②在一棵二叉树中,所有节点的分支数(即度数)应等于单分支节点数加上双分支节点数的2倍.
因为n=1*n1+2*n2,即总的分支数=n1+2n2。
③由于二叉树中除根节点以外,每个节点都有唯一的一个分支指向它,因此二叉树中有:总的分支数=总节点数n-1。
因为②=③,n1+2n2=n-1,整理以后:n=n1+2n2+1=①;
得出n1+2n2+1=n0+n1+n2,即:n0=n2+1
求解二叉树的节点个数问题:通常利用二叉树的性质1,即n0=n2+1来求解这类问题,也常利用以下关系求解:
总节点数n=叶节点数n0+单分支节点数n1+双分支节点数n2
而度之和=n-1或度之和=n1+2n2
所以有:n=n1+2n2
求解完全二叉树的节点个数问题:完全二叉树属于二叉树,也满足二叉树的性质1,即n0=n2+1。
除此之外,完全二叉树中一旦n确定,其树形就确定了,可以计算出高度h以及n0、n1和n2。其中n1=0或1,当n为偶数时,
n1=1,当n为奇数时,n1=0。其关系有:h=log2n+1或h=log2(n+1)
求解满二叉树的节点个数问题:满二叉树是最严格的二叉树,一旦n确定,其树形就确定了。
可以计算出高度h以及n0、n1和n2。其关系有:h=log2(n+1),n1=0,n=2h-1,n0=2h-1,n2=2h-1-1
2..在二叉树的 i 层上至多有 2^(i-1) 个结点(i>=1)(满二叉树时最多)
3.深度为 k 的二叉树至多有 2^k-1 个结点(i>=1)
4.对任何一棵二叉树 T,如果其终端结点树为 n0,度为 2 的结点为 n2,则 n0 = n2 + n1
5.具有 n 个结点的完全二叉树的深度为 [log2n] + 1 向下取整
6.如果有一棵有 n 个结点的完全二叉树(其深度为 [log2n] + 1,向下取整)的结点按层次序编号(从第 1 层到第 [log2n] + 1,向下取整层,每层从左到右),则对任一结点 i(1 <= i <= n)有
①如果 i = 1,则结点 i 是二叉树的根,无双亲;如果 i > 1,则其双亲是结点 [i / 2],向下取整
②如果 2i > n 则结点 i 无左孩子,否则其左孩子是结点 2i
③如果 2i + 1 > n 则结点无右孩子,否则其右孩子是结点 2i + 1
1.1.2 二叉树的2种存储结构
1.1.2.1树的顺序存储结构
二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。因此,必须把二叉树的所有结点安排成为一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系,用编号的方法从树根起,自上层至下层,每层自左至右地给所有结点编号
- 完全二叉树
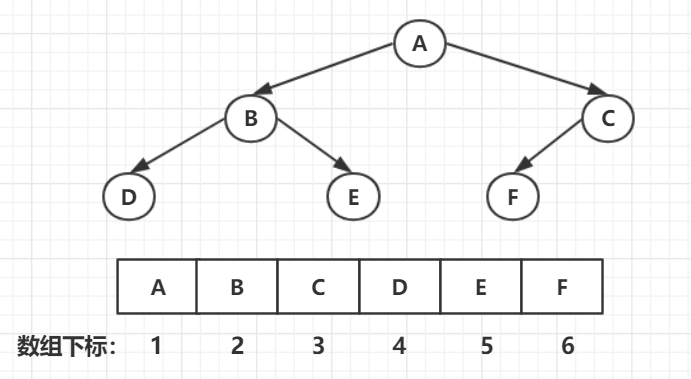
(a) 一棵完全二叉树 (b) 顺序存储结构
- 非完全二叉树
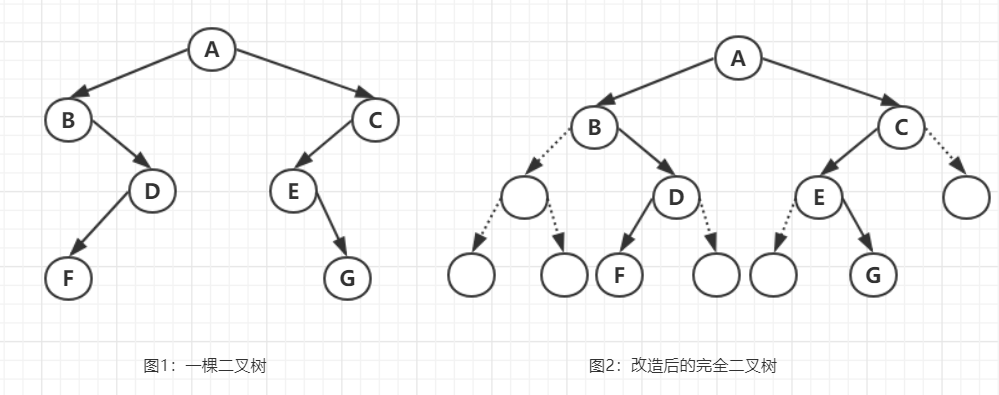

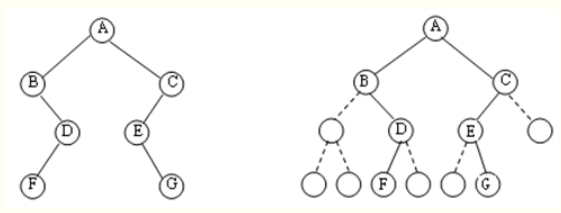
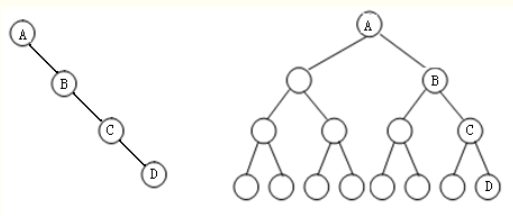
(a) 一棵右单支二叉树 (b) 改造后的右单支树对应的完全二叉树

(c) 单支树改造后完全二叉树的顺序存储状态
定义
typedef ElemType sqBTree[MaxSize];
1.1.2.2树的链式存储结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。

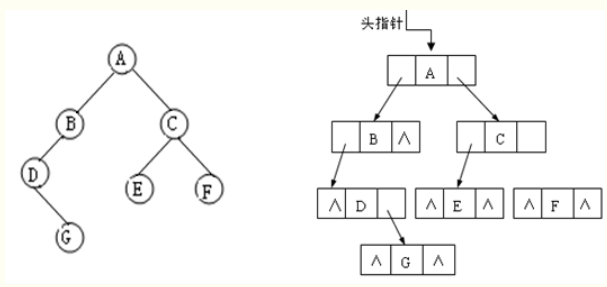
(a) 一棵二叉树 (b) 二叉链表存储结构
定义
typedef struct BTNode
{
ElementType data;//结点数据
BTree lchild;//指向左孩子
BTree rchild;//指向右孩子
}BTNode,*BTree;
递归性:递归指向的都是二叉树
1.1.3 二叉树的构造
- 顺序存储结构转二叉链(直至读取到“#”结束)
void CreateBTree(BTree &bt,string str, int i)
{
int len;
len = str.size();
bt = new TNode;
if (i > len || i < 1)
{
bt=NULL;return;
}
if (str[i] == '#')
{
bt=NULL;
return;
}
bt->data = str[i];
CreateBTree2(bt->lchild,str, 2 * i);
CreateBTree2(bt->rchild,str, 2 * i + 1);
}
- 先序遍历建二叉树
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->data = str[i];
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
return bt;
}
- 已知先序和中序遍历序列构造二叉树
根据先序遍历的特点, 知先序序列的首个元素为二叉树的根,然后在中序序列中查找此根, 根据中序遍历特点, 知在查找到的根前边的序列为根的左子树的中序遍历序列。
我们可以求得根节点左子树的先序和中序序列,以及右子树的先序和中序序列。
此问题变成了根据左子树的先序和序列构建左子树的二叉树,根据右子树的先序和中序序列构建右子树的二叉树问题得以分解成子问题。
BTRee CreateBT1(char* pre, char* in, int n)
{
BTNode* s; char* p; int k;
if (n <= 0) return NULL;
s = new BTNode;
s->data = *pre; //创建根节点
for (p = in; p < in + n; p++) //在中序中找为*ppos的位置k
if (*p == *pre)
break;
k = p - in;
s->lchild = CreateBT1(pre + 1, in, k);//构造左子树
s->rchild = CreateBT1(pre + k + 1, p + 1, n - k - 1);//右子树
return s;
}
- 已知后序和中序遍历序列构造二叉树
根据后序遍历确定根节点(最后一个)
然后根据中序遍历确定左子树和右子树
BTRee CreateBT2(char *post,char *in,int n)
{ BTNode *s; char *p; int k;
if (n<=0) return NULL;
s=new BTNode;//创建节点
s->data=*(post+n-1); //构造根节点。
for (p=in;p<in+n;p++)//在中序中找为*ppos的位置k
if (*p==*(post+n-1))
break;
k=p-in;
s->lchild=CreateBT2(post,in,k); //构造左子树
s->rchild=CreateBT2(post+k,p+1,n-k-1);//构造右子树
return s;
}
- 层次遍历法建二叉树
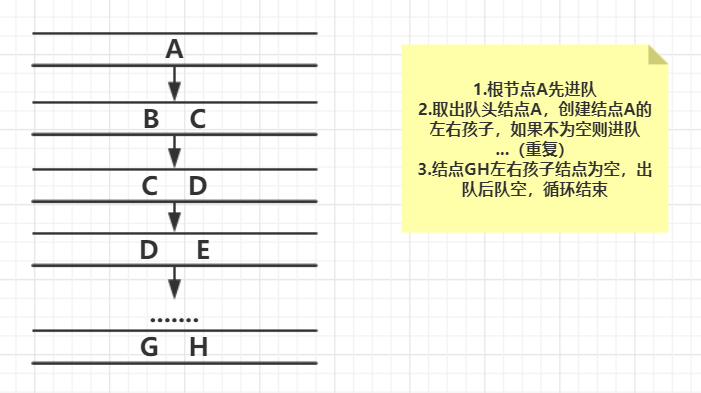
思路:
取字符串第一个数据,创建根结点,入队列
while(队列不空)
{ 出队一个节点T
取一个字符str[i]
if(str[i]=='0') T->lchild=NULL
else 生成T的左孩子,值str[i],并把左孩子入队列。
取一个字符str[i]
if(str[i]=='0') T->rchild=NULL
else 生成T的右孩子,值str[i],并把右孩子入队列。
}
代码:
void CreateBTree(BTree& BT, string str)
{
BTree T; int i = 0;
queue<BTree> Q;//队列
if (str[0] != '0') { /*分配根结点单元,并将结点地址入队*/
BT = new BTNode;
BT->data = str[0];
BT->lchild = BT->rchild = NULL;
Q.push(BT);
}
else BT = NULL; /* 若第1个数据就是0,返回空树 */
while (!Q.empty())
{
T = Q.front();/*从队列中取出一结点地址*/
Q.pop();
i++;
if (str[i] == '0') T->lchild = NULL;
else
{ /*生成左孩子结点;新结点入队*/
T->lchild = new BTNode;
T->lchild->data = str[i];
T->lchild->lchild = T->lchild->rchild = NULL;
Q.push(T->lchild);
}
i++; /* 读入T的右孩子 */
if (str[i] == '0') T->rchild = NULL;
else
{ /*生成右孩子结点;新结点入队*/
T->rchild = new BTNode;;
T->rchild->data = str[i];
T->rchild->lchild = T->rchild->rchild = NULL;
Q.push(T->rchild);
}
} /* 结束while */
}
- 括号法字符串建二叉树
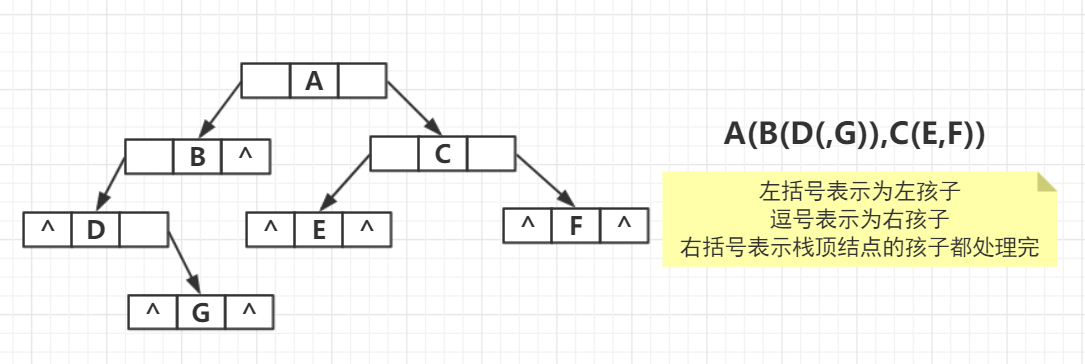
void CreateBTNode(BTNode*& b,char* str)
{ //由str二叉链b
BTNode* St[MaxSize],* p;
int top = -1, k , j = 0;
char ch;
b = NULL; //建立的二叉链初始时为空
ch = str[j];
while (ch != '\0') //str未扫描完时循环
{
switch (ch)
{
case '(': top++; St[top] = p; k = 1; break; //可能有左孩子结点,进栈
case ')': top--; break;
case ',': k = 2; break; //后面为右孩子结点
default: //遇到结点值
p = (BTNode*)malloc(sizeof(BTNode));
p->data = ch; p->lchild = p->rchild = NULL;
if (b == NULL) //p为二叉树的根结点
b = p;
else //已建立二叉树根结点
{
switch (k)
{
case 1: St[top]->lchild = p; break;
case 2: St[top]->rchild = p; break;
}
}
}
j++; ch = str[j]; //继续扫描str
}
}
1.1.4 二叉树的遍历
- 先序遍历(根左右)
访问根节点;
先序遍历左子树;
先序遍历右子树;先序遍历的递归过程为:若二叉树为空,遍历结束。否则:①访问根结点;②先序遍历根结点的左子树;③先序遍历根结点的右子树。 简单来说先序遍历就是在深入时遇到结点就访问。
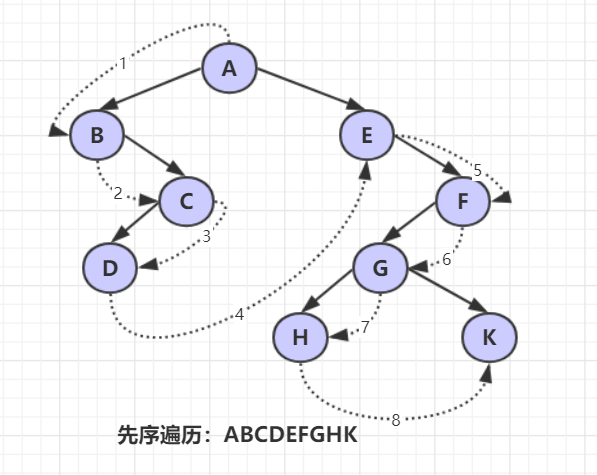
先序遍历的递归算法:
void PreOrder(BTree bt)
{ if (bt!=NULL)
{ printf("%c ",bt->data); //访问根结点
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
先序遍历非递归算法:
若二叉树bt不空,则入栈根节点bt。
while(栈不空)
{ 出栈栈顶,访问根节点。
if(bt有右孩子) 入栈bt->rchild。
if(bt有左孩子) 入栈bt->lchild。
}
- 中序遍历(左根右)
中序遍历左子树;
访问根节点;
中序遍历右子树;中序遍历的递归过程为:若二叉树为空,遍历结束。否则:①中序遍历根结点的左子树;②访问根结点;③中序遍历根结点的右子树。简单来说中序遍历就是从左子树返回时遇到结点就访问。
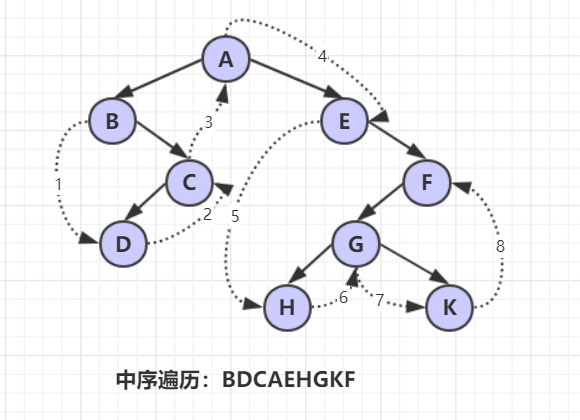
中序遍历的递归算法:
void InOrder(BTree bt)
{
if (bt!=NULL)
{
InOrder(bt->lchild);
printf("%c ",bt->data); //访问根结点
InOrder(bt->rchild);
}
}
- 后序遍历(左右根)
后序遍历左子树;
后序遍历右子树;
访问根节点;后序遍历的递归过程为:若二叉树为空,遍历结束。否则:①后序遍历根结点的左子树;②后序遍历根结点的右子树;③访问根结点。简单来说后序遍历就是从右子树返回时遇到结点就访问。
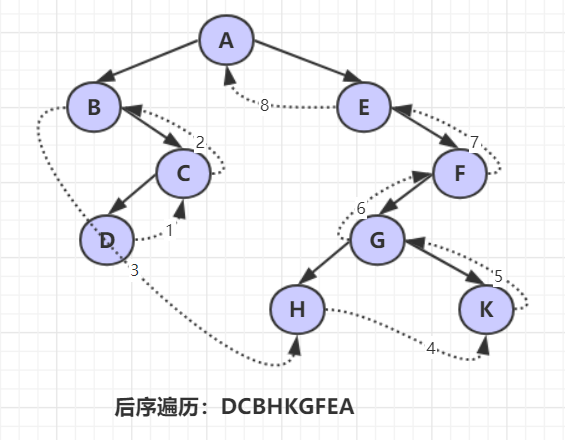
后序遍历的递归算法:
void PostOrder(BTree bt)
{
if (bt!=NULL)
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
printf("%c ",bt->data); //访问根结点
}
}
- 层次遍历
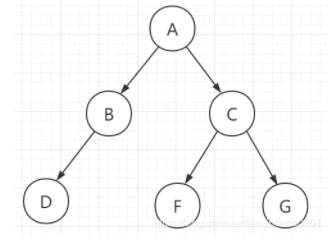
这棵二叉树的层次遍历次序为:A、B、C、D、F、G 每次出队一个元素,就将该元素的孩子节点加入队列中,直至队列中元素个数为0时,出队的顺序就是该二叉树的层次遍历结果.
void PrintTree(BTree BT)//层次遍历二叉树
{
BTree ptr;//遍历二叉树
queue<BTree>qu;
qu.push(BT);//根结点进栈
while (!qu.empty())//若队列不为空
{
ptr = qu.front();//第一个元素出栈
qu.pop();
cout << ptr->data;
if (ptr->lchild != NULL)//若出栈元素有左右子结点,进栈
qu.push(ptr->lchild);
if (ptr->rchild != NULL)
qu.push(ptr->rchild);
}
}
1.1.5 线索二叉树
在二叉树的结点上加上线索的二叉树称为线索二叉树。每个节点有两个指针域,n个结点总共有2n个指针域,非空链域为n-1个,空链域有n+1个
- 结构体定义
typedef struct node
{ ElemType data; //结点数据域
int ltag,rtag; //增加的线索标记
struct node *lchild; //左孩子或线索指针
struct node *rchild; //右孩子或线索指针
} TBTNode; //线索树结点类型定义
- 线索二叉树性质:
1)若结点有左子树,则lchild指向其左孩子;否则, lchild指向其直接前驱(即线索);
2)若结点有右子树,则rchild指向其右孩子;否则, rchild指向其直接后继(即线索) 。
为了表示有无左右孩子,增加两个标志域:
| 左孩子域 | 左孩子标志域 | 节点数据 | 右孩子标志域 | 右孩子域 |
|---|---|---|---|---|
| lchild | LTag | data | RTag | rchild |
LTag :若 LTag=0, lchild域指向左孩子; 若 LTag=1, lchild域指向其前驱。
RTag :若 RTag=0, rchild域指向右孩子; 若 RTag=1, rchild域指向其后继。
- 中序线索二叉树
中序线索二叉树可以找到对应树每个节点的前驱和后继节点。先序和后序线索二叉树无法做到。
优点:中序遍历算法既没有递归也没有用栈,所有节点只需遍历一次,空间效率得到提高。
结点的后继:(前继同理)
结点有右孩子,则为右子树最左孩子节点
结点无右孩子,则为后继线索指针指向节点
- 代码
TBTNode* pre; //全局变量
TBTNode* CreatThread(TBTNode* b) //中序线索化二叉树
{
TBTNode* root;
root = (TBTNode*)malloc(sizeof(TBTNode)); //创建头结点
root->ltag = 0; root->rtag = 1; root->rchild = b;
if (b == NULL) root->lchild = root; //空二叉树
else
{
root->lchild = b;
pre = root; //pre是*p的前驱结点,供加线索用
Thread(b); //中序遍历线索化二叉树
pre->rchild = root; //最后处理,加入指向头结点的线索
pre->rtag = 1;
root->rchild = pre; //头结点右线索化
}
return root;
}
void Thread(TBTNode*& p) //对二叉树b进行中序线索化
{
if (p != NULL)
{
Thread(p->lchild); //左子树线索化
if (p->lchild == NULL) //前驱线索化
{
p->lchild = pre; p->ltag = 1;
} //建立当前结点的前驱线索
else p->ltag = 0;
if (pre->rchild == NULL) //后继线索化
{
pre->rchild = p; pre->rtag = 1;
} //建立前驱结点的后继线索
else pre->rtag = 0;
pre = p;
Thread(p->rchild); //递归调用右子树线索化
}
}
1.1.6 二叉树的应用--表达式树
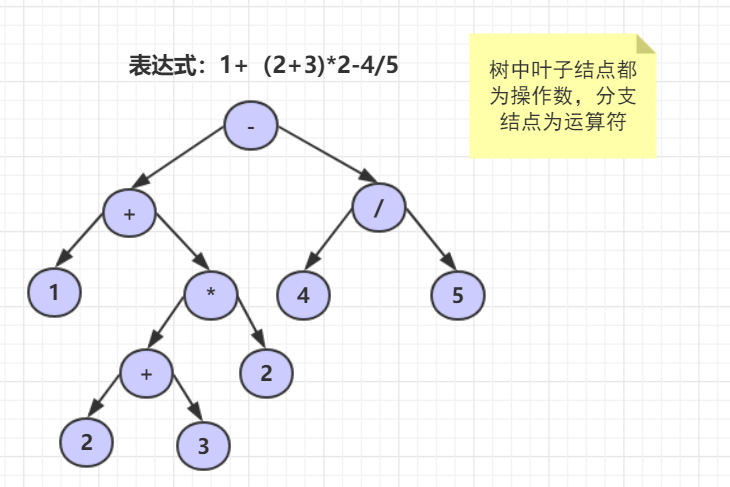
- 思路
//观察表达式树会发现数字字符的左孩子右孩子都是空的用于后面的表达式树的运算
//创建两个栈一个是树节点的保存类型一个是字符保存栈
for(int i=0;str[i];i++){
if(字符是数字)创建树节点并且入栈
else
{
if(字符栈栈顶优先级小于str[i]){
则进栈字符栈
}
else if(字符栈栈顶优先级大于str[i]){
出栈并且从节点栈中拿出两个;
构树并且放回节点栈中
}
else
直接出栈
}
计算表达式
{
if(BT->rchild==NULL&&BT->lchild==NULL)
return BT->data-'0'
else{
a=计算遍历右树
b=计算遍历左树
switch()
{
case '+':return a+b;
case '-':return a-b
case '*':returna*b
case '/':return a/b
}
}
- 代码实现
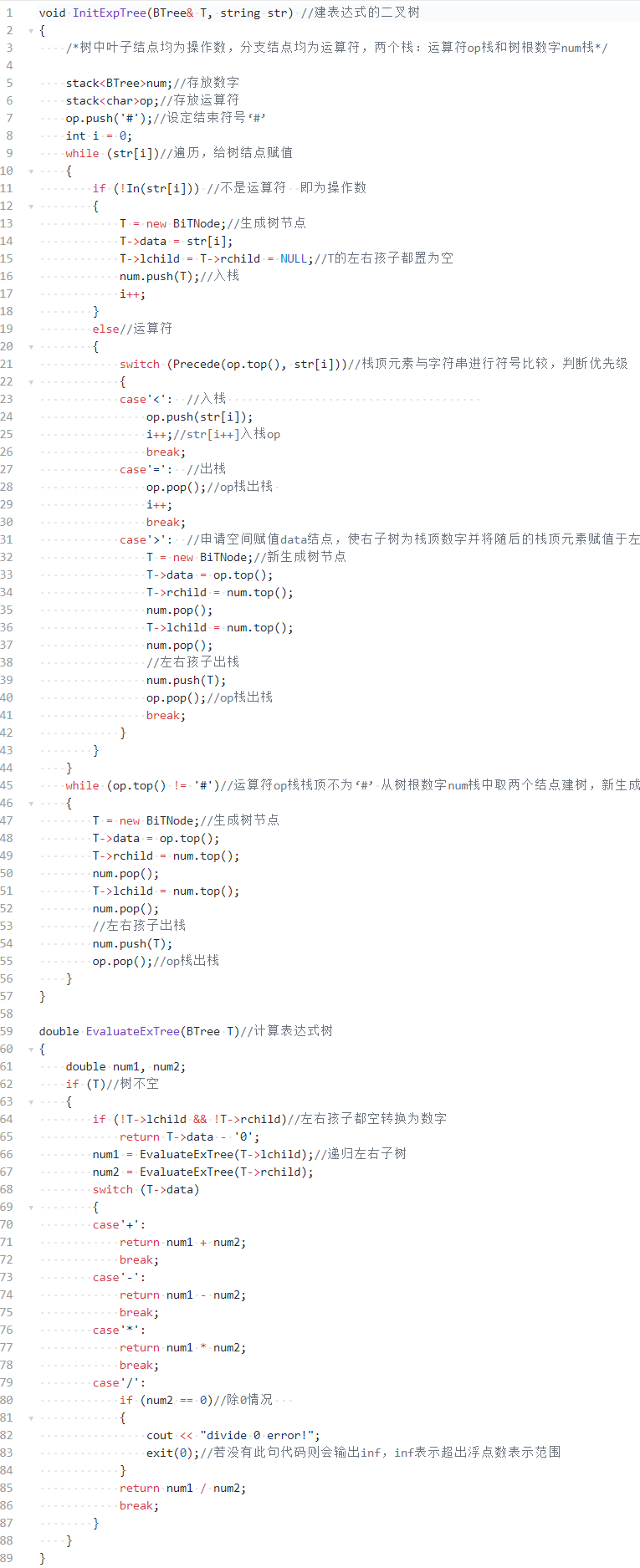
1.2 多叉树结构
定义:它是由n(n>=0)个有限结点组成一个具有层次关系的集合。
1.2.1 多叉树结构
- 双亲存储结构
结构体定义:
typedef struct
{
ElemType data; //结点的值
int parent; //指向双亲的位置
}PTree[MaxSize];
缺点:找父亲容易,找孩子不容易
- 孩子链存储结构
结构体定义:
typedef struct node
{
ElemType data; //结点的值
struct tnode *sons[MaxSons]; //指向孩子结点
}TSonNode;
缺点:空指针太多,找父亲不容易
- 孩子兄弟链存储结构
孩子兄弟链存储结构是为每个结点设计3个域:
- 一个数据元素域
- 第一个孩子结点指针域
- 一个兄弟结点指针域
结构体定义:
typedef struct tnode
{
ElemType data; //结点的值
struct tnode *son; //指向兄弟
struct tnode *brother; //指向孩子结点
}TSBNode;
每个结点固定只有两个指针域,类似二叉树,找父亲不容易
Q1:在一棵树T中最常 用的操作是查找某个结点的祖先结点,采用哪种存储结构最合适?
双亲存储结构
Q2:如最常用的操作是查找某个结点的所有兄弟,采用哪种存储结构最合适?
孩子链存储结构或者孩子兄弟链存储结构
1.2.2 多叉树遍历
树的遍历运算是 指按某种方式访问树中的每一个结点且每一个结点只被访问一次。
- 先根遍历(递归)(根左右)
若树不空,则先访问根结点,然后依次先根遍历各棵子树。
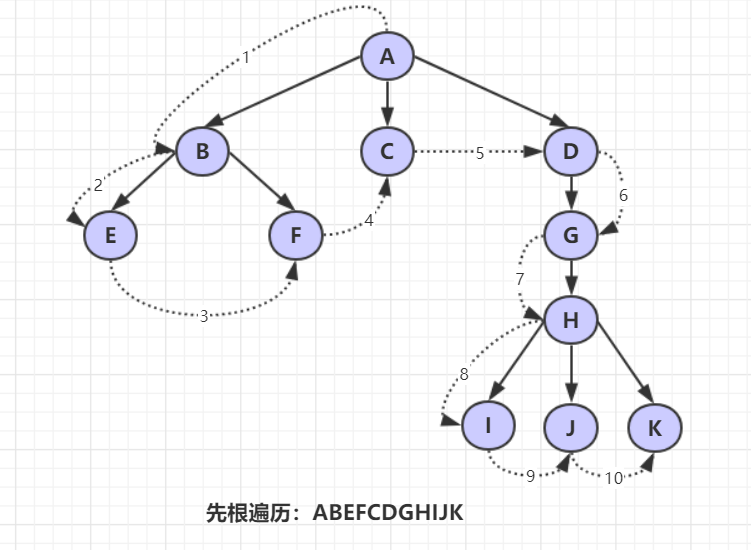
- 后根遍历(递归)(左右根)
若树不空,则先依次后根遍历各棵子树,然后访问根结点。
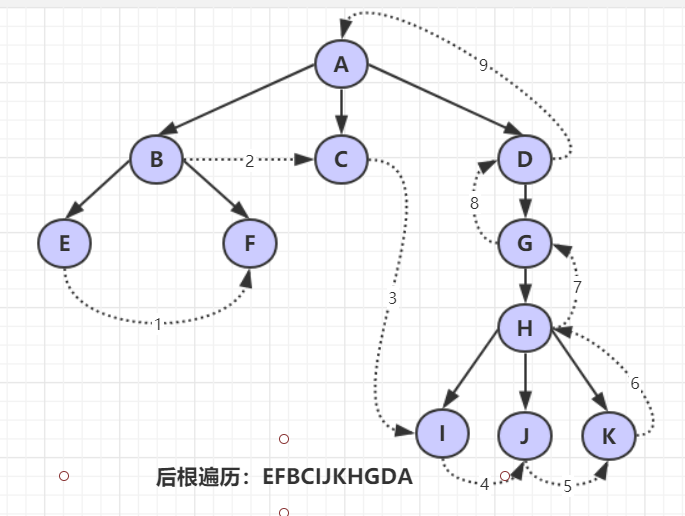
- 层次遍历
若树不空,则自上而下、自左至右访问树中每个结点。
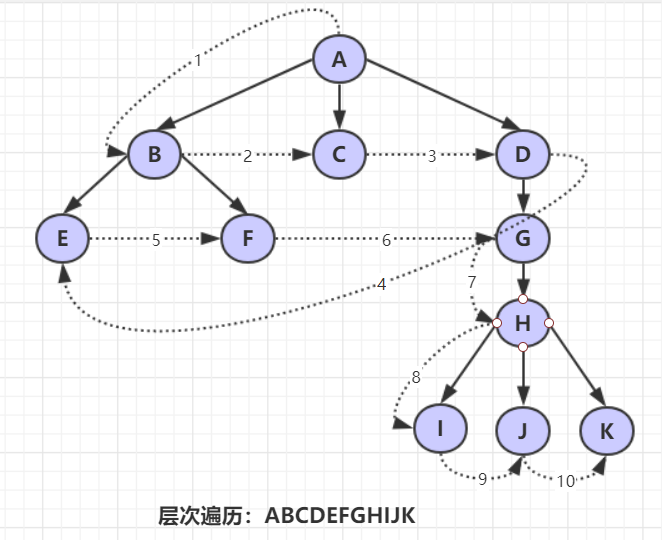
1.3 哈夫曼树
1.3.1 哈夫曼树定义
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
原则:权值越大的叶结点越靠近根结点;权值越小的叶结点越远离根结点。
WPL值->带权路径长度
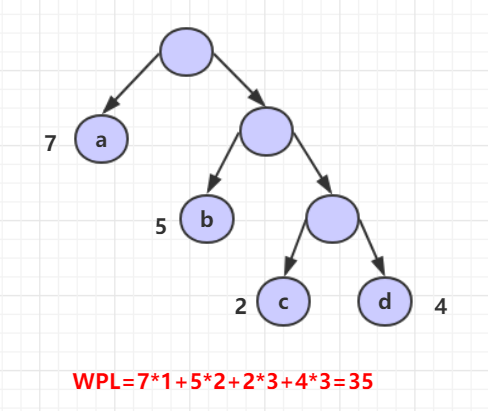
1.3.2 哈夫曼树的结构体
- 顺序结构
typedef struct
{ char data; //节点值
float weight; //权重
int parent; //双亲节点
int lchild; //左孩子节点
int rchild; //右孩子节点
} HTNode;
- 初始化哈夫曼树
typedef struct
{
int data;
int parent;
int lchild;
int rchild;
}HTNode,*HuffmanTree;
void CreateHTree(HuffmanTree &ht, int n)
{
int len;
len = 2 * n - 1;
ht = new HTNode[len];
}
1.3.2 哈夫曼树构建
- 构造哈夫曼树的过程
(1)根据给定的n个权值{w1,w2,……wn},构造n棵只有根结点的二叉树。F={T1,T2,…,Tn}。
(2)在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。
(3)在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中。
(4)重复(2)、(3)两步,当F中只剩下一棵二叉树时,这棵二叉树便是所要建立的哈夫曼树。
- 用ht[]数组构造哈夫曼树
算法思路
1.初始化哈夫曼数组ht,包含n个叶子结点,2n-1个总节点
* 所有2n-1个节点的parent、lchild和rchild域置为初值-1。
* 输入n个叶子节点有data和weight域值
2.构造非叶子节点ht[i](存放在ht[n]~ht[2n-2]中)
* 从ht[0] ~ht[i-1]中找出根节点(即其parent域为-1)最小的两个节点ht[lnode]和ht[rnode]
* ht[lnode]和ht[rnode]的双亲节点置为ht[i],并且ht[i].weight= ht[lnode].weight+ht[rnode].weight。
3.如此这样直到所有2n-1个非叶子节点处理完毕。
代码
void CreateHT(HTNode ht[],int n)
{ int i,j,k,lnode,rnode; float min1,min2;
//此处补充叶子节点相关设置
for (i=0;i<2*n-1;i++) //所有节点的相关域置初值-1
ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
for (i=n;i<2*n-1;i++) //构造哈夫曼树
{ min1=min2=32767; lnode=rnode=-1;
for (k=0;k<=i-1;k++)
if (ht[k].parent==-1) //未构造二叉树的节点中查找
{ if (ht[k].weight<min1)
{ min2=min1;rnode=lnode;
min1=ht[k].weight;lnode=k; }
else if (ht[k].weight<min2)
{ min2=ht[k].weight;rnode=k; }
} //if
ht[lnode].parent=i;ht[rnode].parent=i;
ht[i].weight=ht[lnode].weight+ht[rnode].weight;
ht[i].lchild=lnode;ht[i].rchild=rnode;
}
}
1.3.3 哈夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
- 结合一组叶子节点的数据,介绍如何构造哈夫曼树及哈夫曼编码。
- (可选)哈夫曼树代码设计,也可以参考链式设计方法。
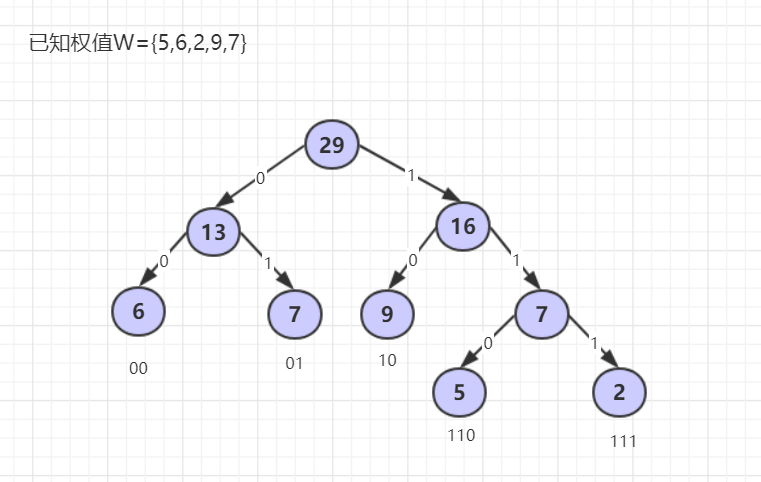
结构体
typedef struct
{ char cd[N]; //存放当前节点的哈夫曼码
int start; //哈夫曼码在cd中的起始位置
} HCode;
哈夫曼编码具体代码:
void CreateHCode(HTNode ht[],HCode hcd[],int n)
{ int i,f,c; HCode hc;
for (i=0;i<n;i++) //根据哈夫曼树求哈夫曼编码
{ hc.start=n;c=i; f=ht[i].parent;
while (f!=-1) //循环直到无双亲节点即到达树根节点
{ if (ht[f].lchild==c) //当前节点是左孩子节点
hc.cd[hc.start--]='0';
else //当前节点是双亲节点的右孩子节点
hc.cd[hc.start--]='1';
c=f;f=ht[f].parent; //再对双亲节点进行同样的操作
}
hc.start++; //start指向哈夫曼编码最开始字符
hcd[i]=hc;
}
}
1.4 并查集
并查集,在一些有N个元素的集合)应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
- 并查集解决问题
初始化:每个点看做一棵树 ,并且为每个树的树根;树根就是每个组别的代表。
查询:对于点对(a,b),通过a和b去向上查找他们的祖先节点直到树根,如果有相同的祖先节点,则他们在已经在一棵树下,属于同一组别。
合并:若不在同一组别,令其中一个点(比如a)所在树的根节点成为另一个点(比如b
)的根节点的孩子。这样即便再查询到a,最终会判断认为a属于b的组别。
大树小树合并技巧: 小树变成大树的子树,会比大树变成小树的子树更加不易增加树高,这样可以减少查询次数。
- 并查集的结构体
typedef struct node
{ int data; //结点对应人的编号
int rank; //结点秩:子树的高度,合并用
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
- 初始化并查集
void MAKE_SET(UFSTree t[],int n) //初始化并查集树
{ int i;
for (i=1;i<=n;i++)
{ t[i].data=i; //数据为该人的编号
t[i].rank=0; //秩初始化为0
t[i].parent=i; //双亲初始化指向自已
}
}
- 并查集的查找
int FIND_SET(UFSTree t[],int x) //在x所在子树中查找集合编号
{ if (x!=t[x].parent) //双亲不是自已
return(FIND_SET(t,t[x].parent)); //递归在双亲中找x
else
return(x); //双亲是自已,返回x
}
- 并查集的合并
void UNION(UFSTree t[],int x,int y) //将x和y所在的子树合并
{ x=FIND_SET(t,x); //查找x所在分离集合树的编号
y=FIND_SET(t,y); //查找y所在分离集合树的编号
if (t[x].rank>t[y].rank) //y结点的秩小于x结点的秩
t[y].parent=x; //将y连到x结点上,x作为y的双亲结点
else //y结点的秩大于等于x结点的秩
{ t[x].parent=y; //将x连到y结点上,y作为x的双亲结点
if (t[x].rank==t[y].rank) //x和y结点的秩相同
t[y].rank++; //y结点的秩增1
}
}
1.5.谈谈你对树的认识及学习体会
- 树是我们学习的第一个非线性结构,刚开始学习这个结构的时候觉得相比于线性结构来说更复杂了,但表现的形式也就更加多样。树中的许多操作都和递归有关。例如,先序遍历二叉树的代码中,虽然只有仅仅四五行的代码,但里面的递归还是有点难理解的。如果碰到在循环中的递归,代码层面上就比较难理解。
- 我们借助了树结构,建立了目录,表达式树...通过哈夫曼树,并查集,解决了更复杂的问题。知识学习的越来越多,对于我们吸收并运用的能力也在逐步加深,也需要不断理解知识。
2.PTA实验作业
2.1 jmu-ds-输出二叉树每层节点
层次遍历树中所有节点。输出每层树节点。
树结构按照树的先序遍历递归建树,比如先序遍历字符串“ABD#G###CEH###F#I##”
#代表空节点。对应树结构如下图,
输入格式:
输入一行字符串。空节点用
#表示。输出格式:
层次遍历二叉树,按照层次输出所在层及其包含节点,节点间要求
,隔开,最后一个节点尾部带,。若二叉树为空,则输出NULL输入样例:
ABD#G###CEH###F#I##输出样例:
1:A, 2:B,C, 3:D,E,F, 4:G,H,I,
2.1.1 解题思路及伪代码
解题思路
先先序遍历二叉树
再进行层次遍历,输出每层结点
但需判断是否为第一层结点
并引用node和lastnode分别用于存放遍历中途结点的孩子结点并判断是否找到这一层的最后一个结点
运用两个指针记住当前结点位置和每层的最后一个结点位置,以便于当当前结点等于层最后结点时,输出换行并输出下一层结点;而每层的结点都要通过队列依次存入并且依次输出。
伪代码
void LevelOrder(BTree bt)//层次遍历
{
定义变量层数和flag判断是否为第一层结点
BTree node, lastNode 分别用于存放遍历中途结点的孩子结点并判断是否找到这一层的最后一个结点
node = lastNode = bt;
用队列来存放结点
二叉树不为空,则出队
二叉树为空 NULL
while (!qtree.empty())//队列不空
{
若找到这一层的最后一个结点
层层递增
(格式控制输出)
取队尾元素
}
取队首元素
左右孩子入队
}
}
2.1.2 总结解题所用的知识点
- 运用了
#include <queue>库函数,将非线性结构和线性结构有效结合,借助队列的知识进行存放元素。 - 先序遍历和层次遍历
- 运用两个指针记住当前结点位置和每层的最后一个结点位置,以便于当当前结点等于层最后结点时,输出换行并输出下一层结点;而每层的结点都要通过队列依次存入并且依次输出。
2.2 目录树
输入格式:
输入首先给出正整数N(≤104),表示ZIP归档文件中的文件和目录的数量。随后N行,每行有如下格式的文件或目录的相对路径和名称(每行不超过260个字符):
- 路径和名称中的字符仅包括英文字母(区分大小写);
- 符号“\”仅作为路径分隔符出现;
- 目录以符号“\”结束;
- 不存在重复的输入项目;
- 整个输入大小不超过2MB。
输出格式:
假设所有的路径都相对于root目录。从root目录开始,在输出时每个目录首先输出自己的名字,然后以字典序输出所有子目录,然后以字典序输出所有文件。注意,在输出时,应根据目录的相对关系使用空格进行缩进,每级目录或文件比上一级多缩进2个空格。
输入样例:
7 b c\ ab\cd a\bc ab\d a\d\a a\d\z\输出样例:
root a d z a bc ab cd d c b
2.2.1 解题思路及伪代码
解题思路
- 分析题目:
本题主要分为两个子问题:一是根据输入的信息建立树,二是根据树的结构输出文件目录
- 依题意,文件树需要用左孩子右兄弟的二叉链表存储
- root是根目录,所以首先建立根节点。在扫描每一行字符串的时候,都从root开始,逐一向下将每层结点插入相应的兄弟链表中
- 结点是先序遍历输出
- 实现要点:
- 建树,需要注意输出的顺序,即同层目录排在文件前,同类按字典顺序输出
- 输出时,注意不同层结点输出不同的缩进
设计目录树,结构体 → 初始化树,新建根节点 → 建树:扫面字符串,分离文件、目录 → 插入目录树 → 输出树
- 建树的核心思路:
- 目录的插入优先级高于文件,即目录相当于非叶结点,文件相当于叶结点。所以,文件不管是否按照自带你顺序排列,和目录比它都要往后移
- 每次只处理一行字符串,都是从根节点root开始逐一插入这行的目录或文件
- 插入优先级相同的字典序在前
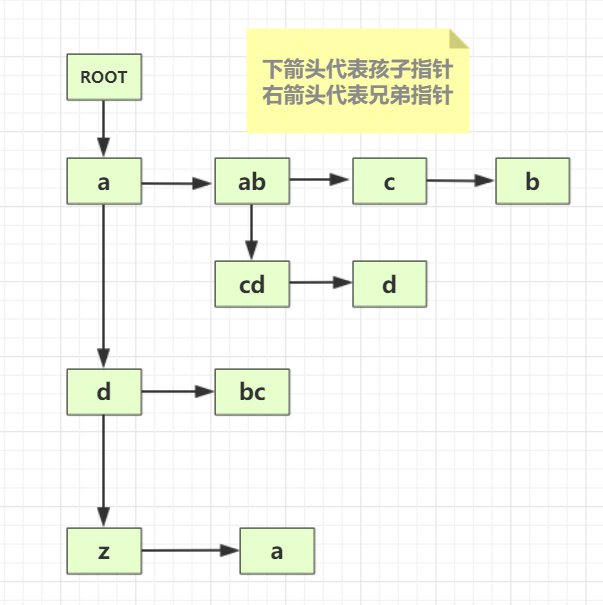
-
建树过程:
- 先建立一棵仅有根节点root的二叉树
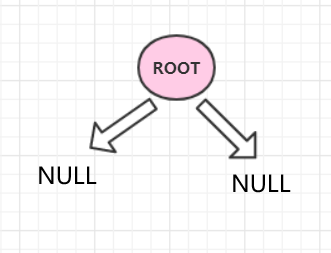
- 读入一行字符串(一行字符串可以有若干个目录但至多只有一个文件)
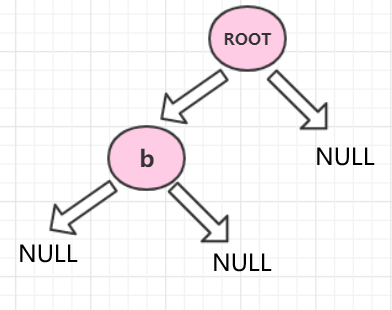
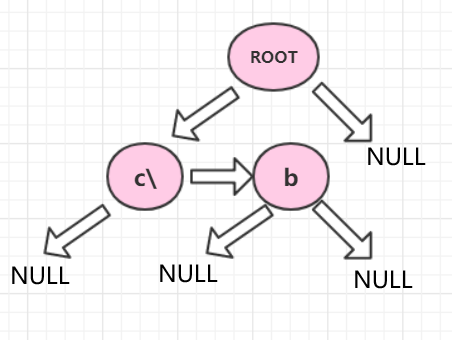
(以此类推)
-
规定
true--文件 false--目录,目录的优先级始种高于文件的优先级 -
①若待插入优先级比链上这个结点大或者优先级相同但待插入结点字典序较小的话就直接插入链上这个结点Node的前面即可
②优先级比链上这个结点小或者优先级相同但是字典序大于链上这个结点Node的话我们就继续沿着这条链往后寻找
③最极端的情况是找到了链的末尾,那么链的末尾就是我们带插入元素的位置
-
结点如何插入树?(如果该文件或目录还没有创建,那么创建的一定是其儿子节点。如果已经创建完毕了,那么插入的位置一定在该节点的左子树中查找)
-
插入作为孩子
-
没有第一个孩子,直接生成第一个孩子结点
-
有孩子,则需要判断是否需要更改孩子
①结点存在,即数据相等且目录文件相等,则不需要新建孩子结点,当前指针更改为孩子位置
②若孩子为文件内,新结点为目录。则更改孩子为新结点
③若孩子文件属性为同新结点,但是值比新结点大,则需更改当前指针
-
-
插入作为兄弟
-
没有兄弟,则插入新结点为兄弟
-
有兄弟,找新节点插入位置(实质上为有序链表)
①若新结点属性和兄弟属性相等且值大于兄弟,则继续遍历下个兄弟
②若新节点为文件,兄弟为目录,则继续遍历下个兄弟
③遍历中发现兄弟是文件,新结点是目录,退出循环
-
遍历结束,兄弟结点值和新结点值先弄个等,则不需要插入新结点,更改当前指针为兄弟
-
插入新结点,更改新结点兄弟关系,并把插入位置的前一个结点的兄弟改成新结点
-
-
伪代码
void CreatTree(Tree&bt ,string str,int i)
{
定义结构体指针temp,btr;
为temp申请空间并初始化,btr用于指向bt;
if(i>=str.size())
return;//路径遍历完毕
获取结点temp的名字
if(str[i]=='\\')
说明结点temp为目录,修改temp->isfile为true;
end if
if(temp为文件)
InitFile(temp,bt);//为文件temp在bt的孩子中找一个可插入位置
else //temp为目录
InitList(temp,bt);//为目录temp在bt的孩子中找一个可插入位置
CreatTree(temp,str,i);
}
void InitList(Tree& temp, Tree& bt)//对目录temp找一个插入位置
{
定义结构体指针btr来遍历二叉树bt
btr=bt->child;//btr先指向bt的孩子;
//对第一个兄弟结点进行判断
if(btr==NULL||btr为文件||temp->name<btr->name)//可插入
进行插入,要注意修改bt的孩子指针;
else if(temp->name == btr->name)
直接使temp指向btr;
else //开始从第二个兄弟结点查找插入位置
while(btr->brother != NULL)
if(btr->brother为文件||btr->brother->name>temp->name)
找到可插入位置,break;
else if(btr->brother->name == temp->name)
直接使temp指向btr->brother;break;
else
btr=btr->brother;//遍历下一兄弟结点
end if
end while
if(btr->brother为空||btr->brother->name!= temp->name)
进行插入操作:temp->brother=btr->brother;btr->brother=temp;
end if
end if
}
void InitFile(Tree& temp, Tree& bt)//对文件temp找一个可插入位置
{
定义结构体指针btr来遍历二叉树bt;
btr=bt->child;//btr先指向bt的孩子;
if(btr==NULL||btr为文件&&btr->name>=temp->name)//对第一个兄弟结点进行判断
进行插入,注意修改bt的孩子指针
else //从第二个兄弟结点进行判断
while(btr->brother != NULL)
if (btr->brother为文件&&btr->brother->name>temp->name)
找到可插入位置,break;
else
btr = btr-> brother;//遍历下一个兄弟结点
end if
end while
对temp进行插入操作:temp->brother=btr->brother;btr->brother=temp;
end if
}
2.2.2 总结解题所用的知识点
- 结点插入树,分为孩子和兄弟,采用孩子兄弟链
- 首先建立目录树。将输入的每个字符串插入到已有的目录树中,插入时将字符串的前缀与目录树的结点一层一层往下匹配,失配时创建新的目录和文件
- 后序遍历目录树,对每个结点的子目录和子文件进行排序
- 先序遍历进行输出。
3.阅读代码
3.1 题目及解题代码
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],3
/
9 20
/
15 7
返回锯齿形层序遍历如下:[
[3],
[20,9],
[15,7]
]
- 解题代码
class Solution {
public:
// 层序遍历
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if(root == NULL) {
return {}; // 双端队列
}
queue<TreeNode*> q;
q.push(root);
vector<vector<int>> ans;
bool level = false;// root 先左到右
while(!q.empty()) {
int size = q.size();
deque<int> d;
for(int i = 0; i < size; i++) {
TreeNode* node = q.front();
q.pop();
if(!level) {
d.push_back(node -> val);
}
else {
d.push_front(node -> val);
}
if(node -> left != NULL) {
q.push(node -> left);
}
if(node -> right != NULL) {
q.push(node -> right);
}
}
level = !level;
ans.push_back(vector(d.begin(), d.end()));
}
return ans;
}
};
3.2 该题的设计思路及伪代码
- 解题思路
根据题目可以知道,它所给的树的序列,左子树比根节点小,右子树比根节点大,三者都小于双亲结点,如果按照中序来看,就是从小到大的有序序列,所以说,按照中序数到对应的树节点即可。类似于层次遍历,但是不同的是,它需要转变方向。用两个栈,先存一层到一个栈中,然后这个栈的节点出栈,在输出之后,把它的孩子存入另外一个栈中。
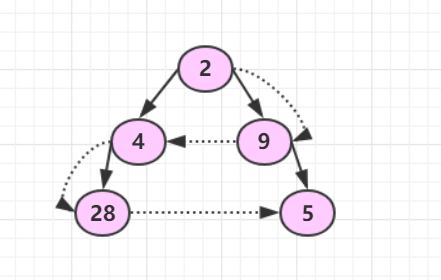

时间复杂度:有两个栈,O(2n);
空间复杂度:如果树每层最大结点树m且为2个栈,O(2m);
- 伪代码
定义两个栈s1,s2
判断树是否为空,为空直接返回
将树的根节点入s1栈
while s1或s2中有一个不为空
while s1不为空
取s1栈顶,然后出栈栈顶元素,并将其输出,(代码中是存入输出序列out)
如果这个栈顶左子树不空,将左子树入s2栈;右子树也一样
end while
(参考代码中在这输出了out)
while s2不为空
与上述操作一样,不过是存入栈s1中
end while
end while
3.3 分析该题目解题优势及难点
- 优势:与我们所学过的层次遍历类似相关,比较容易想到解题思路,另一方面可以利用我们所学的栈和队列辅助解题
- 难点:一层转换另一层是个难点