DS博客作业02--栈和队列

这个作业属于哪个班级 数据结构--网络2011/2012
这个作业的地址 DS博客作业02--栈和队列
这个作业的目标 学习栈和队列的结构设计及运算操作

目录

0.PTA得分截图

1.本周学习总结

1.1 栈

栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。无论是顺序栈还是链栈都少不了建栈，进栈，出栈，取栈顶元素，判断栈是否为空。

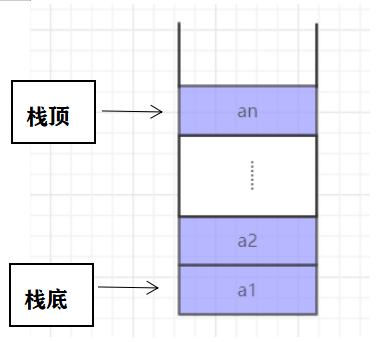
1.1.1顺序栈

在内存中用一组地址连续的存储单元依次存放从栈底到栈顶的元素。top指针位于栈顶，base指针位于栈底

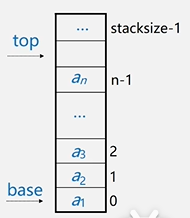
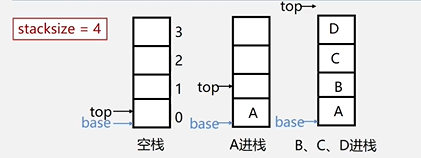
  • 定义：类比数组，栈顶就是数组的最后一个元素，只能对最后一个元素进行删除，或者在最后一个元素后面增添
typedef struct 
{  ElemType data[MaxSize]； //栈中数据元素
   int top；		//top为栈顶指针
} Stack；
typedef Stack *SqStack;

基本操作：

  • 初始化
void InitStack(SqStack s)
{
    s = new SqStack;//分配一个顺序栈的空间，首地址存放s处
    s->top = -1;    //栈顶指针置为-1
}

可知顺序栈判断栈空的条件为：return(s->top==-1);

  • 进栈
bool Push(SqStack &s,ElemType e)
{
    if(s->top == MAXSIZE - 1)    //判断是否栈满
    {
        return false;
    }
    s->data[s->top++] = e;    //入栈
    return true;
}
  • 出栈
bool Pop(SqStack &s,ElemType e)
{
    if(StackEmpty(s))    //判断是否为空栈
    {
        return false;
    }
    e = s->data[s->top--];    //退栈
    return true;
}
  • 取栈顶元素
bool GetTop(SqStack *s,ElemType &e)
{	
　  if (s->top==-1)	//判断栈空 
    return false;
    e=s->data[s->top];//栈顶元素赋值为e
    return true;
}
  • 判断栈空
bool StackEmpty(SqStack s)
{
    if(s->top == -1) //栈为空返回true
    {
        return true;
    }
    return false;
}
  • 判断栈满
int FullStack(SqStack s)
{
	if (s->top == MaxSize-1)
		return true;
	else
		return false;
}
  • 销毁栈
void DestroyStack(SqStack s)
{
   delete s;
}
  • 顺序栈四大要素：
  1. 栈空的条件：s->top==-1
  2. 栈满的条件：s->top==MaxSize-1
  3. 元素e的进栈操作：①将栈顶指针top+1 ②将元素e放在栈顶指针处
  4. 出栈操作：①将栈顶指针top处的元素取出放在e中 ②将栈顶指针top-1

1.1.2链栈

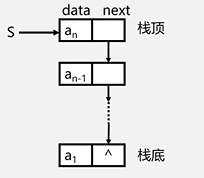
  • 定义
typedef struct StackNode
{
    ElemType data;
    struct StackNode *next;
}Node,*Stack;

基本操作：

  • 初始化
bool InitStack(Stack &s)
{
    s = NULL;
    return true;
}
  • 进栈

void Push(Stack& s, ElemType e)
{
	Stack p;
	p = new Node;
	p->data = e;		//新建节点p
	p->next = s->next;	//插入*p节点作为开始节点
	s->next = p;
}

链栈不需要考虑栈满的情况

  • 出栈

bool Pop(Stack& s, ElemType& e)
{
	Stack p;
	if (StackEmpty(s))		//栈空的情况
		return false;
	p = s->next;			//p指向开始节点，从栈顶开始出栈
	e = p->data;
	s->next = p->next;		//删除*p节点
	delete p;				//释放*p节点
	return true;
}
  • 取栈顶元素

bool GetTop(SqStack &s,ElemType e)
{
    if(StackEmpty(s))    //判断是否为空栈
    {
        return false;
    }
    e = s->data;    //取栈顶
    return true;
}
  • 判断栈空
bool StackEmpty(Stack *s)
{
    if(s == NULL)
    {
        return true;
    }
    return false;
}
  • 销毁栈
void DestroyStack(Stack &s)
{　
   Stack p;
   while (s!=NULL)
   {   p=s; 	
       s=s->next;
       delete p; 
   }
 }
  • 链栈四大要素：
  1. 栈空的条件：s->next==NULL
  2. 栈满的条件：不需考虑
  3. 元素e的进栈操作：①新建一个结点存放元素e且p指向它 ②结点p插入到头结点之后
  4. 出栈操作：取出首结点data并将其删除

1.1.3 栈的应用

  • C++模板类：stack类
#include <stack>

stack<int>s:初始化栈，参数表示元素类型

s.push(t):入栈元素t

s.top():返回栈顶元素

s.pop():出栈操作删除栈顶元素，不返回该元素

s1.empty():当栈空时，返回true

s1.size():访问栈中的元素个数
  • 表达式转换

解题思路：从头到尾读取中缀表达式的每个对象，对不同对象按不同的情况处理。

1.运算数：直接输出，但这里的数字存在小数、负数、正数。

关于正负号与数字一起输出有两种特殊情况

第一种是正负号在第一位，例如：-1+2-1，此时负号要连着数字一起输出，而如果第一位是正的则不用。

第二种是左括号连着正负号，例如：1+（-2-1）或者2+(+5)-1，此时左括号后的负号也要连着输出，而左括号后的正号则不用

2.左括号：压入栈中

3.右括号：将栈顶的运算符弹出并输出，直到遇到左括号（出栈，不输出）

4.运算符：

若优先级大于栈顶运算符时，则把它压栈；

若优先级小于等于栈顶运算符时，将栈顶运算符弹出并输出；再比较新的栈顶运算符，直到该运算符大于栈顶运算符优先级为止，然后将该运算符压栈

5.若各对象处理完毕，则把堆栈中存留的运算符一并输出

if ((exp[i] >= '0' && exp[i] <= '9') || exp[i] == '.')//如果是负数或者小数点直接输出
	 //判断是否为第一个数字，前一个是符号位，是小数点，前一个数为数字
	 
		else if (exp[i] == '+' || exp[i] == '-')//正负号
		{
			if (exp[i] == '-' && (i == 0 || exp[i - 1] == '('))//不是运算符：负号
				
			else if (exp[i] == '+' && (i == 0 || exp[i - 1] == '('))//不是运算符：是正数但不输出+号
			else//是运算符
		}
		else if (exp[i] == '*' || exp[i] == '/')//乘除号
			
		else if (exp[i] == '(')//左括号
		
		else if (exp[i] == ')')//右括号
  • 符号配对

解题思路：输入一串字符串，包括[],{},()等 来进行配对，所以把左括号存进栈里，如果是右括号则进行配对，如果不配对则返回配对失败的元素，如果最后栈为空则匹配成功，否则返回栈顶元素

伪代码：
string str;cin>>str;
strlen=str.size();
for i=0 to strlen-1
 if str[i]是左括号 则入栈 
 end if
 if str[i]是右括号
    if 栈不为空且与栈内元素匹配时
     pop();
     else 匹配失败记录栈顶元素返回false
     end if
  end if
end for
if栈不为空 那么返回栈顶元素 匹配失败
else 匹配成功 返回true

1.2 队列

队列的两端都"开口"，要求数据只能从一端进，从另一端出画一个队列的图形,进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列，一定要有队头和队尾指针的结构。

1.2.1顺序队列

  • 定义
typedef struct 
{     ElemType data[MaxSize]； 
      int front,rear；      //队首和队尾指针
}Queue;
typedef Queue *SqQueue;

基本操作：

  • 初始化
void InitQueue(SqQueue &q)
{	q=new Queue;
	q->front=q->rear=-1;
}
  • 判断栈空
bool QueueEmpty(SqQueue q)
{
   return(q->front==q->rear);
}
  • 判断栈满
bool QueueFULL(SqQueue q)
{
   return(q->rear==MaxSize-1);
}

  • 进队

bool enQueue(SqQueue &q,ElemType e)
{  
    if (q->rear+1==MaxSize)	   return false;
                                       //队满上溢出
	q->rear=q->rear+1;
	q->data[q->rear]=e;
	return true;
}
  • 出队

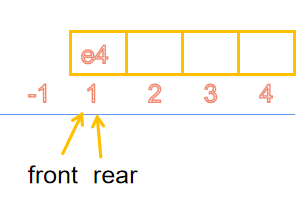
bool deQueue(SqQueue &q,ElemType &e)
{	
    if (q->front==q->rear)  //队空下溢出
	 return false;
	q->front=q->front+1;
	e=q->data[q->front];
	return true;
}
  • 销毁队列
void DestroyQueue(SqQueue &q)
{
  delete q;
}
  • 顺序队列四大要素：
    1.队空的条件：front = rear（初始时front = rear=-1）
    2.队满的条件：rear＝MaxSize－1
    3.元素e进队：rear++; data[rear]=e;
    4.元素e出队：front++; e=data[front];

1.2.2环形队列

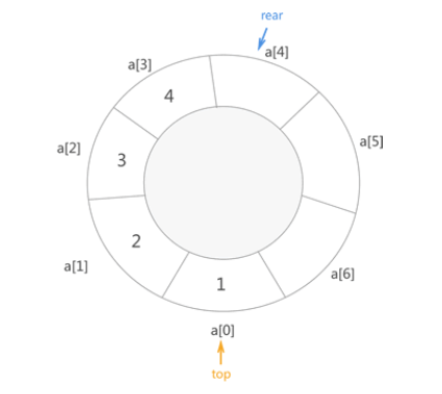
  • 定义
typedef struct 
{	
  ElemType data[MaxSize];
  int front,rear;	
} Queue;
typedef Queue *SqQueue;
  • 初始化
void InitQueue(SqQueue &q)
{   q=new Queue;
    q->front=q->rear=0;
}
  • 判断栈空
bool QueueEmpty(SqQueue q)
{
	return(q->front==q->rear);
}
  • 判断栈满
bool QueueFULL(SqQueue q)
{
	return((q->rear+1)%MaxSize==q->front);
}
  • 进队
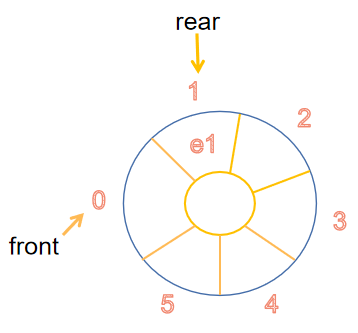
bool enQueue(SqQueue &q,ElemType e)
{	if ((q->rear+1)%MaxSize==q->front)	//队满上溢出
		return false;
	q->rear=(q->rear+1)%MaxSize;
	q->data[q->rear]=e;
	return true;
}
  • 出队

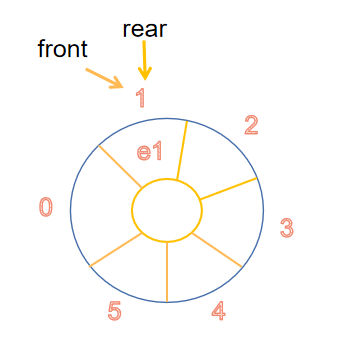
bool deQueue(SqQueue &q,ElemType &e)
{	if (q->front==q->rear)		//队空下溢出
		return false;
	q->front=(q->front+1)%MaxSize;
	e=q->data[q->front];
	return true;
}
  • 求循环队列长度
int  QueueLength (SqQueue Q)
{
     return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;                   
}

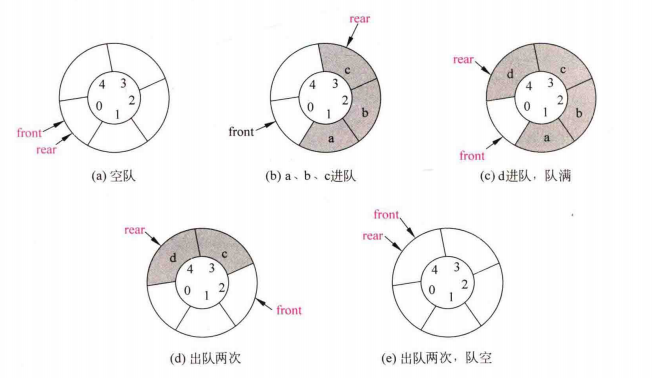
  • 环形队列四大要素

1.队空的条件：front = rear=0
2.队满的条件：(rear+1)%MaxSize=front
3.元素e入队：rear=(rear+1)%MaxSize data[rear]=e;
4.元素e出队：front=(front+1)%MaxSize data[front]=e;

  • 若已知队头指针和队列中元素的个数

1.队尾的条件：rear=(front+count)%MaxSize

2.队空的条件：count==0
3.队满的条件：count==MaxSize
4.元素e进队：先求队尾位置，队尾指针循环+1

 rear=(qu->front+qu->count)%MaxSize
 rear=(rear+1)%MaxSize
 qu->data[rear]=x;
 qu->count++;

5.元素e出队：队头指针循环+1

 qu->front=(qu->front+1)%MaxSize
 x=qu->data[qu->front];
 qu->count--;

1.2.3链队列

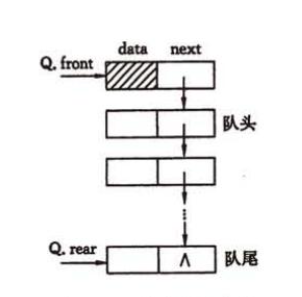
  • 定义
typedef struct QNode{
   QElemType   data;
   struct Qnode  *next;
}Qnode, *QueuePtr;//定义节点类型
typedef struct {
   QueuePtr  front;            //队头指针   
   QueuePtr  rear;             //队尾指针
}LinkQueue;  //定义队列类型
  • 初始化
Status InitQueue (LinkQueue &Q)
{
   Q.front=Q.rear=new QNode; 
    if(!Q.front) exit(OVERFLOW);
    Q.front->next=NULL;
     return OK;
}
  • 判断栈空
Status QueueEmpty(LinkQueue Q)
{
	return (Q.front == Q.rear);
}
  • 入队
Status EnQueue(LinkQueue& Q, QElemType e)
{
	p = (QueuePtr)malloc(sizeof(QNode));
	if (!p) exit(OVERFLOW);
	p->data = e; p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}
  • 出队
Status DeQueue(LinkQueue& Q, QElemType& e)
{
	if (Q.front == Q.rear) return ERROR;
	p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p) Q.rear = Q.front;
	delete p;
	return OK;
}
  • 取队头元素
Status GetHead(LinkQueue Q, QElemType& e) 
{
	if (Q.front == Q.rear) return ERROR;
	e = Q.front->next->data;
	return OK;
}
  • 销毁队列
Status DestroyQueue(LinkQueue& Q)
{
	while (Q.front)
	{
		Q.rear = Q.front->next;
		free(Q.front);
		Q.front = Q.rear;
	}
	return OK;
}
  • 链队列四大要素：
    1.队空条件：front=rear
    2.队满条件：不考虑
    3.进队e操作：将包含e的节点插入到单链表表尾
    4.出队操作：删除单链表首数据节点

1.2.4队列的应用

  • C++模板类：queue类
#include <queue>

q1.push(x):在末尾加入一个元素

q1.pop():删除第一个元素     （先取对头再pop）

q1.front():取队头元素

q1.back():取队尾元素

q1.empty():当队列空时，返回true

q1.size():访问队列中的元素个数
  • 报数游戏①

先自定义一个队列，队列存放n个数相当于报数。然后按规矩每到第m个输出并剔除一个，继续报数，直到m>n跳出循环，输出队列剩下的。

伪代码：
目标第m个 共有n个
初始化一个队列 然后赋值
if m>n return 0;
for i=0 to n
  if i==m
  cout << q.top()
  q.pop();
  else
  q.push(q.top());
  q.pop();
  end if
end for
  • 报数游戏②
n个人站成一排，从左到右编号分别为1--n，现从左到右报数“1，2，1，2...”，数到1的人出列，数到“2”的立即站到队伍最右端，报数过程反复进行，直到n个人都出列为止
初始顺序 1 2 3 4 5 6 7 8
出列顺序 1 3 5 7 2 6 4 8

伪代码：
（环形队列存储结构）
初始化队列，n个人先进队列
while(队列不空)
    出队一个元素，输出其编号
    若队列不空，再出队一个元素，该元素入队。(数到2的人继续入队)
    
    
代码：
#include<iostream>
#include<queue>
using namespace std;
int main()
{
    int i;
    int n=8;
    queue<int>q1;//初始化队列
    for(i=1;i<=n;i++)
       q1.push(i);//入队列
    while(!q1.empty())//判断队列是否为空，是返回true
    {
       cout<<q1.front()<<" ";
       //获取队首元素，访问队尾元素q1.back()
       q1.pop();
       if(!q1.empty())
       {
         front=q1.front();
         q1.pop();//出队列，不返回元素
         q1.push(q1.front());
       }
    }
    return 0;
}
  • 舞伴问题

分成男女两队，分别进队，在队列不空的情况下，分别出队

伪代码：
int QueueLen(SqQueue Q)//队列长度 
{
	因为是顺序队列，所以队列长度为队尾减队首
	返回Q->rear - Q->front;
}
int EnQueue(SqQueue& Q, Person e)//加入队列 
{
	if 队满
	返回0
	else
	元素e入队，队尾后移
}
int QueueEmpty(SqQueue& Q)//队列是否为空 
{
	直接返回队首队尾相等比较的结果
	return Q->front == Q->rear;
}
int DeQueue(SqQueue& Q, Person& e)//出队列 
{
	if 队空
	返回0
	else
	元素e出队，队首后移
}
void DancePartner(Person dancer[], int num) //配对舞伴 
{
	int k;
	Person e;
	for k = 0 to k=num-1
		if 字符数组元素为男
			元素入Fdancers队
		else 字符数组元素为女
			元素入Mdancers队
		end if
	end for
	while 男队女队都不空
		输出男女配对舞伴
	end while
}

1.3 栈和队列的区别

栈 队列
先进后出 先进先出
出栈元素在栈中完全删除 出队元素在队中不完全删除
只能在一端插入删除 在队头删除队尾插入
线性结构 线性结构
插入删除时间复杂度O(1) 插入删除时间复杂度O(1)

2.PTA实验作业

符号配对
银行业务队列简单模拟

2.1 符号配对

请编写程序检查C语言源程序中下列符号是否配对：/*与*/、(与)、[与]、{与}。

输入格式:

输入为一个C语言源程序。当读到某一行中只有一个句点.和一个回车的时候，标志着输入结束。程序中需要检查配对的符号不超过100个。

输出格式:

首先，如果所有符号配对正确，则在第一行中输出YES，否则输出NO。然后在第二行中指出第一个不配对的符号：如果缺少左符号，则输出?-右符号；如果缺少右符号，则输出左符号-?。

输入样例1：

void test()
{
    int i, A[10];
    for (i=0; i<10; i++) /*/
        A[i] = i;
}
.

输出样例1：

NO
/*-?

输入样例2：

void test()
{
    int i, A[10];
    for (i=0; i<10; i++) /**/
        A[i] = i;
}]
.

输出样例2：

NO
?-]

输入样例3：

void test()
{
    int i
    double A[10];
    for (i=0; i<10; i++) /**/
        A[i] = 0.1*i;
}
.

输出样例3：

YES

2.1.1 解题思路及伪代码

解题思路：

首先就是把串全部读进来，合成一个大串，只保留括号即可。

然后再对新生成的串处理，读入左括号，直接压入栈顶。

如果读入的是右括号：

1.如果栈为空，那么缺少与之对应的左括号。、

2.如果栈顶元素与之不匹配，那么缺少与栈顶元素相匹配的右括号。

处理完之后，如果栈为空，则表示完全匹配，如果有剩余，那么就是缺少右括号。因为是输出第一个缺少的，所以直接输出栈尾的元素就可以。

伪代码：

int CheckBracket(stack<char>& p, char str[100]);//寻找左括号
for  i=0 to length
  if (str[i] == '(' || str[i] == '[' || str[i] == '{')//左括号
        入栈
  else if (str[i] == '/' && str[i + 1] == '*')
        入栈
	    i++;//同时判断两个符号，下标要多移一位
  else if (str[i] == '*' && str[i + 1] == '/')
      //判断右边符号是否匹配
        i++;//同时判断两个符号，下标要多移一位
  else if (str[i] == '*' && str[i - 1] != '/' && str[i + 1] != '/')
          
  else
         flag = MatchBracket(p, str[i]);
         
int MatchBracket(stack<char>& p, char bot)//判断右边符号是否与栈顶元素匹配
if (bot == ')' || bot == ']' || bot == '}' || bot == '*')
	{
		if (p.empty())//栈空
		{
			cout << "NO" << endl;//缺少左括号
			if (bot == '*')
				cout << "?-" << "*/" << endl;
			else
				cout << "?-" << bot << endl;
			return -1;
		}
		else
		{
			switch (bot)
			{
			case')':
				if (栈顶== '(')//匹配成功
					出栈
				else
					cout << "NO" << endl;
					if 缺少左括号
					...
			case']':
				if (栈顶== '[')//匹配成功
					出栈
				else
					cout << "NO" << endl;
					if 缺少左括号
					...

			case'}':
			if (栈顶== '{')//匹配成功
					出栈
				else
					cout << "NO" << endl;
					if 缺少左括号
					...
			case'*':
			if (栈顶== '*')//匹配成功
					出栈
				else
					cout << "NO" << endl;
					if 缺少左括号
					...;
		      }
		 }

2.1.2 总结解题所用的知识点

1.结束符标志没有判断清除，题目是说某行只有’.’和回车才结束，也就是说如果有其他符号就不结束，而我只判断了’.’号，遇到’.’就会立马结束。
2.在判断/*符号时，应该将下标i++,同时判断两个符号，下标要多移一位,需要同时遍历。
3.调用函数之后，只针对匹配右括号进行处理，没有在开头处理。在测试点3中，开头有多余的左符号测试点一直没有过，后面在主函数后增加了条件判断。

2.2 银行业务队列简单模拟

设某银行有A、B两个业务窗口，且处理业务的速度不一样，其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时，B窗口处理完1个顾客。给定到达银行的顾客序列，请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔，并且当不同窗口同时处理完2个顾客时，A窗口顾客优先输出。

输入格式:

输入为一行正整数，其中第1个数字N(≤1000)为顾客总数，后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务，为偶数的顾客则去B窗口。数字间以空格分隔。

输出格式:

按业务处理完成的顺序输出顾客的编号。数字间以空格分隔，但最后一个编号后不能有多余的空格。

输入样例:

8 2 1 3 9 4 11 13 15

输出样例:

1 3 2 9 11 4 13 15

2.2.1 解题思路及伪代码

解题思路：

用A,B两个队列分别存储顾客编号。A存储顾客编号为奇数的，则B存储顾客号为偶数。当A窗口没有解决完2个顾客的时且A队列不空，则A出队；当A解决完2人且B队列不空，则B出队

伪代码：

for i=0 to n
   遍历入队输入顾客的编号
   if  num为偶数
     进A队
   else
     进B队
for i=0 to n
   j++//变量表示A中解决的人数
   while（j<2）
    if A不空
      取A的队首元素，出队
       //控制格式输出
   if B不空
     取B的队首元素，出队
       //控制格式输出

2.2.2 总结解题所用的知识点

1.采用queue库函数更加便捷，获取队首元素
2.需要借用flag来判断空格的输入输出
3.当A或B两个有一个队列为空就退出循环，然后单独输出不为空的队列

3.阅读代码

3.1 题目及解题代码

给定 pushed 和 popped 两个序列，每个序列中的 值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false 。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

提示：

0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。

  • 解题代码
class Solution {
public:
          bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
          stack<int >  a;
          int sizePush=pushed.size();
          int sizePop=popped.size();
          int sizePush1=0;
          int sizePop1=0;
          while (sizePush1<sizePush&&sizePop1<sizePop){
          a.push(pushed[sizePush1]);
          while(!a.empty()&&a.top()==popped[sizePop1]){//查看是否可以出栈
                 a.pop();
                 sizePop1++;
                } 
          sizePush1++;
          } 
          return a.empty();
       }
 };

3.2 该题的设计思路及伪代码

  • 设计思路：构建一个栈来表示出栈入栈的顺序。当入栈序列一一个一个入栈判断时，若栈顶为出栈序列的元素，则栈顶需要出栈，不满足就要继续压栈，一直比较到最后直到栈为空的时候，即为匹配成功。

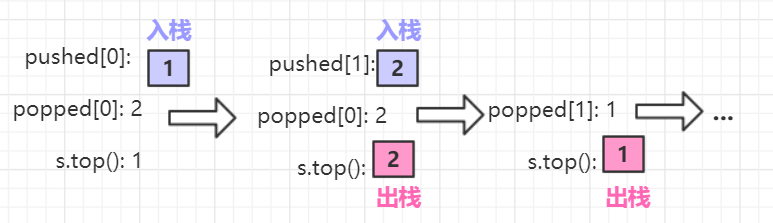
  • 时间复杂度：O(N)，其中 N 是 pushed 序列和 popped 序列的长度。
  • 空间复杂度：O(N).
  • 伪代码
stack<int> a//建立一个栈用来模拟出栈入栈
用sizePush和sizePop来记录两个序列的长度
然后用sizePush1和sizePop1来作为两个序列的下标
while(两个序列的下标都小许序列长度-1)
   让pushed[sizePush1]入栈
   while(栈顶不为空且栈顶等于popped[sizepop1])
   出栈 然后sizepop1++ //popped数组下移
   end while
   sizePush1++；不满足或者匹配成功都要继续压栈
end while
return a.empty();

3.3 分析该题目解题优势及难点。

优势：灵活运用了栈的结构特性，方法简单易懂，容易操作让序列的单独入栈与出栈序列作比较、下移，过程简单。

难点：容易出错的是什么时候压栈，有时候容易误以为压栈只有匹配不成功的时候压栈，如果匹配成功也需要压栈，同时在匹配之前一定要记得判断栈是不是为空
posted @ 2021-04-05 20:14  GGGa-Yi  阅读(179)  评论(2)  编辑  收藏  举报