DS博客作业01--线性表

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业01--线性表
这个作业的目标	学习数据结构基本概念、时间复杂度、顺序表、单链表、有序表的结构设计及运算操作
目录 0.PTA得分截图 1.1 绪论 1.1.1 数据结构有哪些结构，各种结构解决什么问题？ 1.1.2 时间复杂度及空间复杂度概念。 1.1.3 时间复杂度有哪些？如何计算程序的时间复杂度和空间复杂度，举例说明。 1.2 线性表 1.2.1 顺序表 1.2.2 链表 1.2.3 有序表 2.PTA实验作业 2.1 两个有序序列的中位数 2.1.1 解题思路及伪代码 2.1.2 碰到问题及解决方法 2.2 一元多项式的乘法与加法运算 2.2.1 解题思路及伪代码 2.2.2 碰到问题及解决方法 3.阅读代码 3.1 题目及解题代码 3.2 该题的设计思路及伪代码 3.3 分析该题目解题优势及难点。

0.PTA得分截图

1.1 绪论

1.1.1 数据结构有哪些结构，各种结构解决什么问题？

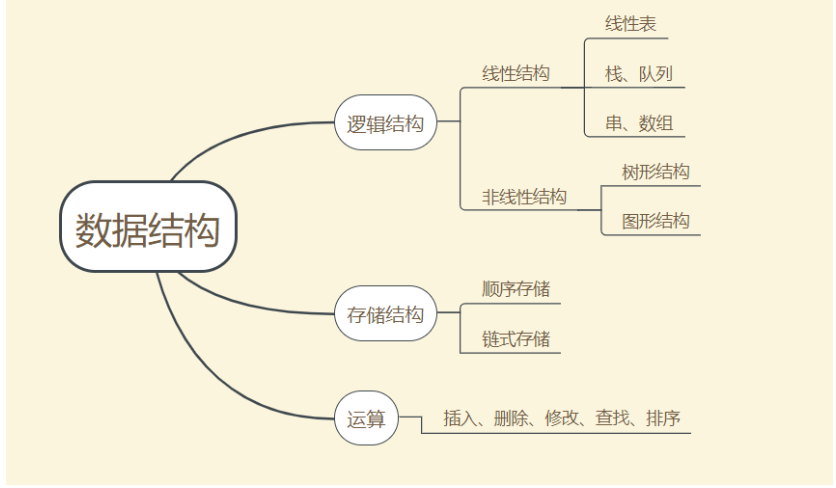
数据结构大致包含以下几种存储结构：

• 线性表，还可细分为顺序表、链表、栈和队列；
• 树结构，包括普通树，二叉树，线索二叉树等；
• 图存储结构;

线性表：具备“一对一”关系的数据就可以使用线性表来存储

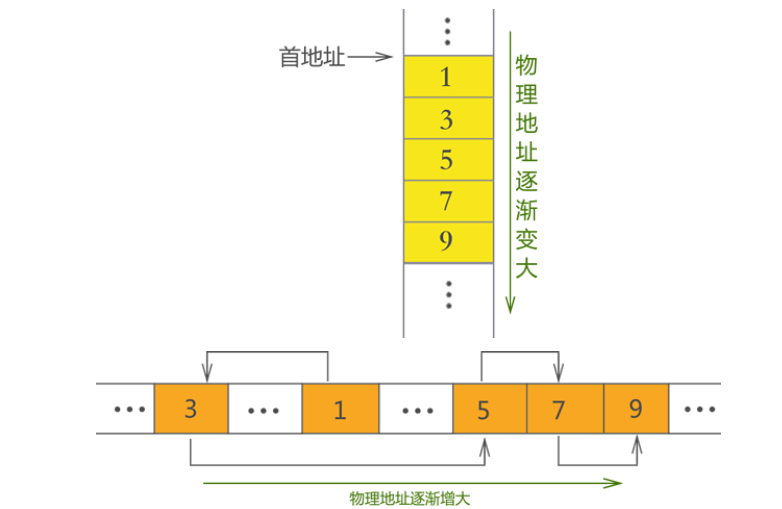
栈：中的元素只能从线性表的一端进出（另一端封死），且要遵循“先入后出”的原则，即先进栈的元素后出栈。

队列：中的元素只能从线性表的一端进，从另一端出，且要遵循“先入先出”的特点，即先进队列的元素也要先出队列。

树：存储结构适合存储具有“一对多”关系的数据。

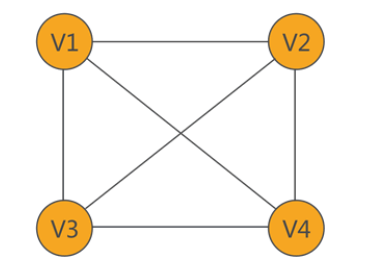
图：存储结构适合存储具有“多对多”关系的数据。

1.1.2 时间复杂度及空间复杂度概念。

• 时间复杂度

时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。即指执行算法所需要的计算工作量

• 空间复杂度

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。即指执行这个算法所需要的内存空间

1.1.3 时间复杂度有哪些？如何计算程序的时间复杂度和空间复杂度，举例说明。

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n2)平方阶 < O(n3)(立方阶) < O(2n) (指数阶)

  sum=0；                 （一次）  
    for(i=1;i<=n;i++)     （n+1次）  
      for(j=1;j<=n;j++) （n2次）  
     sum++；            （n2次）  

解：因为O(2n2+n+1)=n2,所以T(n)= =O(n2)；

for (i=1;i<n;i++)  
     {   
         y=y+1;         ①     
         for (j=0;j<=(2*n);j++)      
            x++;         ②        
     }      

解：
语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n2-n-1
f(n)=2n2-n-1+(n-1)=2n2-2；
又O(2n2-2)=n2
该程序的时间复杂度T(n)=O(n2);

  a=0;  
    b=1;                      ①  
    for (i=1;i<=n;i++) ②  
    {    
     s=a+b;　　　　③  
     b=a;　　　　　④    
     a=s;　　　　　⑤  
    }  

解：
语句1的频度：2,
语句2的频度： n,
语句3的频度： n-1,
语句4的频度：n-1,
语句5的频度：n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).

  i=1;     ①  
    While (i<=n)  
    i=i*2; ②  

解：
语句1的频度是1,
设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n
取最大值f(n)=log2n,
T(n)=O(log2n )

1.2 线性表

1.2.1 顺序表

• 顺序表结构体定义

typedef struct {
    ElementType Data[MAXSIZE];//存放线性表中的元素
    int length; // 存放线性表的长度
}SqList;

• 顺序表插入

bool Insert( List L, ElementType X, Position P ){
     Position i;
     if(L->Last==MAXSIZE-1){//当存储空间已满
     	printf("FULL");
        return false;
	 }
	if(P<0||P>L->Last+1){//插入位置错误
		printf("ILLEGAL POSITION");
		return false;
	}
	for(i=L->Last;i>=P;i--)//从最后一个元素开始
		L->Data[i+1]=L->Data[i];//插入位置及之后元素后移
		L->Data[P]=X;//将新元素e放入第i个位置
		L->Last++;//表长+1
		return true; 
}

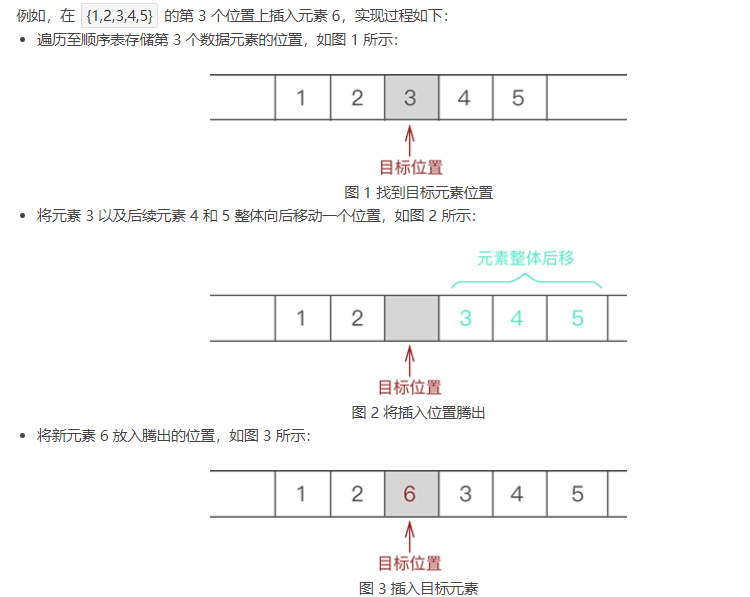
算法思想：

1. 判断顺序表存储空间是否已满
2. 判断插入位置i是否合法
3. 将第n至第i个元素一次向后移一位

需要考虑两种异常情况：插入位置是否正确 和 溢出情况

时间复杂度

• 当i=n+1，移动次数为0;

• i，移动次数n-i+1

• 当i=1,移动次数为n，达到最大值。

• 共有n+1个插入位置，概率pi=1/n+1

• 移动元素的平均次数为:
  n/2 O（n）

• 顺序表删除

bool ListDelete(List &L,int i,ElemType &e)
{  
   if (i<1 || i>L->length) //删除位置不合法
        return false;
   i--;		    //将顺序表逻辑序号转化为物理序号
   e=L->data[i];
   for (int j=i;j<L->length-1;j++)         
      L->data[j]=L->data[j+1];
   L->length--;	    //长度减1
   return true;			
}

算法思想：

1. 判断删除第i个位置是否合法
2. 将欲删除的元素保留在e中
3. 将第i+1至n个位置向前移一位
4. 表长-1

时间复杂度

• 当i=n时，移动次数为0；

• 当i=1时，移动次数为n-1。

• 假设pi是删除第i个位置上元素的概率：1/n

• 则在长度为n的线性表中删除一个元素时所需移动元素的平均次数为:
  （n-1）/2 O(n)

• 顺序存储的优缺点

优点：
1.逻辑相邻，物理相邻
2.无须为表示表中元素之间的顺序关系增加额外的存储空间
3.可随机存取任一元素
4.存储空间使用紧凑
缺点：
1.插入、删除操作需要移动大量的元素（除操作在表尾的位置进行外）
2.预先分配空间需按最大空间分配，利用不充分 
3.表容量难以扩充

1.2.2 链表

• 链表的结构体定义

typedef struct LNode  		//定义单链表结点类型
{
	ElemType data;
	struct LNode *next;		//指向后继结点
} LNode,*LinkList;        //LinkList为指向结构体LNode的指针类型

• 头插法

void CreateListF(LinkList& L, int n)//头插法建链表，L表示带头结点链表，n表示数据元素个数
{
    L = new LNode;//创建新节点
    L->next = NULL;//初始为空链表
    for (int i = 0; i < n; i++)
    {
        LNode* p = new LNode;//创建新结点
        cin >> p->data;
        p->next = L->next;//将结点s插入到原首结点之前，头结点之后
        L->next = p;//将新结点插入表中
    }
}

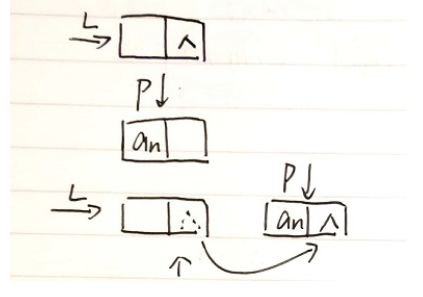
• 尾插法

void CreateListR(LinkList& L, int n)//尾插法建链表，L表示带头结点链表，n表示数据元素个数
{
    L = new LNode;//创建新节点
    L->next = NULL;//初始为空链表
    LNode* q = new LNode;
    q = L;
    for (int i = 0; i < n; i++)
    {
        LNode* p = new LNode;//创建新结点
        cin >> p->data;
        p->next=NULL;
        q->next = p;//将结点p插入到q之后
        q = p;
    }
}

• 链表插入

Status ListInsert_L(LinkList &L,int i,ElemType e)
{
  p=L;j=0;
  while(p&&j<i-1)
  {
    p=p->next;++j;//寻找第i-1个结点，p指向i-1结点
    if(!p||j>i-1)
      return ERROR;//i大于表长+1或者小于1，插入位置非法
    s=new LNode;//生成新结点s，将结点s的数据域置为e
    s->data=e;
    s->next=p->next;//将结点s插入L中
    p->next=s;
  }
}

步骤：

1. 首先找到ai-1的存储位置p
2. 生成一个数据域为e的新结点s
3. 插入新结点
   1. 将新结点的 next 指针指向插入位置后的结点；
   2. 将插入位置前结点的 next 指针指向插入结点；

• 链表删除

Status ListDelete_L(LinkList &L,int i,ElemType e)
{
  p=L;j=0;
  while(p->next&&j<i-1)
  {
    p=p->next;
    ++j;//寻找第i个结点，并令p指向其前驱
  }
  if(!(p->next)||j>i-1)
    return ERROR;//删除位置不合理
  q=p->next;//临时保存被删结点地址
  p->next=q->next;//改变删除结点前驱结点的指针域
  e=q->data;//保存删除结点的数据域
  delete q;//释放删除结点的空间
}

• 链表逆置

void ReverseList(LinkList& L)//逆转链表
{
    LNode* p, * q;//定义两个链表
    p = L->next;
    L->next = NULL;
    while (p != NULL)//不为空时逆置
    {
        q = p;
        p = p->next;
        q->next = L->next;
        L->next = q;//使用头插法将p指针后面依次插入表头L后
    }
}

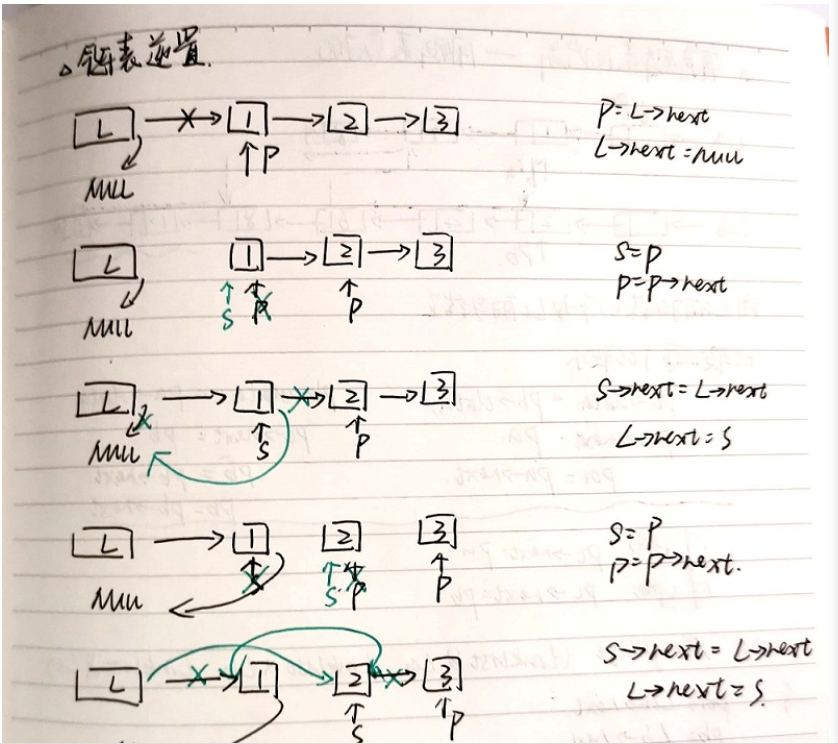
• 重构链表

p=L->next;L->next=NULL;

重构前要保护原有链的关系

• 链表操作注意事项

1、记住头节点，单链表的每个操作都要从头节点开始。如果函数内头节点发生了改变，比如在头节点之前插入节点，删除头节点，反转链表等，都需要更新头节点。否则会丢失链表。

2、遍历链表时要不断检测链表尾部。

3、插入时，需要找到插入点之前的节点。注意要特别处理在头节点之前插入时，需要更新头节点，可以通过p->next

4、删除时，考虑链表为空的情况

5、每次链表结点改变前，保存结点

6、要保留后继结点，可以设计一个新指针q=p，p=p->next

• 链表及顺序表在存储空间、插入及删除操作方面区别

	链表	顺序表
存储空间	动态分配空间，相邻数据元素可随意存放，但所占存储空间分两部分，一部分存放结点值，另一部分存放表示结点关系间的指针	空间利用率高，存取速度高效，通过下标来直接存储；但有空间限制，当元素个数远少于预先分配的空间时,空间浪费巨大
插入	效率较高，只需要改变指针指向	效率较低
删除	效率较高，只需要改变指针指向	效率较低

1.2.3 有序表

• 有序顺序表插入

void InsertSq(SqList& L, int x)
{
    int i = 0, j = 0;
    for (i = 0; i < L->length; i++)//遍历
    {
        if (x < L->data[i])//如果需要插入的数据小于表中数据则跳出循环
            break;
    }
    for (j = L->length; j > i; j--)//从最后一个元素开始
    {
        L->data[j] = L->data[j - 1];//插入位置及该位置之后的元素向后移
    }
    L->data[i] = x;//插入数据
    L->length++;//长度+1
}

• 有序单链表数据插入、删除

  思路：

需要插入元素，则需要找到插入的位置的前驱结点

需要删除元素，需要判断链表是否为空的情况

void ListInsert(LinkList& L, ElemType e)//有序链表插入元素e
{
    LinkList pre, p;
    pre=L;

    while (pre->next != NULL && pre->next->data < e)
                      //查找插入结点的前驱结点，当下一个数据小于e时
    {
        pre = pre->next;//继续遍历
    }

    p = new LNode;//新建结点
    p->data = e;//赋值
    p->next = pre->next;
    pre->next = p;

}

void ListDelete(LinkList& L, ElemType e)//链表删除元素e
{
    LinkList p, q;//循环结点
    p = L;

    if (p->next == NULL)
        return;
    while (p)
    {
        if (p->next)
        {
            if (e == p->next->data)//找到删除的元素e
            {
                q = p->next;
                p->next = q->next;
                delete q;
                return;
            }
        }
        p = p->next;//移动，继续查找要删除的元素
    }
    //遍历完，若还没有找到删除元素，则输出 x找不到！
    cout << e << "找不到！" << endl;
}

• 有序链表合并

  思路：

原本我的代码是新建了一个链表L3，且用L1的头结点作为L3的头结点进行指向。但操作相比建立一个尾指针来说，较为繁琐。而建立一个尾指针，将尾指针指向L1，指向更加明确，代码可读性也比较强。

void MergeList(LinkList& L1, LinkList L2)//合并链表
{
    LinkList P1, P2, r;//r为尾指针
	P1 = L1->next, P2 = L2->next;
	r = L1;
	L1->next = NULL;

	while (P1 && P2)
	{
		if (P1->data < P2->data)//小于
		{
			r->next = P1;
			r = P1;
			P1 = P1->next;
		}
		else if (P1->data > P2->data)//大于
		{
			r->next = P2;
			r = P2;
			P2 = P2->next;
		}
		else//等于
		{
			r->next = P2;
			r = P2;
			P1 = P1->next;
			P2 = P2->next;
		}
	}

	if (P1)
		r->next = P1;//如果未到达L1链尾，直接将P1接到链表后面
	if (P2)
		r->next = P2;//同理

}

• 有序链表合并和有序顺序表合并，有哪些优势？

	有序链表合并	有序顺序表合并
区别	可以用尾指针或者新生成一个链表结点来进行合并，只需要指针的移动，空间复杂度为O（1）	需要数据的大量移动，时间复杂度为O（m+n）

• 单循环链表特点，循环遍历方式

链表中的判别条件为p!=NULL或p->next!=NULL，而单循环链表判别条件是p!=L或p->next!=L;

在循环单链表中，找开始节点和尾节点的存储位置分别是rear->next->next(带头结点)和rear

1.循环单链表结构体定义

typedef struct Node
{
   int data;
   struct Node *next;
   
}Node,*LinkList;

2.特点

任一结点出发都可以找到表中其他结点

2.PTA实验作业

两个有序序列的中位数

一元多项式的乘法与加法运算 （未写出，未上传）

2.1 两个有序序列的中位数

已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A​0​​ ,A​1​​ ,⋯,A​N−1​​ 的中位数指A​(N−1)/2​​ 的值,即第⌊(N+1)/2⌋个数（A​0​​ 为第1个数）。

输入格式:
输入分三行。第一行给出序列的公共长度N（0<N≤100000），随后每行输入一个序列的信息，即N个非降序排列的整数。数字用空格间隔。

输出格式:
在一行中输出两个输入序列的并集序列的中位数。

2.1.1 解题思路及伪代码

解题思路

将输入的两行数字进行链表合并，合并后的链表再查找中位数

伪代码（查找中位数）

建立一个指针结构体p指向L
for i=0 to (2*n+1)/2//循环遍历，指针移动，寻找中位数
  p->next //p指向下一个元素
循环结束，即找到中位数

代码

2.1.2 碰到问题及解决方法

Q1：

循环条件是for (i = 1; i < n; i++)，中位数i的遍历条件有误

Q2：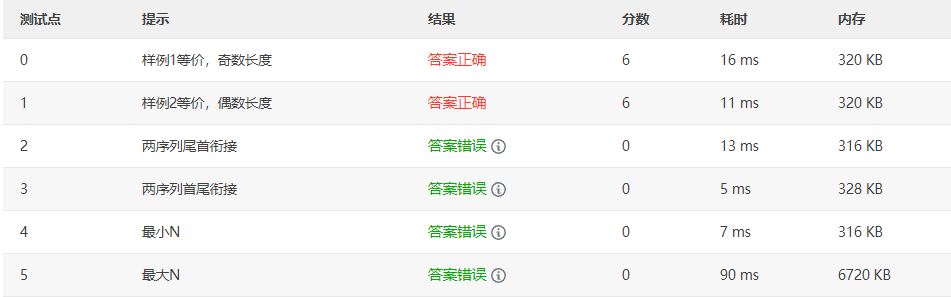

当数据相同的时候，重复数据都要写上去，所以不能P1和P2同时遍历，则链表合并数据重复时，```P1=P1->next``不能写上去

2.2 一元多项式的乘法与加法运算

设计函数分别求两个一元多项式的乘积与和。

输入格式:
输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式:
输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。

2.2.1 解题思路及伪代码

解题思路

创建多项式->多项式相加->输出链表->销毁链表
*因为是降序排列，所以多项式相加时需要采用头插法

伪代码（多项式相加）

比较指数大小，相同系数的指数合并
while（pa和pb）
   pa>pb
   
   pb>pa
   
   pa==pb

更改1：

更改2：

2.2.2 碰到问题及解决方法

3.阅读代码

3.1 题目及解题代码

• 题目

• 代码

递归：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next)   return head;
        ListNode* first = head;
        ListNode* second = head->next;
        head = second;
        first->next = swapPairs(second->next);
        second->next = first;
        return head;
    }
};

非递归：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next)   return head;
        ListNode* dummy = new ListNode(-1),*pre = dummy;
        dummy->next = head;
        while(pre->next && pre->next->next){
            ListNode*t = pre->next->next;
            pre->next->next = t->next;
            t->next = pre->next;
            pre->next = t;
            pre = t->next;
        }
        return dummy->next;
    }
};

3.2 该题的设计思路及伪代码

• 设计思路

递归：

从链表头开始把两个两个结点看成一个整体，两个结点交换后，原来第一个结点总是连接下一个的第二个结点

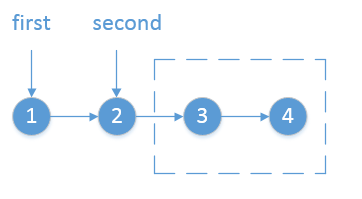
1. 交换之后2变成了头结点
2. 1要和剩下的链表进行连接
3. 最后再把2和1连接起
4. 下一次的递归式传递下一堆需要交换的结点

非递归：

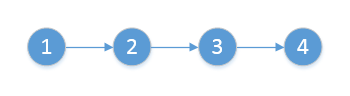
需要在最前面建立一个dummy结点的原因是当原来的头结点发生了变换，比如被删除了，或者被交换位置了，就需要记录新的头结点的位置。

首先要把结点1和3连接到一起（因为如果你先操作2和3，断开连接之后就无法到达3了）

pre->next->next = t->next;

再把2和1连接到一起

t->next = pre->next;

之后把-1和2连接到一起（因为2变成了新的头结点）

pre->next = t;

交换3，4

pre = t->next;

---

• 伪代码

if head == NULL || head->next==NULL //结束标志，递归回去的指针总是当前整体中的第一个结点；
      return head;
end if
ListNode *dummy//新建一个结点，因为原来的头结点发生变换，会断链
dummy->next=head;//指向原链的头结点
while(pre->next和pre->next->next)
    //交换列表中的前两个节点head和head.next
    ListNode *t//指向头结点的后继结点
    把第一个数和第三个数连接在一起
    再将2和1连接在一起
    再将-1和2连接(因为2成了新的头结点)
    交换3和4
end while
return dummy->next//返回

• 复杂度

	时间复杂度	空间复杂度
递归	O(N)	O(N)
非递归	O(N)	O(1)

递归次数都为n/2

3.3 分析该题目解题优势及难点。

• 优势：

  使用非递归算法是最直观的想法，思路比较简单，但还是需要画图理解。非递归算法的时间复杂度和递归算法相同，但是空间复杂度为O(1)比递归算法要小。

• 难点：

  递归算法的整个思维很巧妙且灵活，可能不会想到运用递归的方法，而且递归算法相比较还是需要理解并且画图，个人觉得递归还是有点难。