学习总结-二叉堆

ps:如果本文ppt无法正常使用，请点击这里

本文的pdf版本下载

---

(一)二叉堆的描述

习惯上，我们将二叉堆简称为"堆"。堆是由数组存储的完全二叉树，是一种实现优先队列(\(priority\) \(queue\))的数据结构。

所谓优先队列，是允许插入(\(insert\))元素，查询最优元素(最大元素或最小元素)，删除元素的三种操作。

堆在\(NOIp\) 系列竞赛中应用广泛，常用与快速查询最大(最小值)，优化各种算法(如:最短路算法)，排序......是一种效率高，应用广泛的数据结构。

(二)二叉堆的定义

这里给出堆(二叉堆)的通俗定义:

二叉堆其实就是满足如下性质的完全二叉树：对于树中的任意节点(叶子节点除外)，一定满足这个节点一定比其的两个节点更优。

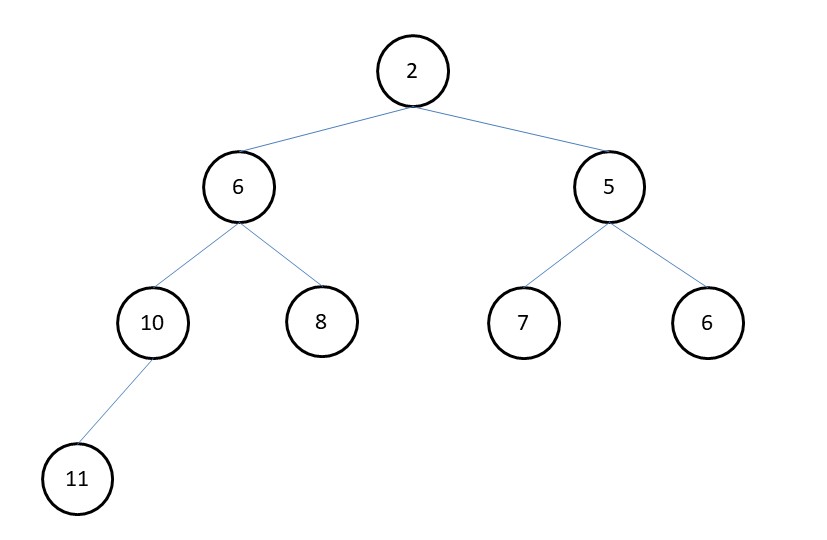
满足任意节点(叶子节点除外)都比其子节点小的二叉堆叫做小根堆(最小堆)，反之，叫做大根堆或大顶堆(最大堆)。如下图是一个小根堆。

(三)二叉堆的性质

不妨设树(堆)的高度为\(d\)，那么显然，堆具有如下性质:

1. 所有的叶子节点不是在第\(d\)层，就是在第\(d-1\)层。(完全二叉树的性质)
2. 当\(d \geqslant 1\)时，第\(d-1\)层上有\(2^{d-1}\)个节点。(完全二叉树的性质)
3. 若第\(d-1\)层上有分支节点，则这些分支节点都集中在树的最左边。(完全二叉树的性质)
4. 每个节点所存放的元素，都大于或小于它的所有子节点所存放的元素。(堆的性质)

(四)二叉堆的存储

因为上文提到过，堆是一颗完全二叉树，所以我们可以用完全二叉树的存储方式来存储堆。

即设\(q(i)\)是堆的一个节点，则它的左子节点是\(q(i\times 2)\)，右子节点是\(q(i\times 2+1)\)，它的父节点是\(q(\llcorner i\div2 \lrcorner)\) (\(\llcorner\lrcorner\)表示向下取整)。特别地，\(q(1)\)表示根节点.

(二)中的图在数组中的存储方式如下表:

下标	1	2	3	4	5	6	7	8
元素值	2	6	5	10	8	7	6	11

当将堆存储在数组中时，堆有如下性质:

1. 设该堆有\(n\)个元素，则叶子节点的下表分别为:

   \(\llcorner n/2\lrcorner+1\)，\(\llcorner n/2\lrcorner +2\)，...，n

2. 一个从小到大排好序的数组是最小堆(小根堆)，反之则不一定(因为堆的结构不唯一)

3. 一个最大堆(最小堆)中最小(最大)的元素在堆的叶子节点上。

(五)二叉堆的操作

二叉堆主要支持2种操作，为方便描述，下文的堆都是小根堆。(大根堆的操作与小根堆的类似)

代码中的部分变量名解释

\(tail:\)元素个数

\(q[\) \(]:\)堆

\(cmp(x,y):\)若\(x<y\)返回\(true\), 否则返回\(false\)

操作1:插入元素(push)

插入的基本流程是:在第\(tail+1\)个位置添加一个元素，然后再将元素上调(\(heap\) \(up\))。

上调的基本流程:

1. 若当前节点是根节点，结束循环
2. 比较当前节点与父节点的大小
   1. 若当前节点比父节点小，交换当前节点与父节点
   2. 否则结束循环
3. 将当前节点下标\(p\)变为其父节点的下标(\(\llcorner p/2 \lrcorner\))

具体操作演示见 "二叉堆插入操作.pptx"

代码段：

void heap_up(int p)
{
    while(p > 1 and cmp(q[p],q[p/2]))//如果该节点不是根节点，并且小于父节点，继续循环
        swap(q[p],q[p/2]),p/=2;//与父节点交换
}

void push(int x)//插入一个元素
{
    q[++tail] = x;//添加元素
    heap_up(tail);//上调
}

操作2:删除操作(pop)

设需要删除的元素下标为\(k\)(当\(k=1\)时，删除的是最小元素)

删除操作的基本流程是:将下标为\(k\)的元素赋值为最后一个元素(\(q[tail]\))，然后删除最后一个元素(\(tail\)--)，最后下调(\(heap\) \(down\))下标为\(k\)的元素。

下调的基本流程:

1. 如果当前节点是叶子节点，结束循环。
2. 比较当前节点与最小的子节点(若没有右子节点，最小的子节点为左子节点)的大小。
   1. 若当前节点比最小的子节点大，交换当前节点与最小子节点的元素，将当前节点的下标\(p\)变为其最小的子节点的下标(\(p\times 2\) 或 \(p\times 2+1\))
   2. 否则(当前节点比最小的子节点小)，结束循环。
3. 继续循环

具体操作演示见 "二叉堆删除操作.pptx"

代码段:

void heap_down(int p)
{
    while(p*2 <= tail)//如果当前节点不是叶子节点
    {
        int tmp;
        if(p*2==tail or cmp(q[p*2],q[p*2+1])) tmp=p*2;
        //如果当前节点只有左子节点或者左子节点比右子节点小
        else tmp=p*2+1;//与左子节点下标交换
        if(cmp(q[tmp],q[p])) swap(q[tmp],q[p]),p=tmp;//否则与右子节点下标交换
        else return ;//如果当前节点比最小的子节点小,结束循环
    }
}

void pop(int k)
{
    q[k] = q[tail];//将需要删除的节点赋值为最后一个元素
    tail--;//删除最后一个元素
    heap_down(k);//下调
}

(六)二叉堆的运用&经典题目

一、堆排序

将元素一个一个地插入堆中，然后一个一个地弹出(取出堆顶元素并删除堆顶元素)，这样得到的序列就是有序的。

时间复杂度: \(O(n\times log_2(n))\)

二、合并果子(题目来源[NOIp2004])

题目传送门 luoguP1090

二叉堆的入门题目

解题思路:运用贪心的思想，每次合并最小的两堆果子。用堆来维护最小值，效率会更高。

三、黑匣子(题目来源[NOI导刊2010提高(6)])

题目传送门 luoguP1801

二叉堆的进阶题目

解题思路:直接按照题目用堆来模拟。因为题目保证\(u\)序列是递增的，所以可以采用对顶堆的维护方式，对于查询第\(i\)大的操作，直接取出最大堆的堆顶，剩下的元素全部放入最小堆中。对于插入操作，保持最大堆中的元素数量为\(i\)，即可。

(七)总结

堆是一种常用的数据结构，在查询极值时有着不俗的表现，时间复杂度为\(O(n\times log_2(n) )\)，常数小，可以优化多种算法，如前文提到过得最短路/最长路算法等等。

优先队列还有一些其他的数据结构，如\(d\)堆、左式堆、斜堆、二项堆、斐波那契堆等，但在信息学竞赛中极少触及，有兴趣可以适当了解，拓宽知识面，增强对“优先队列”的理解。