P11080 [ROI 2019 Day 1] 拍照 题解

题意

给定 \(m\) 个位置和 \(n\) 个颜色，以及一个目标序列。找到一组合法的操作使得一个无色序列能变成目标序列。

• 操作：选定一个颜色 \(c\) 和一个区间 \(l,r\)，将 \(l,r\) 中的每个元素染色为 \(c\)。每个颜色只能用一次，且会覆盖原来的颜色。

思路

首先我们肯定是对一组颜色的左端点到右端点的位置进行染色，这点我们借助图来理解。

在上图中，两条染色区间相交，黑色区间把红色区间的一部分给覆盖了，也就是中间的那一段。而此时红色染右边的一个区间和染右、中两个区间没有区别，所以我们为了简便，只记最后染完（被覆盖后）的左端点与右端点。

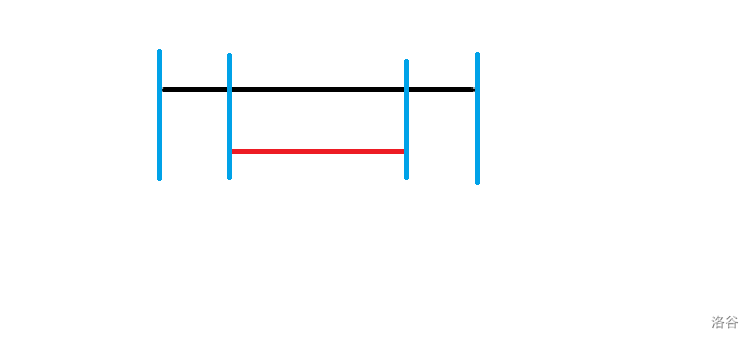
在上图中，黑色区间包含了红色区间，如果黑色区间先染，则红色区间会把黑色区间分为两部分，用因为这两部分必须一起染，所以还是染左端点与右端点之间的区间。

无解

在上面的操作中我们已经得到了一个操作序列，但目标序列可能无解，而我们的操作后的序列是有解（可行）的，此时就要输出 -1。那我们怎么判断呢？很暴力简单，用线段树模拟一遍操作序列，最后在比对目标序列与操作后的序列即可。

Code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5;
int m,n,ans,tot;
int l[N],r[N],a[N],f[N];
struct node{
    int c,l,r;
}Ans[N];
int tree[N*4];
int tag[N*4];
void push_down(int p)
{
    if(tag[p])
    {
        tag[p<<1]+=tag[p];
        tag[p<<1|1]+=tag[p];
        tree[p<<1]+=tag[p];
        tree[p<<1|1]+=tag[p];
        tag[p]=0;
    }
    return ;
}
void push_up(int p)
{tree[p]=tree[p<<1]+tree[p<<1|1];}
void update(int p,int l,int r,int ll,int rr,int v)
{
    if(ll<=l&&r<=rr)
    {
        tree[p]=(r-l+1)*v;
        tag[p]=v;
        return ;
    }
    push_down(p);
    int mid=(l+r)>>1;
    if(ll<=mid)update(p<<1,l,mid,ll,rr,v);
    if(rr>mid)update(p<<1|1,mid+1,r,ll,rr,v);
    push_up(p);
    return ;
}
int get(int p,int l,int r,int to)
{
    if(to==l&&to==r)return tree[p];
    int mid=(l+r)>>1;
    push_down(p);
    if(to<=mid)return get(p<<1,l,mid,to);
    else return get(p<<1|1,mid+1,r,to);
}
bool check()
{
    for(int i=1;i<=tot;i++)
        update(1,1,m,Ans[i].l,Ans[i].r,Ans[i].c);
    for(int i=1;i<=m;i++)
    {
        int now=get(1,1,m,i);
        if(now!=a[i])return false;
    }
    return true;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
	cin>>m>>n;
	for(int i=1;i<=m;i++)
	{
		cin>>a[i];
		if(!l[a[i]])l[a[i]]=i,r[a[i]]=i;
		else r[a[i]]=i;
	}
	int ll,rr;
	ll=rr=0;
	for(int i=1;i<=m;i++)
		if(l[a[i]]==i)
		{
			if(l[a[i]]>rr)
				ll=l[a[i]],rr=r[a[i]];
			else if(r[a[i]]>rr)
				return cout<<-1,0;
            Ans[++tot]=(node){a[i],l[a[i]],r[a[i]]};
		}
    if(!check())return cout<<-1,0;
	cout<<tot;
	for(int i=1;i<=tot;i++)
		cout<<"\n"<<Ans[i].c<<" "<<Ans[i].l<<" "<<Ans[i].r;
	return 0;
}